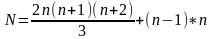50. Сызықтық алгебраның негізгі бөлімдерін атаңыз.

Есептеу математикасында жүйелерді шешу әдістері екі топқа бөлінеді: дәл және итерациялық әдістер.

Дәл әдістер орындалатын амалдар саны санаулы болатын өрнектерден тұрады. Бұл топқа белгілі Крамер формулалары, Гаусс, квадрат түбірлер әдістерін жатқызуға болады. Олар жүйенің дәл шешімін береді. Дәл әдістердің құндылығы есептеу барысында орындалатын арифметикалық амалдардың сандарымен анықталады.

Итерациялық әдістер бір немесе бірнеше параметрлі өзгеріп тұратын алгебралық өрнектерден тұрады. Бұл топқа біртіндеп жуықтау, жәй, Зейдель т.с.с. итерациялық әдістерді жатқызуға болады. Олар жүйенің жуық шешімін тиісті векторлық тізбектердің шегі ретінде анықтайды.

52. Сатж шешудің тіке әдістерін атаңыз.

Дәл әдістер орындалатын амалдар саны санаулы болатын өрнектерден тұрады. Бұл топқа белгілі Крамер формулалары, Гаусс, квадрат түбірлер әдістерін жатқызуға болады.

53. Сатж шешудің итерациялық әдістерін атаңыз.

Итерациялық әдістер бір немесе бірнеше параметрлі өзгеріп тұратын алгебралық өрнектерден тұрады. Бұл топқа біртіндеп жуықтау, жәй, Зейдель т.с.с. итерациялық әдістерді жатқызуға болады

56.Гаусс әдісінің негізгі идеясы неде?

Сызықтық теңдеулер жүйесін шешу үшін кеңінен таралған Гаусс әдісі қолданылады. Бұл әдіс элементарлық түрлендірулерді пайдаланып белгісіздерді біртіндеп жою арқылы теңдеулер жүйесіне алып келуге негізделген.

Элементарлық түрлендірулер:

жүйенің екі теңдеуінің бір-бірімен орын ауыстыруы.

жүйенің теңдеулерінің екі жағын нолге тең емес санға көбейт.

Жүйенің бір теңдеуіне басқа бір теңдеуді нолге тең емес санға көбейтіп қосу.

Түсінікті болу үшін Гаусс әдісінің қарапайым түрін төрт белгісізі бар 4-теңдеулер жүйесі үшін жазып шығайық.

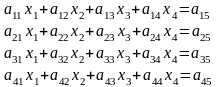(1)

Кейде бос жетекші элемент ретінде матрицаның барлық элементтерінің

ішінен модулі бойынша ең үлкенін алуға да болады. Айталық 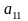жетекші элемент болсын, яғни . -ге бірінші теңдеудің екі жағын бөліп, келесі теңдеуді аламыз.

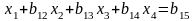(2)

Мұндағы

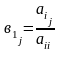
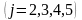
Енді (2)-теңдеуді пайдаланып, 1-ші жүйенің 2-ші, 3-ші, 4-ші теңдеулерінен 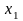белгісізін жоямыз. Ол үшін (2)-ші теңдеуді 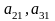және 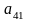-ге көбейтіп 1-ші жүйенің екінші, үшінші, төртінші теңдеулерінен алып тастаймыз. Сонда үш

теңдеуден тұратын төмендегі жүйені аламыз.

( 3) Мұндағы 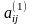-коэффициенттері былай есептеледі

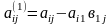
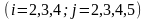(4)

Содан кейін 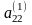жетекші элемент деп алып 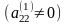(3) жүйенің бірінші теңдеуін осы -ге бөлеміз

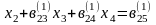(5)

Мұндағы

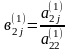
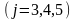
Ары қарай белгісізін жойған тәсілмен, (3) жүйеден белгісізін жойып, екі теңдеуден тұратын жүйе аламыз.

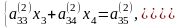(6)

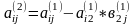
Мұндағы 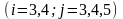(7)

(6) жүйенің 1-ші теңдеуін 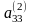бөліп мына теңдеуді аламыз

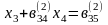(8)

Мұндағы

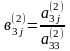
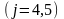
Осы теңдеудің көмегімен (6) жүйенің 2-ші теңдеуінен -белгісізін жоямыз 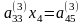(9)

Мұнда 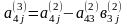(10)

Сонымен (1) теңдеулер жүйесін, оған эквивалентті ұшбұрышты матрицалы теңдеулер жүйесіне келтірдік.

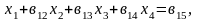
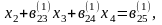(11)

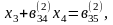
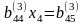
Бұл Гаусс әдісінің тура жолы деп аталады. Енді (11) жүйеден біртіндеп белгісіздерді анықтаймыз.

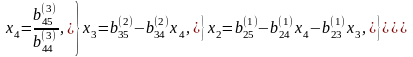(12)

Бұл Гаусс әдісінің кері жолы деп аталады. Бұл Гаусс барлық “жетекші элементтер” нолге тең болмағанда ғана қолданылады. Егер қайсы бір жетекші элемент нолге тең болса, онда ол теңдеуді осы жүйенің жетекші элементі нолге тең болмайтын басқа бір теңдеуімен орын ауыстырамыз.

Бұл айтылғандардың бәрі егер теңдеулер жүйесінің матрицасы ерекше емес болған жағдайда det 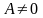ғана орынды.

Гаусс әдісін қолданғандағы, қажетті арифметикалық операциялардың саны, мына формуламен анықталады: