45.Комбинация әдісінің геометриялық интерпретациясын беріңіз.

Хорда және жанамалар әдісі түбірдің жуық мәнін әр түрлі жағынан береді. Сондықтан олардың комбинациясын жиі қолданады және түбірлерді анықтау жылдамырақ болады.

Мейлі теңдеуінің түбірі айырылған және кесіндісінде жатсын.

Егер болса, онда хорда әдісі түбірдің жуықтауын кемімен, ал жанамалар әдісі артығымен береді.

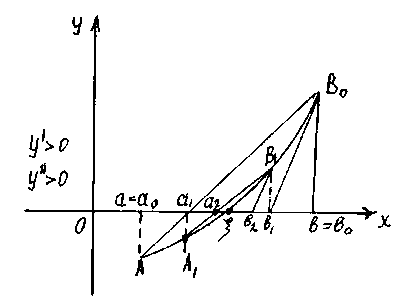
Егер болса, онда хорда әдісімен түбірдің мәнін артығымен, ал жанама әдісімен кемімен табамыз. Бірақ та барлық жағдайда түбірдің шын мәні, хорда және жанама әдісімен алынған жуық мәндердің арасында жатады, яғни мына теңсіздік орындалады , мұнда түбірдің кемімен алынған жуық мәні, артығымен.

Есептеуді былай жүргіземіз. Егер болса, онда ұшы жағынан түбірдің хорда әдісімен алынған жуық мәні, ұшы жағынан жанамалар әдісімен алынған мәні жатады. Онда

, (1)

Енді түбірдің шын мәні интервалында жатады. Осы интервалда әдістердің комбинациясын қолдансақ

,

аламыцз. Ары қарай қолдансақ

, (2)

Егер болса, онда кесіндінің ұшы жағынан жанамалар әдісімен алынған мәні, ал - ұшы жағынан хордалар әдісімен алынған мәні жатады. Сонда

(3)

кесіндісіне әдістердің комбинациясын қолдансақ

,

аламыз. Ары қарай қолдансақ

, (4)

болғанда, есептеу процесі тоқтатылады.

Түбірдің жуық мәні үшін

(5)

қабылданады. және - түбірдің кемімен және артығымен алынған жуық мәні.

46.Итерациялық әдістің жинақтылығының жеткілікті шарты.

Мейлі f(x)=0 теңдеуі берілсін, мұнда f(x) – үздіксіз функция. Осы теңдеудің [a, b] кесіндісінде жататын нақты түбірін табу керек.

f(x)=0 теңдеуін оған эквивалентті

(1)

теңдеуімен алмастырамыз. Алғашқы жуықтау үшін алып

, n=0,1,2,… (2)

тізбегін тұрғизамыз. Бұл тізбек n үмтылғанда кез-келген үшін, (1)-ші теңдеудін [a, b] кесіндісіндегі дәл шешіміне жинакталады. Итерациялық процестің жинақты болуының жеткілікті шартын келтірейік.

Теорема. Мейлі функциясы [a, b] кесіндісінде анықталған, дифференциалданатын және оның барлық мәндері болсын. Бір q саны табылып кесіндісінде <1 болса, онда тізбегі кез-келген үшін, теңдеуінің кесіндісіндісіндегі жалғыз шешіміне жинақталады, яғни

Егер кесіндісінде, оң болса, онда

<

егер теріс болса, онда

<

теңдеуінің дәл шешімі.

Итерациялық процестің бір қадамын жазып көрсетейік. Алдыңғы қадамда табылған мәні үшін, есептейміз. Егер >ε болса, деп болжап келесі итерацияны орындаймыз. Егер <ε болса, есептеуді тоқтатып, түбірдің жуық мәнін деп қабылдаймыз. Алынған нәтиженің қателігі туындының таңбасына байланысты. Егер >0, табылған түбірдің қателігі егер <0 болса, онда қателік ε-нен аспайды.

Әдістің геометриялық интерпретациясы. y=x және функцияларының графиктерін тұрғызамыз. теңдеуінің түбірі ,

қисығының у=х түзуімен қиылысу нүктесінің абсциссасы болады (3-ші сурет). Алғашқы жуықтау үшін кез-келген нүктесін алып, сынық сызықтар тұрғызамыз (3-ші сурет, а, б). Бұл қисықтардың төбелерінің абсциссалары, түбірге жүйелі түрде жақындауды көрсетеді. Егер [a, b] кесіндісінде <0 болса, онда жүйелі түрде жақындау түбірдің маңында шайқалады, ал егер оң болса, онда жүйелі жуықтау тубірге, бірсарынды жақындайды.

Жәй итерация әдісін қолданғанда негізгі мәселе функциясын таңдау болады. Жәй итерация әдісінде функциясын, <1 болатындай етіп таңдау керек. Бұл жағдайда тізбектің түбірге жинақталу жылдамдығы, q саны кіші болған сайын жоғары болады.

Мысал 1. теңдеуінің [0, 1] кесіндісінде орналасқан түбірін итерация әдісімен дәлдікпен тап.

Шешуі. Берілген теңдеуді түріне келтіру керек. Бұны бірнеше әдіспен істеуге болады. Мысалы:

1) онда

2) онда

3) онда

Жүйелі жуықтауларды есептеу үшін алынған функциялардың қайсысын қолдануға болатынын анықтайық. Егер функциясы [a, b] кесіндісінде шартын қанағаттандыратын болса, онда итерациялық процесс жинақты болады. Табамыз

[на 0,1];

на [0,1].

Демек функциясын қолдануға болады және жүйелі жуықтауларды мына формуламен есептейміз

Алғашқы жуықтау үшін [0,1] кесіндісінде максимум мән қабылдайтын нүктені аламыз, яғни (3)-ші формуланы пайдаланып берілген дәлдік орындалу үшін, екі жүйелі жуықтаудың арасындағы айырмашылық қандай болу керек екенін анықтайық:

Сонымен айырымының абсолют шамасы 0,00003 аспаса, итерациялық процесті тоқтатып, берілген дәлдік орындалды деп есептейміз.

Есептеулерді төмендегі кестеде орындаған ыңғайлы:

Осымен итерациялық процесті тоқтатуға болады және деп есептейміз.