36.Дәрежеге шығарудың нәтижесінде қанша мәнді цифр қалдыру керек?
Дәрежеге шығарғанда негізінде қанша мәнді цифр болса сонша мәнді цифрды сақтау керек.
m-ші
дәрежелі түбірдің салыстырмалы қателігі
түбір астындағы санның салыстырмалы
қателігінен m есе кіші.
,
онда
37.Қандай алгоритм орнықты деп аталады?
38.Түбірлерді айыру дегеніміз не және бұл түбірлерді іздеу этапы не үшін қажет?
Кез-келген бір белгісізі бар теңдеуді мынадай түрде көрсетуге болады.
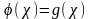(1)
Бір белгісізі бар теңдеуді былай жазуға болады.
(2)
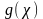функциясын
(1) теңдеудің сол жағына өткізсек оған
тең мынадай теңдеу аламыз
.
Егер осы теңдеудің сол жағын
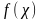деп белгілесек, онда (2) теңдеуді аламыз.
Бұл теңдеудің түбірлерін белгілі бір
формулалармен таба алмаған жағдайда,
онда түбірлерді жуық шамамен табуға
тура келеде. Ол үшін төмендегі екі
мәселені шешу керек:
Ішінде тек бір ғана түбір жататын кішкене облыстарды анықтау. Оны түбірлерді айыру есебі деп атайды.
Берілген дәлдікпен түбірдің жуық мәнін есептеу.
Теңдеудің
түбірлерін графиктік және аналитикалық
әдістермен айыруға болады. Графиктік
әдіс бойынша әуелі
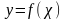функциясының графигі құрылады. Содан
кейін тек бір ғана түбір жататын кішкене
облыстарды графиктің О
осімен қиылысу нүктелерінің обсциссаларын
табу арқылы анықтайды. Кейде
теңдеуін
түбіріне келтіріп,
және
функцияларының графиктерін тұрғызады.
Олардың қиылысу нүктелерінің абсциссалары
теңдеуінің түбірлеріне тең. Сондықтан
жоғарыда айтылған облыстар ретінде
осы абсциссалардың кішкене аймақтары
алынады.
теңдеуінің тек бір ғана түбірі жататын
ең кіші
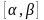аралығын
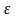дәлдікпен анықтау үшін бисекция әдісі
қолданылады. Оның алгоритмі төмендегідей
болады:
1.
және
нүктелерінде
және
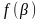мәндері
анықталады; (sign x – сигнум х немесе
х-тің таңбасы);
2.
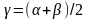нүктеде
мәні
есептеледі;
3.
Егер
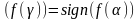болса, онда
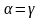деп, ал кері жағдайда
деп алынады;
4.
Егер
болса, онда есептеу 2-ші адымға көшіріледі,
ал кері жағдайда соңғы табылған
және
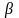сандары тек бір ғана түбір жататын ең
кіші
аралығын анықтайды.
Бисекция алгоритмі баяу жинақталады, бірақ түбірді айыру есебі аяғына дейін шешіледі.
Ол үшін математикалық талдау курсынан белгілі, функциялардың кейбір қасиеттерін пайдаланамыз.
Теорема
1. Егер үздіксіз
функциясы
кесіндісінің ұштарында әр түрлі таңбалы
мәндер қабылдаса, онда осы
кесіндісінің ішінде
теңдеуінің ең болмағанда бір түбірі
болады.
Теорема 2. Егер функциясы кесіндісінде монотонды және үздіксіз болса және кесіндінің ұштарында әр түрлі таңбалы мәндер қабылдаса, онда осы кесіндінің ішінде теңдеуінің тек бір ғана түбірі болады.
Теорема
3. Егер
функциясы
кесіндісінде үздіксіз және кесіндінің
ұштарында әр түрлі таңбалы мәндер
қабылдаса, ал туындысының
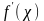осы кесіндінің ішінде таңбасы өзгермейтін
болса, онда
кесіндісінің ішінде
теңдеуінің түбірі болады және ол біреу
болады.
Аналитикалық әдіспен түбірді былай айыруға болады:
Бірінші туындыны табамыз.
2. - ті туындының критикалық мәніне не шекаралық мәнге тең деп болжап,
функциясының таңбасының кестесін құрамыз.
3. Ұштарында функция қарама-қарсы таңбалы мәндер қабылдайтын интервалдарды анықтаймыз. Бұл интервалдардың ішінде тек бір ғана түбірден болады.
39.k –еселі түбір дегеніміз не?
Берілген [a,b] кесіндісінде түбірдің бар болуының шартын жазыңыз.