25. Основные задачи диагностики технических объектов и систем управления (см. 26 вопрос)

26. Структура типовой системы диагностики

Диагностика технического объекта (ТО) – это оценка текущего состояния объекта и сравнение его с эталонными состояниями.

Процедура диагностики предполагает решение задач классификации.

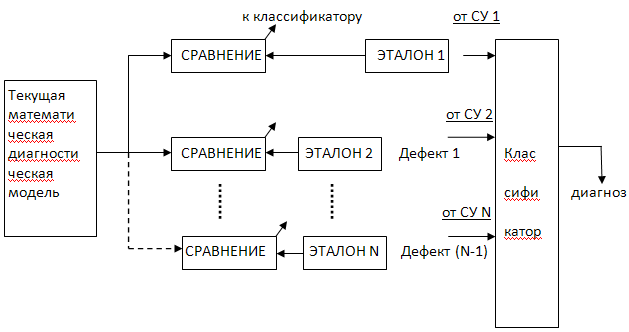
ЭТАЛОН 1 – бездефектное состояние модели (эталон 1 должен быть в любой модели)

Последующие эталоны характеризуют наличие какого-либо дефекта.

Отказы бывают перемежающиеся и постоянные.

Еще одна задача диагностики оценка ресурсов (нужно оценить вероятностную бездефектную работу объекта).

На этом этапе разработки ОУ констр. расчет на основании опыта расчетных данных; определяются самые слабые узлы объекта. В этом случае СД должна отслеживать состояние именно этих узлов. Системы диагностики разделяются на 2 группы: 1. предполагает использование текстовых диагностических сигналов (это, как правило, при стендовых испытаниях) 2. предполагает оценку текущего состояния объекта в режиме его нормального функционирования.

27. Распределение задачи диагностики по уровням

вы

28. Применение пространственно-временных спектральных преобразований при построении диагностических моделей

Вектор диагностических признаков представляет собой математическую модель.

П араметры должны быть связаны с состоянием объекта.

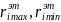
Параметры диагностической модели получены исходя из измеряемых сигналов.

– вектор входных возбуждающих сигналов

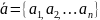– вектор, характеризующий параметры объекта, который необходимо контролировать

Решение задачи диагностики:

Зависимость состояния a1, a2 ... не зависит от r.

Уравневое решение задачи диагностики.

В теории решение представляется на 3-х уровнях:

Отсутствие / наличие дефекта.

Локализация места дефекта.

Определение места, входа дефекта и его характеристика (т.е. размер)

Эти 3 уровня могут быть выполнены 2-мя способами:

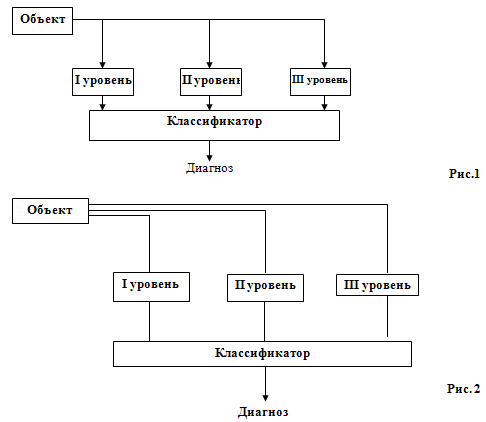
На рис.1 поступает на I, II, III уровни одинаковая информация.

Решение задачи I уровня более простое в отличие от II и III, работают в режиме реального времени.

На рис.2 для I, II, III уровней поступает различная информация как по объему, так и по содержанию. Решают в одном и том же режиме реального времени. Рис.2 более специализированная структура.

Использование пространственно-временных спектров для решения задачи диагностики.

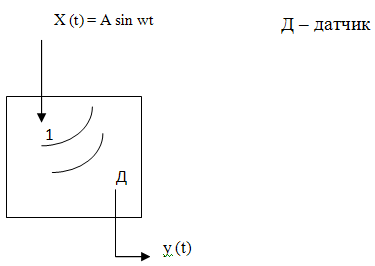
В 1 поступает механический сигнал с амплитудой А.

При наличии трещины информация, содержащаяся в сигнале, будет значительно отличаться от сигнала, где не трещины.

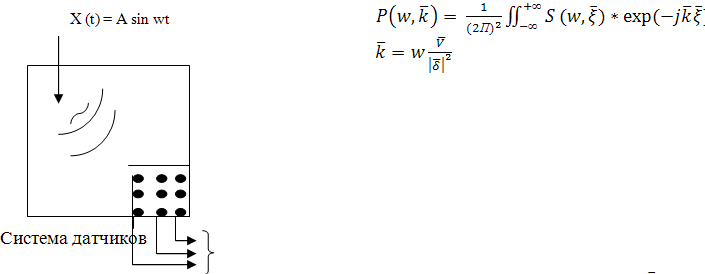
Если имеется система датчиков, то место расположения датчиков определяется

– волновое число обратное скорости распространения в среде

– скорость распределений

P – пространственно-временной спектр

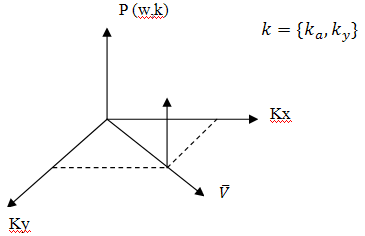
определяется если соединить точки находящиеся на плоскости чисел и началом координат.

Можем определить, откуда идет сигнал, т.е. можем определить, где находится дефект.

Если в 1 поступает сигнал из набора сумм гармонических колебаний, то спектр будет выглядеть так:

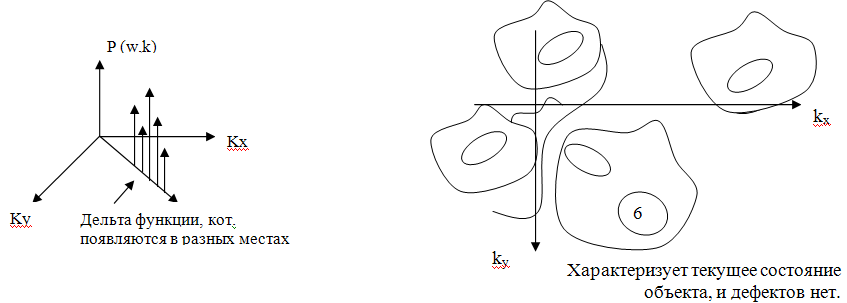
В случае дефекта числа могут меняться, вершины могут дрейфовать, и могут появляться новые вершины.