
- •1. Применение метода наименьших квадратов при экспериментальном определении статических характеристик объектов управления. (ответ на вопрос построение…)
- •2. Применение полного факторного эксперимента при определении статических характеристик объектов управления.
- •3. Применение дробного факторного эксперимента при определении статических характеристик объектов управления
- •4. Рандомизация и разбиение матрицы на блоки при использовании факторных экспериментов при определении статических характеристик объектов управления
- •10. Интерпретация результатов, полученных при экспериментальном определении частотных характеристик динамического объекта
- •11. Определение динамических характеристик линейных объектов при апериодических воздействиях
- •12. Обработка результатов эксперимента по снятию переходных функций
- •13. Определение частотных характеристик объектов управления по переходным функциям
- •14. Основное уравнение статистической идентификации (уравнение Винера-Хопфа)
- •15. Алгебраический метод решения уравнения статистической идентификации (уравнения Винера-Хопфа)
- •16. Регуляризация решения уравнения статистической идентификации (уравнения Винера-Хопфа)
- •17. Решение уравнения статистической идентификации (уравнения Винера-Хопфа) с помощью электронной модели
- •18. Частотный метод решения уравнения статистической идентификации (уравнения Винера-Хопфа)
- •19. Использование уравнения статистической идентификации (уравнения Винера-Хопфа) при идентификации функционирующего объекта
- •20. Использование уравнения статистической идентификации (уравнения Винера-Хопфа) при идентификации объекта, охваченного обратной связью
- •25. Основные задачи диагностики технических объектов и систем управления (см. 26 вопрос)
- •26. Структура типовой системы диагностики
- •27. Распределение задачи диагностики по уровням
- •28. Применение пространственно-временных спектральных преобразований при построении диагностических моделей
17. Решение уравнения статистической идентификации (уравнения Винера-Хопфа) с помощью электронной модели
вы
18. Частотный метод решения уравнения статистической идентификации (уравнения Винера-Хопфа)
Исп. тогда, когда объект явл. нестационарным, а вл. сигнал явл. стационарным






С учетом полученного результата запишем:


Умножаем под интегральную функцию на 1:


Учитывая что частотном ПФ нестационарного объекта представляет из себя:

Выражение -//- !!!сопряженная частотная хар-ка нестационарного объекта
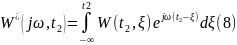


Тогда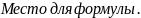

Выражение (11) это взаимная спектральная плотность


Если объект был бы стац-ым,то:

19. Использование уравнения статистической идентификации (уравнения Винера-Хопфа) при идентификации функционирующего объекта
n (t)-случайный сигнал («БШ» достаточно близкий к беному нуму)
K nn(t)=Co б(t) (1)
Co-интенсивность «БШ»
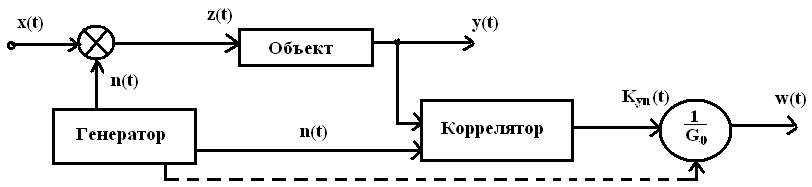

Переведем выражение (2) от сигналов к их хар-ам.

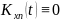 учитывая что статист. связи мех x и n
нет. Тогда:
учитывая что статист. связи мех x и n
нет. Тогда:

Подставим (1) в (4)

Учитывая фильтрующее свойство ∆ функций получим :

Тогда следует
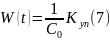
20. Использование уравнения статистической идентификации (уравнения Винера-Хопфа) при идентификации объекта, охваченного обратной связью
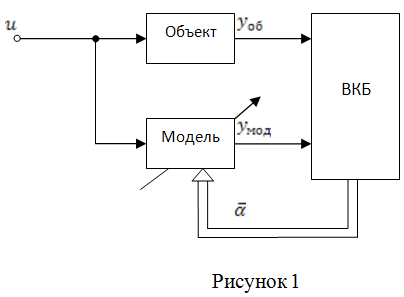
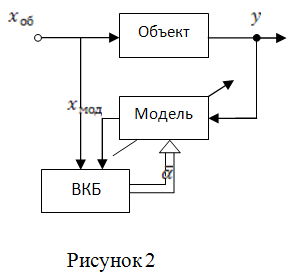
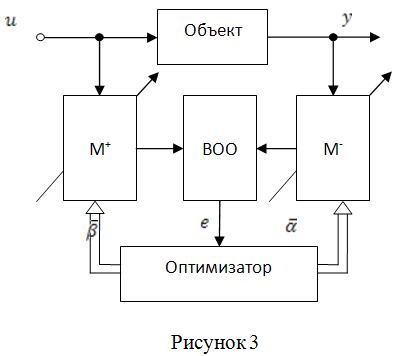
ВКБ – вычислитель критерия близости
ВОО – вычислитель обобщенной ошибки
Рисунок 1 – прямая настраиваемая модель
Параметры – вектор

Рисунок 2 – обратная модель
Рисунок 3 – обобщенная модель
(Рисунок 1 и Рисунок 2)
M+ M-
Выходы используются для вычисления
ошибки

Алгоритм использования моделей:
Выбор структуры модели
Выбор критерия

Выбор алгоритма поиска
 (экстремального критерия)
(экстремального критерия)
21. Методы идентификации с использованием настраиваемых моделей, виды моделей
вы
22. Использование структурной модели при идентификации объектов управления


 (1)
(1)

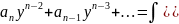
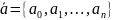
Пространство параметров:
 ,
,

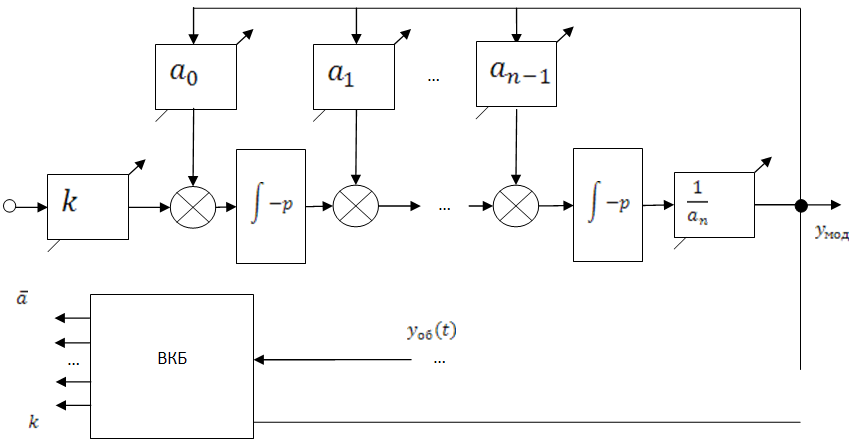
23. Применение обобщенной модели Эйкхоффа для параметрической идентификации объектов управления


 (1)
(1)

 (2)
(2)
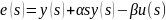 (3)
(3)

 (4)
(4)
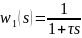 (5)
(5)
 (6)
(6)

Во временной области:
 (7)
(7)
 (8)
(8)
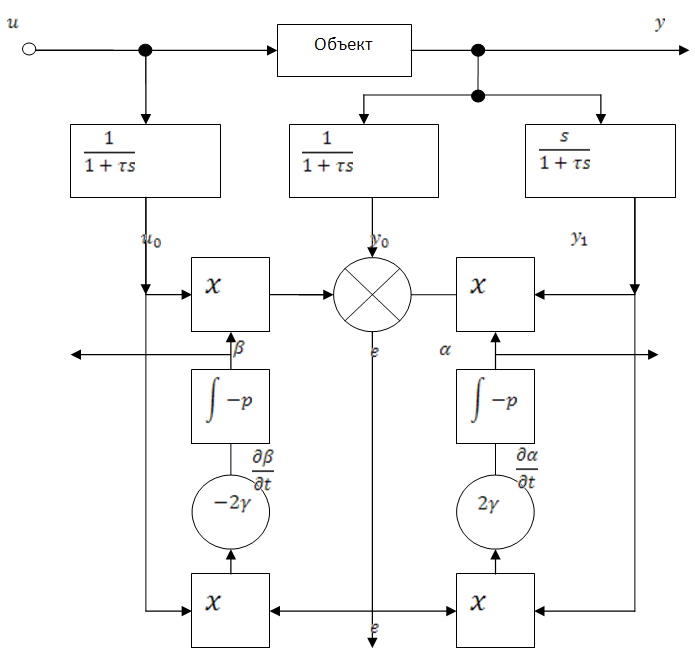
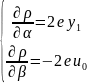 (9)
(9)
 ;
;
 (10)
(10)
 (11)
(11)
 (12)
(12)


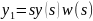
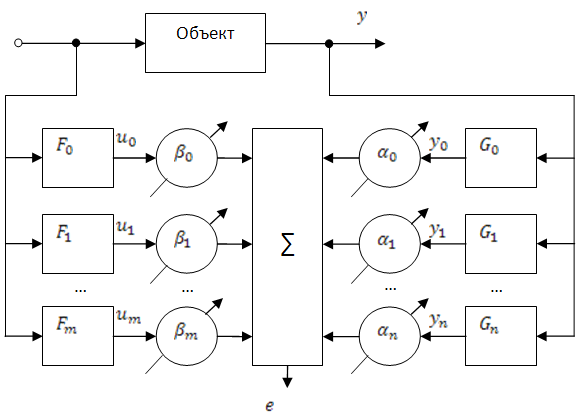
24. Использование ортогональных фильтров для построения настраиваемых моделей
hi(t) – импульсные переходные функции ортоганальных фильтров;
zi – выходной сигнал фильтров.
z =

где z – выходной сигнал сумматора
ρ = M{[y-z]2}
где ρ – критерий настройки, М – математическое ожидание
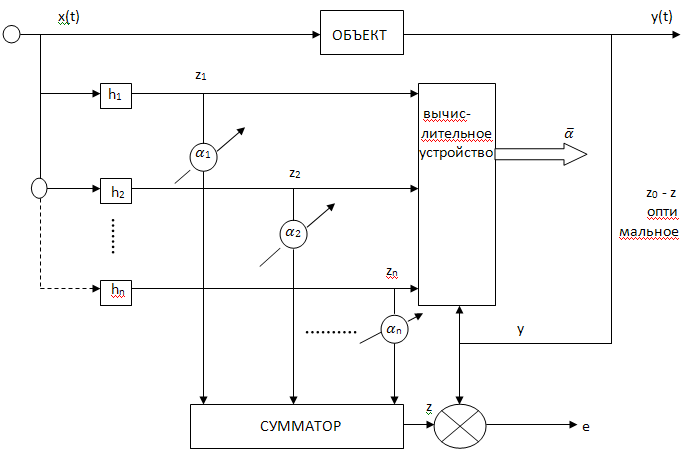
Допустим мы нашли min ρ:
min ρ: zopt = z0 =
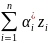
где
 - результат настройки модели (модель
это весь рисунок, кроме объекта)
- результат настройки модели (модель
это весь рисунок, кроме объекта)
Умножим выражение (3) на величину zj обе части:
M {z0zj} =
 M {zjzi}
M {zjzi}
это уравнение в сокращенном виде:
(4а) B = K𝛼
где B – вектор столбец, содержащий взаимокорреляционную функцию
Kz0zj (0); Kzizj (0)
 =
=
 M {[ y2 – 2yz + z2]} = M {[ y2 – 2y
M {[ y2 – 2yz + z2]} = M {[ y2 – 2y
 zi + (
zi + (
 zi )2]}
zi )2]}
-2M {yzi} + 2M {z0zj} = 0
M {yzj} = M {z0zj}
Kyzj (0) = Kz0zj (0)
Выражение (8) позволяет заменить нам в выражении (4) корреляционные функции
ошибка (e) чисто информационная
