10. Интерпретация результатов, полученных при экспериментальном определении частотных характеристик динамического объекта
вы
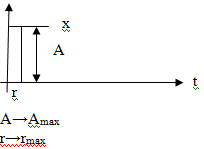
11. Определение динамических характеристик линейных объектов при апериодических воздействиях
x(t)=δ(t)
y(t)≈W(t) ИПФ
W(s)=L{W(t)}
W(s)=∫от 0 до ∞ W(t) e-st dt (*)
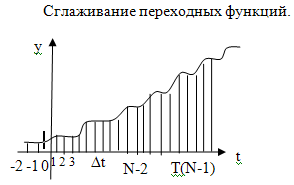
1 - ∆t
2 - 2∆t
3 - 3∆t
…
…
…
N-2 – (N-2) ∆t
N-1 – (N-1) ∆t
n(t) – помеха, приведенная к выходу
M{n(t)}=0 математическая динамика помехи
y(0)=y0
y(∆t)=y1
y(2∆t)=2y2
…
y[(N-1) ∆t]=yN-1
y[(N-2) ∆t]=yN-2
Алгоритм «скользящего среднего»
Интервал разбивается на число нечетное отрезков
Вычисляется среднее число ординат функции (у находится на этом интервале и это значение приписывается середине интервала)
Затем интервал сдвигается на отрезок ∆t и процедура повторяется.
Для определения
нужно
изменить функция до скачка
l=4
Развитием метода является метод, который предложил Ланцори
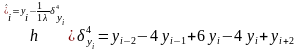
Макс вес от той координаты, которой даем оценку.
12. Обработка результатов эксперимента по снятию переходных функций
вы
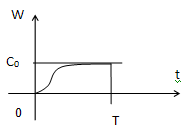
13. Определение частотных характеристик объектов управления по переходным функциям
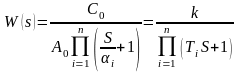(2) где А0-амплитуда входного сигнала
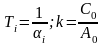
(3)
(4)
(5)
(6)
по полученной функции строим график проведем прямую аппроксимирующую линию
Уравнение (6) является уравнением прямой линии.
(7)
(8)
(9)
14. Основное уравнение статистической идентификации (уравнение Винера-Хопфа)
Объект-нестационарный;входные,выходные сигналы-нестационарные
Уравнение свертки y(t)=
(1)
Уравнение математического ожидания my(t)=
(2)
Запишем выражения для взаимной корреляционной функции между аналогами входа и на входе.
Ky,x(t1,t2)=
(3)
M – математическое ожидание
Подставим (3) в соотв. значение (1) и (2) и получим
Kyx(t1,t2) =
(4)
Kyx(t1,t2)=
(5)
-
Kyx(t1,t2)=
(6)
Если момент начала функционирования объекта и момент начала наблюдения за объектом совпадают,то в уравнение (6)
Kyx(t1,t2)=
Если объект обладает конечной памятью Т,то уравнение (6)
Kyx(t1,t2)=
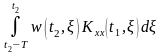
Если объект явл. нестационарным,а входной стационарным,то (6)
Kyx(t1,t2)=
Если объект явл. стационарным и входной сигнал явл. стационарным,то уравнение
Kyx(t1,t2)=
15. Алгебраический метод решения уравнения статистической идентификации (уравнения Винера-Хопфа)
Этот метод применяется тогда, когда объект и входной сигнал стационарны.
Kyx(t)= (1)
Kyx(t)≈
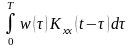(2)
I Этап T= Tyx
II Этап перейдем от ∫ к ∑
Kyx(t)=
(3)
t=
,
j=0, N-1 См *
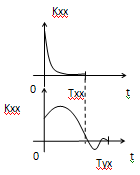
Tyx > Txx
Kxx(t)=Kxx(-t) –корреляционная функция
Kyx(t)≠Kyx(-t) –взаимно-корреляционная функция
* j=0
j=1
…
j=N-1
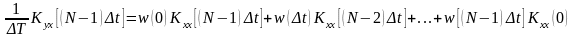
16. Регуляризация решения уравнения статистической идентификации (уравнения Винера-Хопфа)
Уравнение относится к неккоректным по Абелю задачам.
Эта некорректность проявляется в следующем:
При малых вариациях этого члена(Kyx) и подинтегральном выражением (Kxx) мы можем получать решение данного уравнения (W(t)) (ИПФ)с погрешностями как количеством так и качественнымими значительного отличающ. от вариаций Kyx и Kxx.
2 Подхода регуляции:
Регуляризация по Тихонову.
Закл. в том, что на основе уравнения Винера-Хопфа строится функционал, содержащий нек. дол. коэф-ты и осущ. минимизация этого функционала, в результате чего получается регуляризационное решение.
Регуляризация по Грабарь. Метод Грабарь
(2) n=0,N
{φ} имеется некий набор функций φ, которые представляют собой базис
Что означает следующее свойство: Функции являются ортоноримированны
Исп.этих функции для разложения и синтеза имп. реш-он функции.
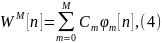
где
M<<N
Где
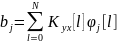
Подставим в (2) выражение (4) и (5)
Умножим обе части (6) на
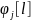и
Т.о. уравнение (7):
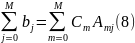
Решаем уравнение (8) получаем Сm и подставляем в (4).
Тем самым получаем регуляризованное выражение.