
- •1. Применение метода наименьших квадратов при экспериментальном определении статических характеристик объектов управления. (ответ на вопрос построение…)
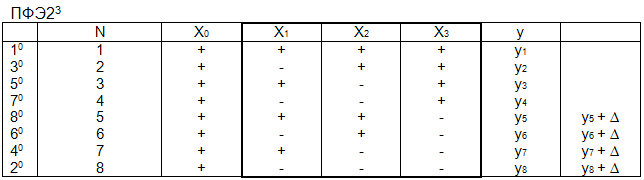
- •2. Применение полного факторного эксперимента при определении статических характеристик объектов управления.
- •3. Применение дробного факторного эксперимента при определении статических характеристик объектов управления
- •4. Рандомизация и разбиение матрицы на блоки при использовании факторных экспериментов при определении статических характеристик объектов управления
- •10. Интерпретация результатов, полученных при экспериментальном определении частотных характеристик динамического объекта
- •11. Определение динамических характеристик линейных объектов при апериодических воздействиях
- •12. Обработка результатов эксперимента по снятию переходных функций
- •13. Определение частотных характеристик объектов управления по переходным функциям
- •14. Основное уравнение статистической идентификации (уравнение Винера-Хопфа)
- •15. Алгебраический метод решения уравнения статистической идентификации (уравнения Винера-Хопфа)
- •16. Регуляризация решения уравнения статистической идентификации (уравнения Винера-Хопфа)
- •17. Решение уравнения статистической идентификации (уравнения Винера-Хопфа) с помощью электронной модели
- •18. Частотный метод решения уравнения статистической идентификации (уравнения Винера-Хопфа)
- •19. Использование уравнения статистической идентификации (уравнения Винера-Хопфа) при идентификации функционирующего объекта
- •20. Использование уравнения статистической идентификации (уравнения Винера-Хопфа) при идентификации объекта, охваченного обратной связью
- •25. Основные задачи диагностики технических объектов и систем управления (см. 26 вопрос)
- •26. Структура типовой системы диагностики
- •27. Распределение задачи диагностики по уровням
- •28. Применение пространственно-временных спектральных преобразований при построении диагностических моделей
3. Применение дробного факторного эксперимента при определении статических характеристик объектов управления
Использование ДФЭ2к-р возможно, если имеются степени свободы.
y = b0x0 + b1x2 + … + bkxk + b12x1x2 + … + b1234x1x2x3x4
Если в уравнении (1) отсутствуют возможные 2,3-ные и более высокого порядка взаимодействия, то имеется соответственное число степеней свободы.
При проведении ДФЭ2к-р при наличии соотв. степеней свободы выбирются генерирующие соответствия (Р), тогда общее число эксперимента N = 2к-р.
y = b0x0 + b1x1 + b2x2 + b3x3 + b4x4 + b5x5
x4 = x1 x3
x5 = x1 x2 x3 – произведение столбцов в матрице

ДФЭ25-2
x1, x2, x3, x4, x5
x4 = x1 x2 x5 = x1 x2 x3 (1)
x4 = x1 x3 x5 = x1 x2 x3 (2)
x4 = x2 x3 x5 = x1 x2 x3 (3)
x4 = -x1 x2 x5 = x1 x2 x3 (4)
x4 = -x1 x3 x5 = x1 x2 x3 (5)
x4 = -x2 x3 x5 = x1 x2 x3 (6)
x4 = x1 x2 x5 = -x1 x2 x3 (7)
x4 = x1 x3 x5 = -x1 x2 x3 (8)
x4 = x2 x3 x5 = -x1 x2 x3 (9)
x4 = -x1 x2 x5 = -x1 x2 x3 (10)
x4 = -x1 x3 x5 = -x1 x2 x3 (11)
x4 = -x2 x3 x5 = -x1 x2 x3 (12)
Определяющий контраст (ОК) –представляет из себя набор столбцов одного знака, исключая столбец фиктивной координаты Х0.
x4 = x1x3 x5 = x1x2 x3
ОК1 = x1 x3 x4
ОК2 = x1 x2 x3 x5
ОК3 = x2 x4 x5 ОК3 = ОК1 * ОК2
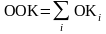 -
обобщающий определяющий контраст
-
обобщающий определяющий контраст
х42 = х4 х4 = х4 х1 х3 = +1
ОК3 = x12 x2 x32 x4 x5
+1 +1
С помощью ООК выявляются эффекты смешивания.
y = b0x0 + b1x1 + b2x2 + b3x3 + b4x4 + b5x5 (*)
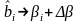

βi – истинное значение коэф.
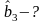
ООК * х3 = x1 x4 + x1 x2 x5 + x2 x3 x4 x5 (**)
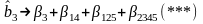
4. Рандомизация и разбиение матрицы на блоки при использовании факторных экспериментов при определении статических характеристик объектов управления
Рандомизация – порядок проведения эксперимента определяется случайным образом.
В начале составляется матрица по двоичному правилу, включая генератор случайных чисел.
3, 18, 47, 67, 51, 22, 74, … (64 эксперимента)
Эксперимент табл.
№1 3
№2 18
№3 47
№4 51
№5 22
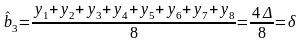 -
дополнительная ошибка
-
дополнительная ошибка
При проведении ПФЭ и ДФЭ в начале составляется исходная матрица, затем разбивается на блоки, т.о., чтобы в каждом блоке количество «+» и «-» было одинаковое. В каждом блоке проводится процедура рандомизации.
5. Учёт динамики объекта при определении статических характеристик в режиме пассивного эксперимента
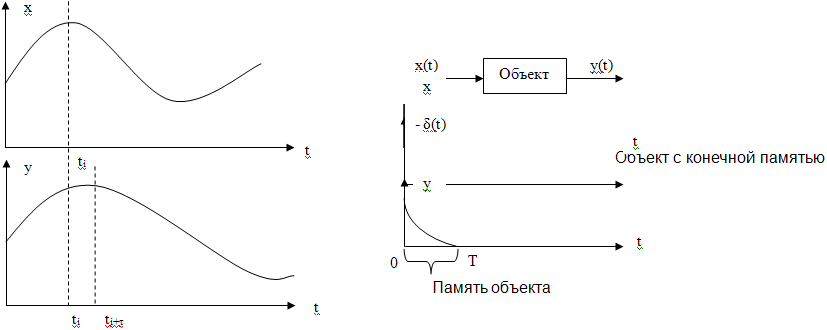
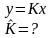
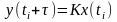 (1)
(1)
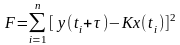 (2)
(2)
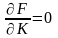 (3)
(3)
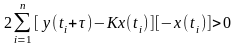 (4)
(4)
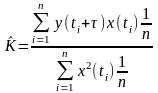 (5)
- Взаимная корреляционная функция
(5)
- Взаимная корреляционная функция
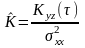 (6)
- дисперсия
(6)
- дисперсия
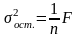 (7)
(7)
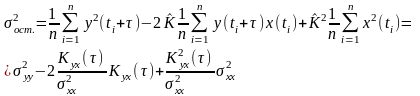 (8)
(8)
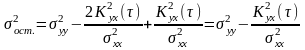 (9)
(9)
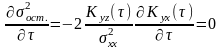 (10)
(10)
(10) справедливо если: а)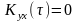 -
не может быть;
-
не может быть;
б)
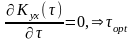
Алгоритм:
Определяем взаимную корреляционную функцию Кух.
Находим производную Кух.
6. Экспериментальные методы исследования объектов управления при периодических воздействиях
вы
7. Предварительное изучение объекта исследования
вы
8. Определение частотных характеристик объекта управления с использованием гармонических анализаторов
Коэффициенты Фурьеk-ая симфазная
гармоника (1)
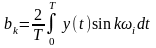 T=mTi
, m=1,2,3,…
T=mTi
, m=1,2,3,…
k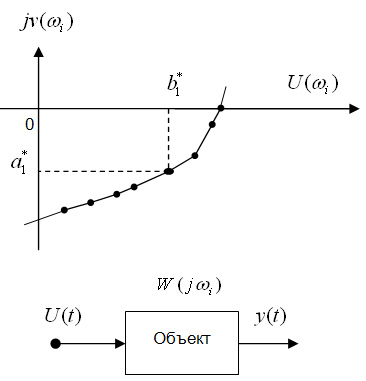 -ая
квадратурная гармоника (2)
-ая
квадратурная гармоника (2)
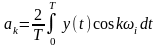
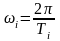 ,
k=1,2,3,…
,
k=1,2,3,…
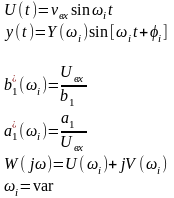
Соединяем полученное, получаем АЧХ

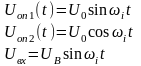
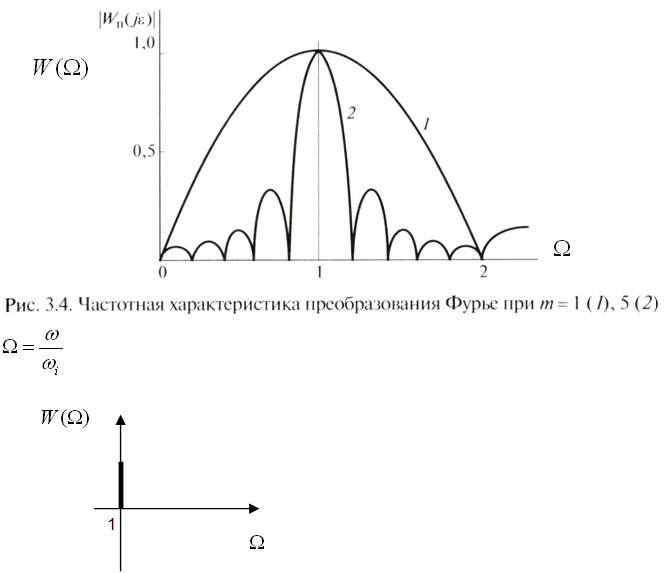
Время интегрирования д.б. кратное числу сигналов.
Основные частоты проходят без искажения, не давятся.
Если Т=Т1, то ЧХ=1.
Кроме основного сигнала, она пропускает частоты до того и после того момента.
При увеличении периодов ЧХ фильтра приближается к идеальному фильтру.
Возможны проблемы на инфранизких частотах.
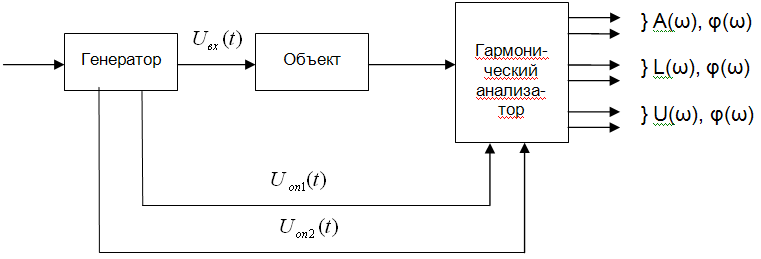
9. Проведение эксперимента по определению частотных характеристик объекта управления с использованием гармонических анализаторов (Структурные схемы экспериментального определения частотных характеристик)
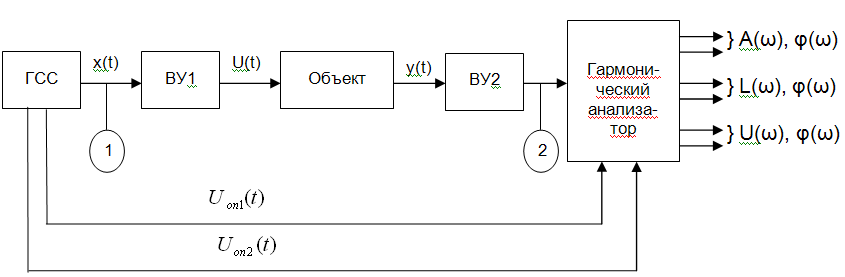
X(t)=Xm sin ωt 
U(t)=Um sin ωt (*) 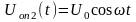 ω=var
ω=var
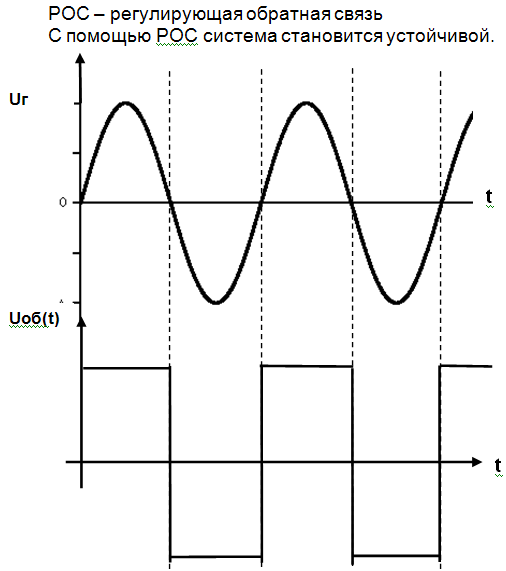
Y(t)=Ym sin (ωt +φ(ω))
Uоб(t)= Uоб sin (ωt +φ(ω))
ВУ1, ВУ2 – вспомогательное устройство
ГСС – генератор синусоидных сигналов
ВУ – преобразователь мощности, изменение диапазона напряжения
В уравнении (*) возможен фазовый сдвиг.
ВУ1 – преобразователь сигнала из электрической формы в другую форму, т.о. преобразователь и согласователь сигнала.
ВУ2 – набор разных датчиков, которые преобразуют электрическую форму.
Может происходить усиление сигнала (изменение диапазона).
1
Выход
2
Вход
На выходе гармонический анализатор посчитает ЧХ между точками 1 и 2
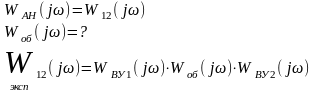
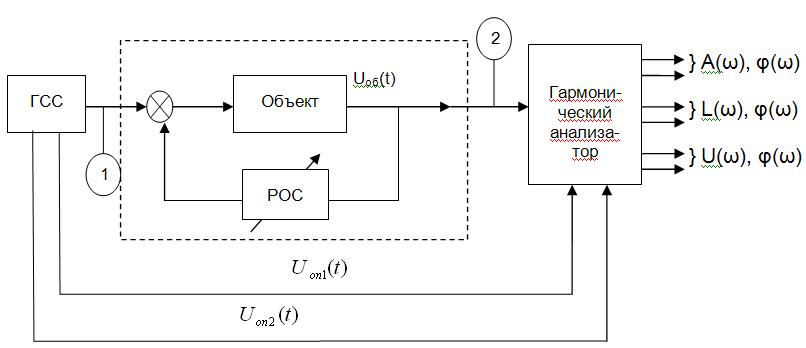
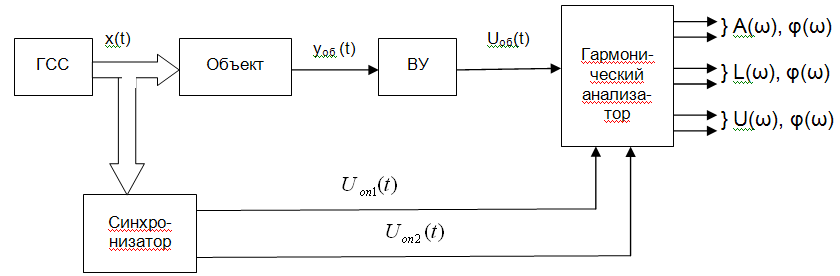
Выше приведенная структура определения ЧХ, применяется, когда объект очень инерционный.
x(t)=Xm sin ωt
UОП1(t)= U0 sin ωt
UОП2(t)= U0 cos ωt
На синхронизатор поступает механический сигнал.
