1. Применение метода наименьших квадратов при экспериментальном определении статических характеристик объектов управления. (ответ на вопрос построение…)

Пусть априори мы имеем дело с линейным объектом. y=b₀+b₁x Наклон определяется как tgα.

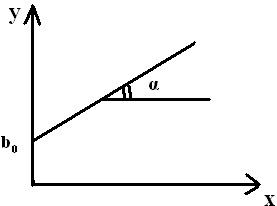
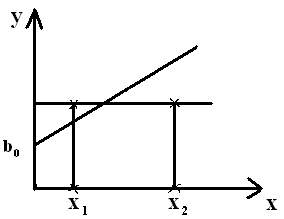Т.к есть помехи по факту

b₀ - ? b₁ -?

Введем фиктивную координату х₀ =1, х=х₁, получим.

y=b₀+b₁x (1)

y=b₀+b₁x₁ (2)

y=b₀x_0i+b_ix_1i , где i=1..N (3) это некорректное равенство.

e_i=y_i-b₀x_0i-b_ix_1i (4) помеха

МНК: (5)

, (6)

(7)

(8)

= (9)

Пусть для реальных объектов имеет координаты x₁

y=b₀x₀+b₁x₁+ b₂x₂+ …b_кx_{к .} Т. е. характеристика в пространстве [x_1… x_k]

=

Метод можно так же использовать для нелинейных зависимостей.

y=b₀x_α

ln y=ln b₀ = α lnx

w= b₀ + b₁ x переход в линейную область.

w=ln y

B₀=ln b₀

b₁ =α

2. Применение полного факторного эксперимента при определении статических характеристик объектов управления.

Д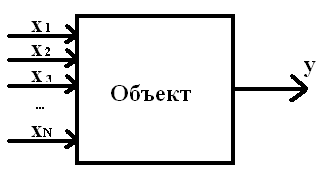 опустим имеется всего 5 координат: х₁ х₂ х₃ х₄ х₅ . Каждому параметру будем давать всего 5 значений. Тогда количество экспериментов нужно провести N=5⁵=3125

х_1, х₂ … х_k – факторы (входные сигналы)

у – функция отклика

Чтобы провести факторный эксперимент:

1. Нужно чтобы все факторы были управляемы (их можно изменить по желанию экспериментатора).

2. Факторы должны быть измеряемы с требуемой точностью.

3. Факторы должны быть совместимы (по технологическим условиям все забранные значения факторов разрешены). Т.е. подавать на вход можно только то, что разрешено.

При проведении ПФК2^к каждый из факторов принимает только 2 значения.

П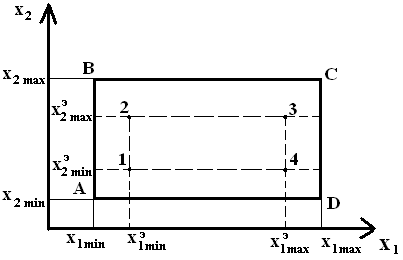 роведение эксперимента:

АВСД – область варьирования факторов. (определяются min и max каждого фактора, т.е. ТУ).

Внутри АВСД определяются значения факторов, которые задаются в процессе проведения эксперимента.

Точки 1, 2, 3, 4 – это экспериментальные min и max, они могут быть только в АВСД, но не за ней и не на границе.

-1 («-») – min^э значение факторов

+1 («-») – max^э значение факторов

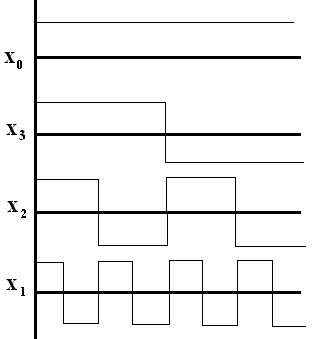
Составим матрицу планирования: ПФК2³ (т. е. 3 фактора) N=2³=8 экспериментов

y=b₀x₀ +b₁x₁+b₂x₂+b₃x₃ (x₀=1 фиктивный столбец)

№	x0	x1	x2	x3	x1x3	y
1	+	+	+	+	+	y1
2	+	-	+	+	-	y2
3	+	+	-	+	+	y3
4	+	-	-	+	-	y4
5	+	+	+	-	-	y5
6	+	-	+	-	+	y6
7	+	+	-	-	-	y7
8	+	-	-	-	+	y8

Свойства:

1. Свойство симметричности: =0, i=1...k

2. Свойство нормировки: 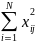=N, i=1...k

3. Свойство ортогональности: , i=1...k, p=1...k, i≠p

4. Свойство рототабельности (т. е. все точки эксперимента равноправны в статистическом смысле).

Делаем оценку коэффициентов:

= = =

= , i=0...k

Метод можно применять и для линейных функций.

y=b₀x₀ +b₁x₁+b₂x₂+b₃x₃+ b₁₃ x₁x₃ =