Теоретическая температура горения

Достижению калориметрической температуры препятству­ет прежде всего то, что СО₂ и Н₂О — продукты горения всякого топлива, независимо от его исходного состояния — являются сложными химическими соединениями, разлагающимися при высоких температурах. Этот процесс диссоциации продуктов сгорания, количественно иллюстрируемый уравнениями

2СО₂ 2СО + О₂— 136440 ккал (77)

2Н₂О 2Н₂ + О₂ — 115 620 ккал, (78)

по существу является обратным процессу горения окиси угле­рода СО и водорода Н₂. Таким образом, основные реакции го­рения суть обратимые реакции, для которых, как и для всяких химических реакций, между отдельными составными частями фазы или их физико-химическими характеристиками устанавли­вается некоторая зависимость, определяемая величиной так на­зываемой константы равновесия.

Для интересующих нас процессов диссоциации СО₂ и Н₂О эти константы равновесия определяют величину отношений пар­циальных давлений исходных веществ и продуктов диссоциа­ции. Для реакции диссоциации угольного ангидрида постоянная равновесия выражается следующим образом:

(79)

и для диссоциации водяного пара:

(80)

Величина постоянной равновесия зависит от температуры; теоретически эта зависимость определяется формулой Вант-Гоффа, практически же приходится пользоваться эмпириче­скими формулами, построенными по типу выражения, получае­мого при интегрировании формулы Вант-Гоффа.

Для диссоциации СО₂ формула Саккура устанавливает сле­дующую зависимость постоянной равновесия от температуры:

(81)

Для водяного пара:

(82)

Если в качестве меры диссоциации принять отношение ко­личества распавшегося вещества к количеству первоначального взятого (так называемый коэффициент диссоциации), то мож­но легко установить связь между константой равновесия и ко­эффициентом диссоциации.

Если обозначить:

а —коэффициент диссоциации СО₂ или Н₂О;

— число молей избыточного кислорода на 1 моль диссоци­ирующего газа;

z —число молей газов, не принимающих участия в реакции, отнесенное к 1 молю диссоциирующего газа;

Р — общее давление системы, то

(85)

Для диссоциации чистых СО₂ и Н₂О в условиях, когда v = 0 и z= 0, имеем:

(84)

Последние уравнения в сочетании с предыдущими зависи­мостями от Т дают уравнения равновесия, при помощи кото­рых устанавливается связь между коэффициентом диссоциации

и температурой.

Так как в результате диссоциации в продуктах сгорания по­являются СО и Н₂ наряду со свободным кислородом, то естест­венно, что количество сообщенного продуктам сгорания тепла меньше величины теплотворности топлива на величину теплоты трения продуктов диссоциации СО и Н₂. В результате темпера­тура горения, определенная с учетом диссоциации, будет ниже температуры, определяемой без учета этого явления.

Температуру, до которой могут быть нагреты продукты сго­рания топлива при частичной диссоциации угольного ангидри­да и водяного пара, условимся называть теоретической темпе­ратурой горения. Эта температура всегда ниже калориметриче­ской. Теоретическая температура в большей или меньшей степени приближается к калориметрической. Из уравнений для опре­деления константы равновесия следует, что с повышением темпе­ратуры константа равновесия уменьшается; следовательно, уменьшается парциальное давление недиссоциировавшей дву­окиси углерода и водяного пара. В результате расхождение между калориметрической температурой, определяемой в пред­положении, что диссоциация отсутствует, и теоретической, учи­тывающей ее влияние, увеличивается. Если при определении температуры продуктов сгорания исходить из равенства

(85).

то влияние диссоциации скажется и в уменьшении Q и в изме­нении m. Обе эти величины зависят от степени диссоциации, т. е. от величины а — коэффициента диссоциации. Так как в уравне­нии равновесия и в уравнении калориметрическом величины а и t одни и те же, то для определения теоретической температуры горения получаются два уравнения с двумя неизвестными — температурой и коэффициентом диссоциации.

Наиболее просто решение этой системы достигается графи­чески— путем отыскания координат точки пересечения двух кривых, построенных для каждого из уравнений. Первая кри­вая характеризует зависимость температуры от степени диссо­циации; вторая дает зависимость коэффициента диссоциации от температуры.

Задача решается в следующем порядке. Задаваясь различ­ными значениями коэффициента диссоциации, определяют со­ответствующую данному значению коэффициента диссоциации температуру продуктов сгорания. По полученным точкам стро­ят в осях а —t кривую. Затем, задаваясь значениями темпера­тур, определяют из уравнения равновесия значения коэффици­ентов диссоциации. На той же сетке наносят новые данные. Пе­ресечение двух кривых дает значения t и а, удовлетворяющие обоим уравнениям.

Такой метод решения предложен акад. Н С. Курнаковым [14] и рекомендуется проф. Б. В. Старком как единственно возможный для случая, когда в продуктах сгорания присутст­вуют одновременно СО₂, Н₂О и О₂.

Иллюстрируем примером этот метод определения теорети­ческой температуры, используя некоторые данные из предыду­щего расчета горения бензола.

В указанном расчете были определены:

1. начальное теплосодержание продукта сгорания io = 900 ккал/нм³,

2)состав продуктов сгорания, если диссоциация отсутствует.

3) калориметрическая температура горения =2219 .

% Доли

СО, 16,1 0,161

Н₂О 8,1 0,081

N₂ 75,8 0,758

100,0 100,0

Для определения теоретической температуры необходимо учитывать, что в продуктах сгорания одновременно присутству­ют СО₂ и Н₂О, так что должно установиться равновесие между пятью составными частями:

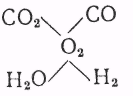
Следовательно, при решении задачи необходимо учитывать наличие трех неизвестных — температуры t _m, коэффициента диссоциации СО₂ — х и коэффициента диссоциации Н₂О — у. Трем неизвестным соответствуют и три уравнения:

Последнее уравнение можно заменить новым, получающим­ся путем вычитания второго из третьего и деления полученного равенства на 2,

Левая часть этого равенства не что иное, как логарифм пос­тоянной равновесия реакции

СО+Н₂О = СО₂ + Н₂

Значение этой постоянной, как и логарифмов постоянных и приведены в табл. 33.

Состав продуктов горения при диссоциации СО₂ и Н₂О выразится сле­дующим образом:

СО₂ 0,161 (1-х) =0,161—0,101 х

СО……………0,161 х =0,161 х

Н₂О 0,081 (1— у) . . =0,031—0,081 у

Н₂ 0,081 у =0,081 у

О_{2…………………..}0,5-0,161 x+0,5-0,081 у =0,08х + 0,04 у

N_{2…………………….}0,758 =0,758

Σ=1,0+0,08х+0,04у

В свою очередь объемная теплоемкость водяного пара ниже теплоемкости двуокиси углерода. Теплоемкость двуокиси угле­рода, водяного пара, азота и других газов возрастает с повыше­нием температуры; при этом наиболее быстро с повышением температуры возрастает теплоемкость двуокиси углерода. Теп­лоемкость водяного пара и особенно теплоемкость азота и дру­гих двухатомных газов возрастает с повышением температуры значительно медленнее. Так, средняя теплоемкость двуокиси углерода в температурном интервале от 0 до 2000° в 1,55 раза больше теплоемкости при 0°; средняя теплоемкость водяного пара в данном температурном интервале в 1,30 раза больше теплоемкости при 0°, а теплоемкость азота в интервале темпе­ратур от 0 до 2000° только в 1,15 раза превышает теплоемкость при 0°

Средняя теплоёмкость газов от до t , по Юсти

t	СО2	Н2О	воздух	N2	О2	Н2	СО	SО2	СH4	C2 H4	t
0 100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100 2200 2300 2400 2500 2600 2700	0.384 0.409 0.431 0.449 0.464 0.480 0.492 0.503 0.513 0.522 0.530 0.538 0.544 0.550 0.556 0.561 0.565 0.569 0.573 0.577 0.580 0.583 0.586 0.589 0.591 0.593 0.595 0.597	0.356 0.358 0.362 0.367 0.372 0.378 0.384 0.390 0.397 0.403 0.410 0.416 0.422 0.427 0.433 0.439 0.444 0.450 0.455 0.460 0.464 0.469 0.473 0.478 0.481 0.485 0.489 0.492	0.310 0.311 0.318 0.315 0.318 0.321 0.324 0.328 0.331 0.334 0.337 0.340 0.343 0.345 0.347 0.350 0.352 0.354 0.355 0.357 0.358 0.359 0.360 0.362 0.363 0.365 0.366 0.367	0.310 0.311 0.312 0.314 0.316 0.319 0.322 0.324 0.327 0.331 0.334 0.337 0.340 0.342 0.345 0.347 0.349 0.351 0.353 0.354 0.356 0.357 0.359 0.360 0.362 0.363 0.364 0.365	0.312 0.314 0.319 0.324 0.329 0.334 0.339 0.343 0.347 0.350 0.355 0.356 0.359 0.362 0.364 0.366 0.368 0.370 0.372 0.374 0.376 0.377 0.379 0.380 0.382 0.383 0.385 0.386	0.306 0.309 0.310 0.311 0.311 0.312 0.313 0.314 0.315 0.316 0.318 0.319 0.321 0.323 0.325 0.327 0.328 0.330 0.332 0.334 0.336 0.338 0.340 0.342 0.343 0.345 0.347 0.349	0.310 0.311 0.312 0.315 0.318 0.321 0.324 0.328 0.332 0.335 0.338 0.341 0.344 0.346 0.348 0.350 0.352 0.354 0.356 0.358 0.359 0.361 0.362 0.364 0.365 0.366 0.368 0.369	0.415 0.435 0.453 0.469 0.484 0.496 0.506 0.515 0.523 0.530 0.536 0.541 0.546 0.550 0.554 0.557 0.560 0.563 0.565 0.567 0.570 0.572 0.573 0.575 0.577 0.578 0.580 0.581	0.368 0.386 0.419. 0.451. 0.480 0.509 0.537 0.563 0.588 0.610 0.632 - - - - - - - - - - - - - - - - -	0.447 0.503 0.556 0.605 0.650 0.691 0.729 0.762 0.799 0.824 0.851 - - - - - - - - - - - - - - - - -	0 100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100 2200 2300 2400 2500 2600 2700

Однако несмотря на столь значительное различие в значе­ниях теплоемкостей СО₂, Н₂О и N₂, теплоемкости продуктов сго­рания углерода и водорода в стехиометрическом объеме воздуха близки между собой на всем температурном интервале от 0 до 2100. Малое различие в теплоемкости продуктов сгорания углерода и водорода в воздухе объясняется тем, что при горении углерода по уравнению

С + О₂ + 3,76N₂ = СО₂ + 3,76 N₂

_{Средняя теплоёмкость газов от до t ,}

t	СО2	Н2О	N2	О2	воздух	СО	Н2	СH4	C2 H6	C2 H4
0 100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100 2200 2300 2400 2500	0.3821 0.4061 0.4269 0.4449 0.4609 0.4750 0.4875 0.4988 0.5090 0.5181 0.5263 0.5338 0.5407 0.5469 0.5526 0.5578 0.5626 0.5671 0.5712 0.5750 0.5785 0.5818 0.5848 0.5876 0.5902 0.5926	0.3569 0.3595 0.3636 0.3684 0.3739 0.3797 0.3857 0.3920 0.3984 0.4050 0.4115 0.4180 0.4244 0.4306 0.4366 0.4425 0.4481 0.4537 0.4589 0.4639 0.4686 0.4735 0.4779 0.4822 0.4864 0.4903	0.3092 0.3095 0.3104 0.3121 0.3144 0.3161 0.3201 0.3233 0.3265 0.3295 0.3324 0.3352 0.3378 0.3404. 0.3427 0.3449 0.3470 0.3490 0.3508 0.3525 0.3541 0.3557 0.3571 0.3585 0.3598 0.3610	0.3119 0.3147 0.3189 0.3239 0.3290 0.3339 0.3384 0.3426 0.3463 0.3498 0.3529 0.3557 0.3584 0.3608 0.3631 0.3653 0.3673 0.3693 0.3712 0.3730 0.3748 0.3764 0.3781 0.3797 0.3813 0.3828	0.3098 0.3106 0.3122 0.3146 0.3174 0.3207 0.3240 0.3274 0.3306 0.3338 0.3367 0.3395 0.3422 0.3447 0.3470 0.3492 0.3513 0.3532 0.3551 0.3568 0.3585 0.3600 0.3615 0.3629 0.3643 0.3655	0.3103 0.3109 0.3122 0.3145 0.3174 0.3207 0.3242 0.3277 0.3311 0.3343 0.3374 0.3403 0.3430 0.3455 0.3479 0.3501 0.3522 0.3541 0.3559 0.3576 0.3592 0.3607 0.3621 0.3634 0.3647 0.3659	0.3049 0.3083 0.3098 0.3103 0.3110 0.3117 0.3124 0.3134 0.3145 0.3159 0.3174 0.3191 0.3208 0.3227 0.3246 0.3266 0.3285 0.3304 0.3324 0.3343 0.3362 0.3388 0.3398 0.3416 0.3433 0.3451	0.3702 0.3922 0.4201 0.4505 0.4814 0.5112 0.5400 0.5677 0.5957 0.6216 0.6447 0.6655 0.6838	0.5278 0.5959 0.6627 0.7271 0.7902 0.8485 0.9023 0.9521 0.9986 01.0418 1.0818 1.1187 1.1525	0.4363 0.4925 0.5452 0.5960 0.6415 0.6839 0.7227 0.7571 0.7901 0.8196 0.8472 0.8731 0.8963

Значение постоянной К₃ и логарифмов постоянный К₁ и К₂

Температура t, 0C	Lg K1 (2CO2  2H2+O2)	Lg K2 (2H2O 2H2+O2)	K3 (CO+H2O= =CO2+H2)	Температура t, 0C	Lg K1 (2CO22CO2+O2)	Lg K2 (2H2O 2H2+O2)	K3 (CO+H2O= =CO2+H2)
1000 1100 1200 1300 1400 1500 1600 1700	13,975 12,220 10,696 9,363 8,185 7,134 6,204 5,347	14,557 13,044 11,732 10,606 9,564 8,659 7,846 7,113	1,871 2,095 2,420 2,820 3,240 3,620 4,220 4,621	1800 1900 2000 2100 2200 2300 2400 2500	4,578 3,878 3,236 2,648 2,105 1,602 1,135 0,701	6,448 5,842 5,287 4,777 4,306 3,870 3,465 3,089	5,039 5,481 5,970 6,522 7,160 7,918 8,835 9,961

Cледовательно,

K₁ = ,

K₁ = .

K₃ = ,

K₃ = .

Отсюда

y = .

Задаёмся температурой равновесия 2000, для которой

lg K₁ = 3,236 и K₃ = 5,970

Принимаем x = 0,180, тогда

y =

lg K₁ = lg ,

lg K₁ = lg = lg 1335,0 = 3,1260,

Принимаем x = 0,16, тогда

y = = 0,032,

lg K₁ = lg = lg 1999,0 = 3,2990

Для интерполяции находим:

3,299 – 3,126 = 0,173

3,236 – 3,126 = 0,110

0,173 : 0,02 = 0,110 : s,

откуда

s = = 0,126

х = 0,18 – 0,0126 = 0,1674

у = = 0,0325

Находим температуру, соответствующую

х = 0,1674 и у = 0,0325

Состав продуктов горения:

м³ %

СО₂ 0,161 (1-0,1674) . . . . . . . . . . . . . . . . . . . . . . . . . = 0,1338 13,75

СО 0,161 0,1174 . . . . . . . . . . . . . . . . . . . . . . . . . . . = 0,0280 2,76

Н₂О 0,081 (1- 0,0325) . . . . . . . . . . . . . . . . . . . . . . . . = 0,0783 7,70

Н₂ 0,081  0,0325 . . . . . . . . . . . . . . . . . . . . . . . . . . . = 0,027 0,27

О₂ 0,5  0,161  0,1674 + 0,5  0,081  0,0325 . . . . = 0,017 1,67

N₂ 0,758 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .= 0,758 74,45

 = 1,0178 100,00

Тепло для нагрева продуктов сгорания:

горение бензола. . . . . ккал

диссоциация СО₂ . . . . - 3045 0,0280 = - 84

Н₂О. . . . – 2580 0,0027= - 7

793 ккал

Теплосодержание i^ продуктов сгорания при t^ = 2000 .

СО₂ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,1315  1159 = 152,2 ккал

СО . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,0276  718,4 = 19,9 »

Н₂О . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,0770  929,0 = 71,6 »

Н₂ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,0027  672,0 = 1,8 »

О₂ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,0167  751,5 = 12,5 »

N₂ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,7445  712,2 = 531,0 »

i^ = 789.0 ккал/м³

Теплосодержание i^ продуктов сгорания t^ = 2100

СО₂ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,1315  1224 = 166,0 ккал

СО . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,0276  758,1 = 20,9 »

Н₂О . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,0770  985,8 = 76,0 »

Н₂ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,0027  709,4 = 1,9 »

О₂ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,0167  791,8 = 13,2 »

N₂ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,7445  750,6 = 559,5 »

i^ = 837,5 ккал/м

t = 2000+  100 = 2000 + 8 = 2008.

Так как температура получилась выше 2000 , то искомая температура выше 2000 и ниже 2100.

Задаёмся температурой равновесия 2100. Для этой температуры

lg K₁ = 2,648

K₃ = 6,522.

Принимаем х = 0,240, тогда

y = = 0,046

lg K₁ = lg ( ) = 2,689

Принимаем х = 0,250, тогда

y = = 0,049,

lg K₁ = lg   = 2,622

2,689 – 2,622 = 0,067

2,648 – 2,622 = 0,026

0,067  0,01 = 0,026  s,

откуда

s = = 0,0039

х = 0,25 – 0,0039 = 0,2461,

у = = 0,0475.