Рекомендуемые значения зубцового деления статора при прямоугольных пазах

таблица 3

Полюсное деление , м	0,15	0,15-0,4	0,4
Зубцовое деление t1,m	0,017-0,022	0,017-0,022	0,020-0,028

Рекомендуемые значения зубцового статора при позакрытых пазах

таблица 4

Число полюсов, 2р	2	4	6	8
Зубцовое деление t1, мм	10+(0,2-0,05)	10+(0,015-0,025)	10+0,03	10+0,07

Примечание:  в мм.

Ky₁=sin (19)

Ky_y =sinv (20)

где v- порядок высшей гармоники.

Коэффициенты распределения обмоток при целом q соответственно равны

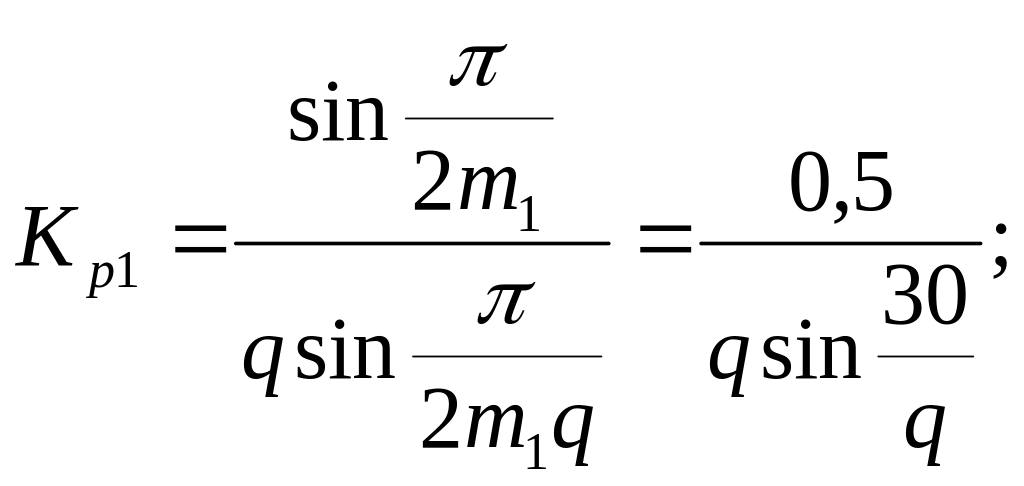(21)

(22)

Обмоточный коэффициент первой гармоники равен произведению

K_ob1=K_y1K_p1 (23)

Соответственно обмоточный коэффициент высшей гармоники равен

K_obv=K_yvK_pv (24)

В расчете обмотки необходимо привести кроме обмоточных коэффициентов первой , пятой и седьмой гармоник значение этих коэффициентов для двух первых зубцовых гармоник, порядок которых определяется оп формуле

v₃=(Z₁/p)K±1 (25)

при К=1.

В двигателях малой мощности и в двигателях малошумного исполнения для у меньшения высших гармоник м.д.с. и особенно гармоник зубцового порядка применяются скос пазов статора или ротора. Коэффициент скоса, учитывающий снижение м.д.с., рассчитывается по формуле

Κ_ск≈(sinγ_CK/2)/0,5γ_CK (26)

где γ_CK≈(v₃₁b_CK   - угол скоса;

b_ck - величина скоса.

При расчете _ck полюсное деление  и величину скоса b_ck нужно брать в одних линейных размерах ( например , в мм).

Обычно скос выполняют на роторе примерно равным одному зубцовому делению (рис.5) . В этом случае для первой гармоники K_ck , а для гармоник зубцового порядка он значительно меньше единицы , что приводит к уменьшению амплитуды высших гармоник м.д.м., снижению величины потерь и уровня шума двигателя.

Число последовательно соединенных витков фазы обмотки статора можно определить из уравнения электрического равновесия

E₁=U_K_E=4,44f₁W₁K_ob1_m (27)

откуда

W₁= U_K_E/(4,44f₁K_ob1_m) (28)

где

_m=(2/__ (29)

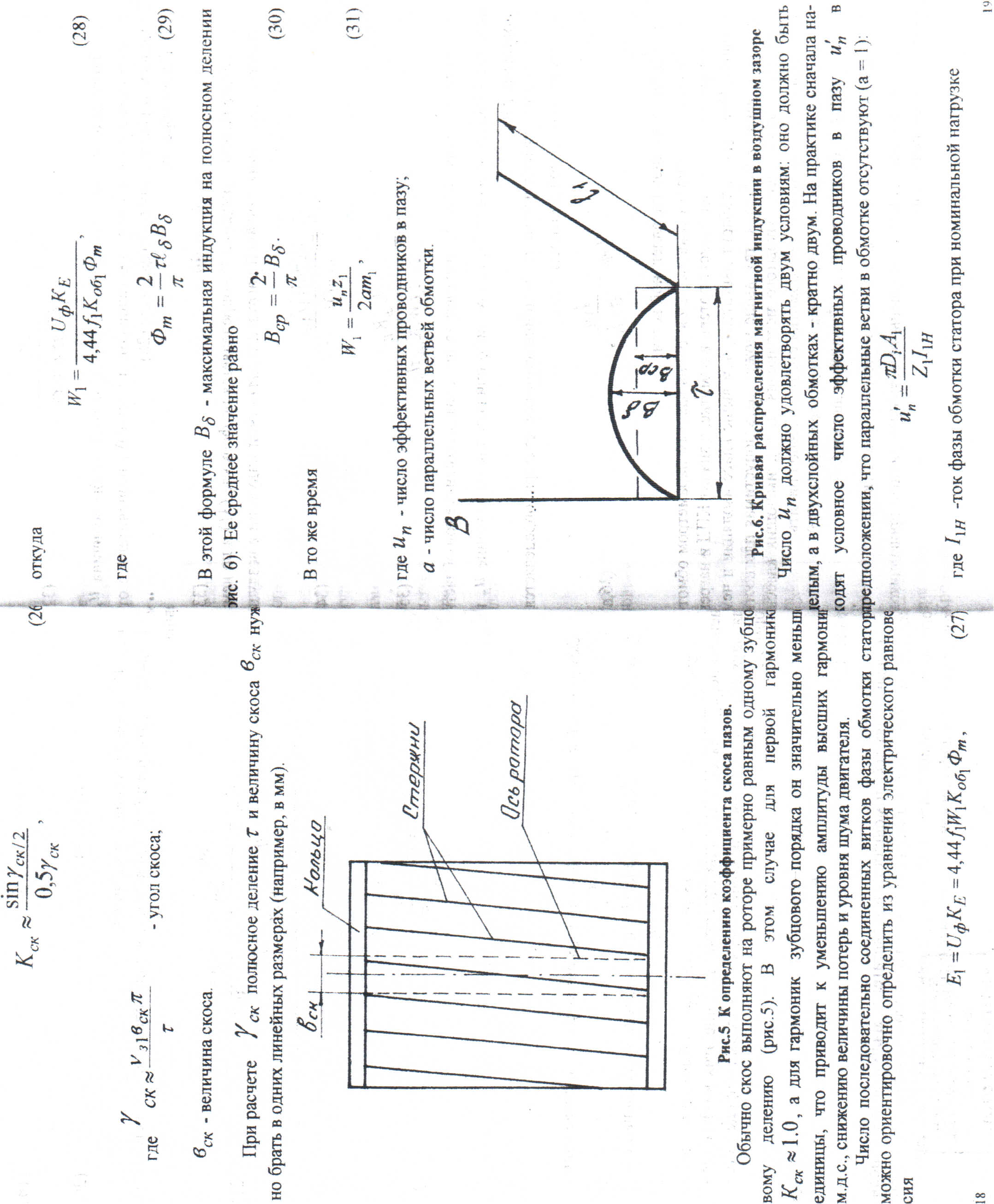
Рис.5 К определению коэффициента скоса пазов.

В этой формуле _ - максимальная индукция на полюсном делении (рис.6).Ее среднее значение равно

B_cp=(2/_ (30)

В то же время

W₁=(u_nz₁)/(2am₁) (31)

где u_n – число эффективных проводников в пазу;

1. число параллельных ветвей обмотки

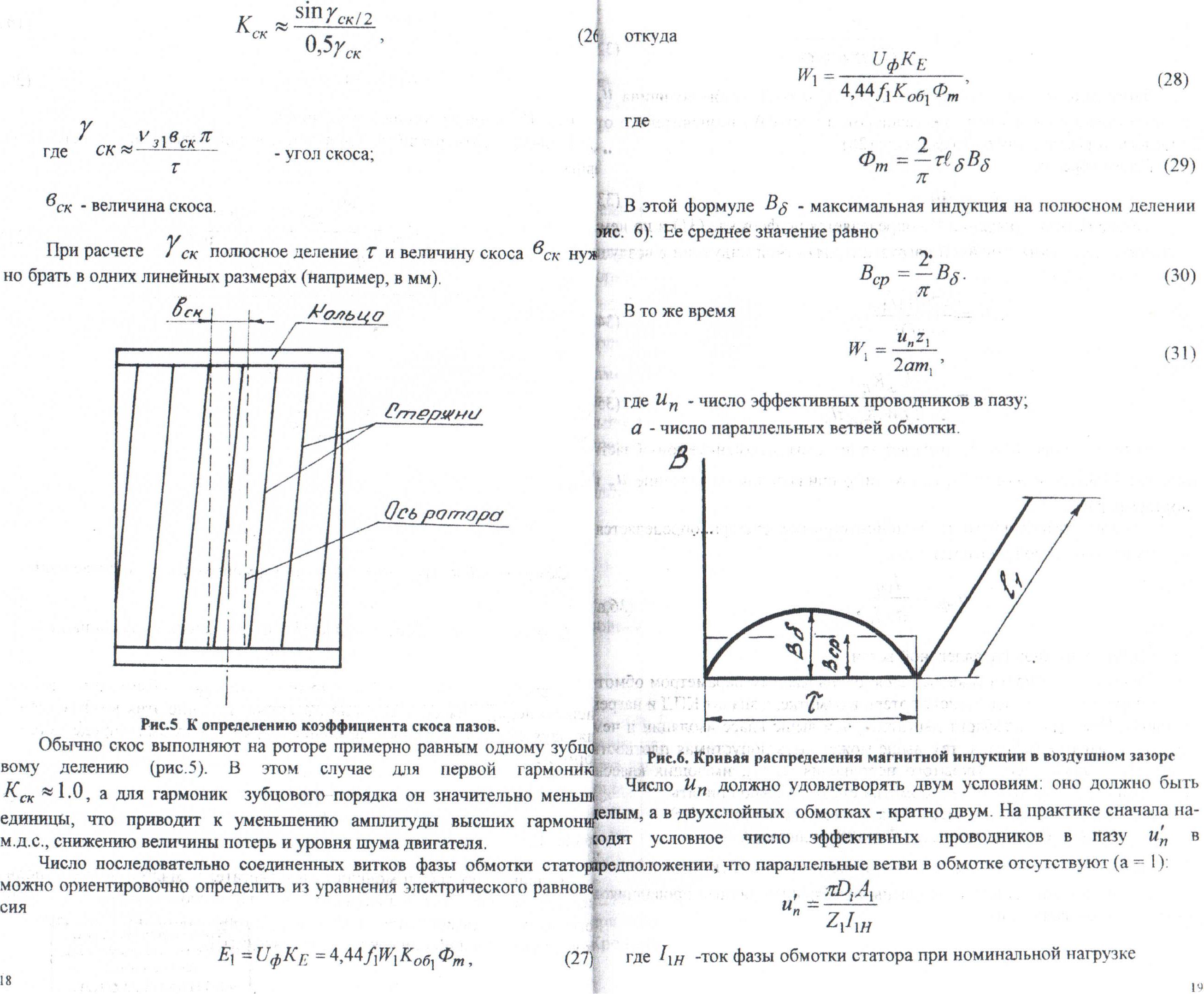
Рис.6 Кривая распределения магнитной индукции в воздушном зазоре

Число u_n должно удовлетворять двум условиям : оно должно быть целым, а в двухслойных обмотках- кратно двум. На практике сначала находят условное число эффективных проводников в пазу u_n^’ в предположении, что параллельные ветви в обмотке отсутствуют (а=1):

u_n^’=D_iA₁)/(Z₁I_1H)

Где I_1H - ток фазы обмотки статора при номинальной нагрузке.

I_1H=P₂/(m₁U__Hcos_H) (32)

Затем находят такое число параллельных ветвей, чтобы величина удовлетворяла названным выше условиям, а число W1 незначительно отличалось от рассчитанного по формуле (28)

Таким образом,

u_n=a u_n^’ (33)

Окончательное значение W1 определяется по формуле (31) и по ней уточняются значения линейной нагрузки и магнитной индукции в воздушном зазоре

A₁=(2 m₁W₁ I_1H)/D_i) (34)

_U__√f₁W₁K_ob1_ (35)

Если значения A1 и _ выходят за пределы рекомендуемой области (см.рис.1) более , чем на 5 %, необходимо принять другое значение u_n повторить расчет.

Сечение эффективного проводника обмотки статора определяется исходя из допустимой плотности тока j₁ , т.е.

q_эф1= I_1H/(a*j₁) (36,а)

где I_1H/a -ток одной параллельной ветви.

Величина плотности тока является очень важным параметром обмотки статора . так как от нее зависят потери в обмотке, чем выше класс изоляции и чем лучше условия охлаждения, тем выше может быть допустимая плотность тока. Для двигателей закрытого исполнения (IP44), имеющих класс изоляции F и H, плотность тока обмотки статора можно принять

j₁ =7-9 А/мм² - для двигателей малой мощности (до 10кВт)

j₁ =6-8 А/мм² – для двигателей большей мощности.

Исходя из величины q_эф1, в зависимости от конструктивного исполнения обмотки могут быть определены обмоточные данные проводников статора 9 (приложения 2 и 3 ).

Для всыпных обмоток применяется обмоточный провод диаметром не более 1,4-1,8мм с сечением 1,5-2,5мм². Если расчетное сечение q_эф1 по равенству (36,а) выше указанных значений, то подбирается несколько элементарных проводников такого диаметра, чтобы их суммарное сечение было близко к расчетному

q_эл n_эл= q_эф1 (36,б)

Число элементарных проводников должно быть не более 5-6 , а при механизированной укладке – не более 2-3. В случае , если такого количества элементарных проводников недостаточно, увеличивают число параллельных ветвей. Исключение составляют двухполюсные двигатели , у которых число параллельных ветвей а=1.

В двигателях большой мощности с прямоугольными пазами и с обмоткой статора из проводников прямоугольного сечения один проводник должен иметь сечение не более 17-20 мм², т.к. при больших сечениях заметно возрастают потери на вихревые токи. В случае, если q_єф1>17-20 мм². Выбор размеров прямоугольного провода производится после расчета зубцовой зоны и пазов.

Расчет обмоточных даннях фазы статора заканчивается уточнением плотности тока по выбранным значениям q_эл, n_эл и  .

j= I_1H/(a q_эл n_эл) (37)

С определением площади паза статора, необходимой для размещения проводников фазы

S_n’=( q_эл n_элu_n)/K_M (38)

где к_м=0,4-0,45 – ориентировочные значения коэффициента заполнения паза медью учитывает, что 55-60 % площади поперечного сечения паза занято пазовой и проводниковой изоляцией и пропиточными компаундами.