29.Методы интегрирования:метод разложения,метод замены переменной.

1) ∫f1(x)+f2(x)dx=∫f1(x)dx+∫f2(x)dx

2) ∫Cf(x)dx=C∫f(x)dx

3) Если ∫f(x)dx=F(x)+C ,то ∫f(u)du =F(u)+C , где u=φ(x)

I. ∫λ₁f₁(x)+…+λ_nf_n(x)dx= λ₁∫f₁(x)dx+ λ_n∫f_n(x)dx

II. Метод замены переменной

∫f(x)dx=|x=φ(t), dx=φ’(t)dt|=∫f(φ(t))φ’(t)dt

Группы интегралов берущихся с помощью одной и той же подстановки.

I.

II.

III.

IV.

{замена }

V.

30.

Интегралы от квадратного трехчлена

1.

;

2.

3.

+ln (сумма 2х интегралов)

4.

5.

Интегрирование по частям. u=u(x) и v=v(x)-дифф-емые ф-ци), du*v=u*dv+v*du→u*dv=duv-v*du→ - ф-ла интегрирования по частям.

Тригонометрические подстановки:

1) ,

2)

3)

31.Интегрирование рациональных дробей, некоторых иррациональных функций

R(x)=P(x)/Q(x),P(x),Q(x)-многочлены степени m и n, если m<n-правильная рац.дробь, если m=>n-неправ.рац дробь

P(x)/Q(x)-неправ.рац.дробь→P(x)/Q(x)=F(x)+ P1(x) /Q(x)

Среди правильных рациональных дробей разделяют 4 вида простых или простейших дробей

1) 2)

3) 4)

Теорема.Каждая правильная рациональная дробь может быть представлена в виде суммы конечного числа простых дробей

Разложение правильной дроби на простые связано с разложением знаменателя на множители.

(m-степ, n- степ ,m<n)

Установлено, что каждому множителю в разложении знаменателя соответствует сумма k простых дробей вида

, а каждому множителю соответствует сумма s простых дробей вида:

Т.о. зная разложение знаменателя на множители, мы знаем знаменатели тех простых дробей, на сумму которых разлагается данная рациональная дробь; числители этих простых дробей зависят от неопределенных коэффициентов.

1) правильная или неправильная

2) неправильная выделяем целую часть

3) разлагаем правильную на сумму простых дробей

4) берем инт-л от каждого слагаемого

Т.о. интегралы от любой рациональной функции берутся

Интегралы от некоторых иррациональных выражений.

R ( ) – рациональное ф-ция от

I.

II.

32.

Интегрирование некоторых тригонометрических ф-ций

1.

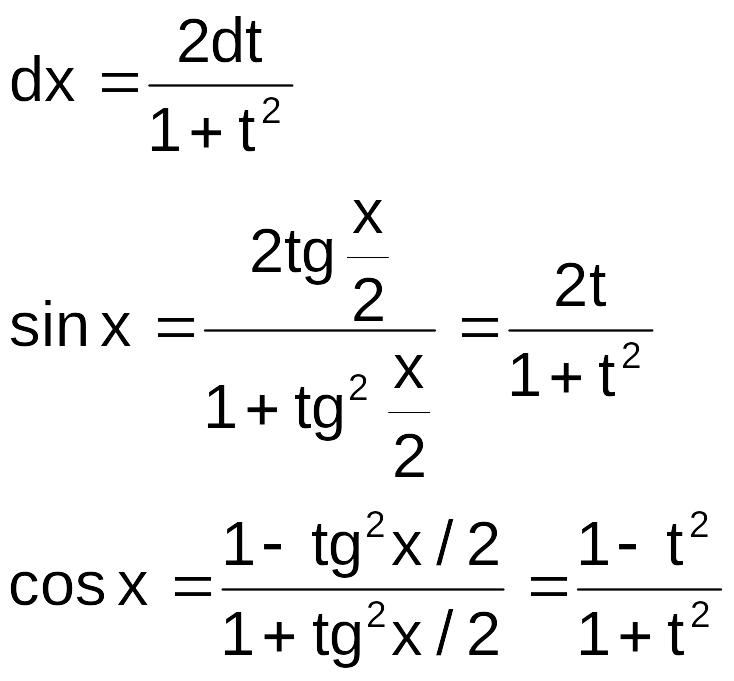
2.

3. (m и n – четные)

Формулы понижения степени:

Тригонометрические подстановки:

1) ,

2)

3)

33. Определенный интеграл и его свойства

Пусть функция f(x) задана на отрезке [а,b] выполним следующие действия:

1)Разбить [а,b] на части

d=max

-разбиение [а,b], d-диаметр разбиения

2) рассмотрим произвольную точку и назовем ее промежуточная, а также найдем значения f(x) в этой точке

3)составим интегральную сумму Римана

Если существует предел при d стремящимся 0 от ( lim(d→0)In) то он называется определенным интегралом по Риману от f(x) по отрезку[а,b]

И обозначается

Замечания:

Предел интегрирования суммы (определенный интеграл) не зависит от способа разбиения [а,b] на части и выбора промежуточных точек

Достаточное условие интегрируемости

Т. Если f(x) непрерывна на [а,b]то она интегрируема на этом отрезке

Геометрический смысл

1. f(x)≥0 [а,b], то

2. f(x) – знакопеременна на [а,b]

По определению полагаем

1) 2)

Свойства определенного интеграла:

1)

2)

3)

4) Если точка С разбивает [а,b] на [а,с] и [с,b], то интеграл

5)