
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №1.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №2.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №3.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №4.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №5.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №6.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №7.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №8.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №9.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №10.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №11.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №12.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №13.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №14.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №15.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №16.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №17.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №18.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №19.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №20.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №21.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №22.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №23.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №24.
- •Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №25.
Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №13.
1. Вычислить определенные интегралы:
1)
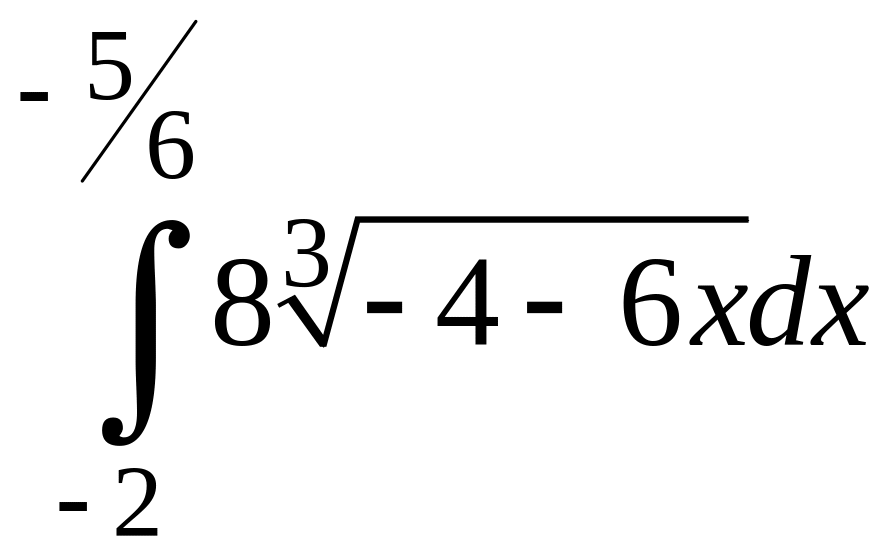 ;
2)
;
2)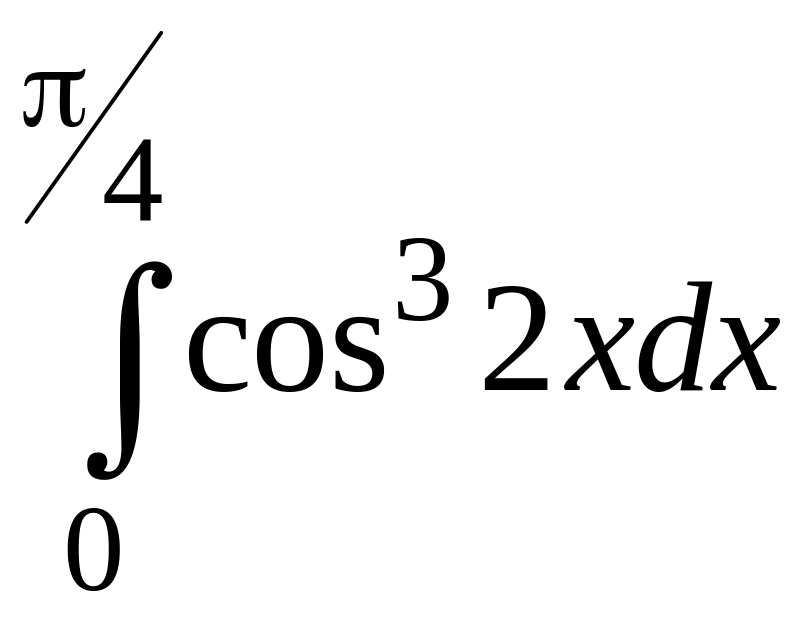 ;
3)
;
3)
 ;
4)
;
4)
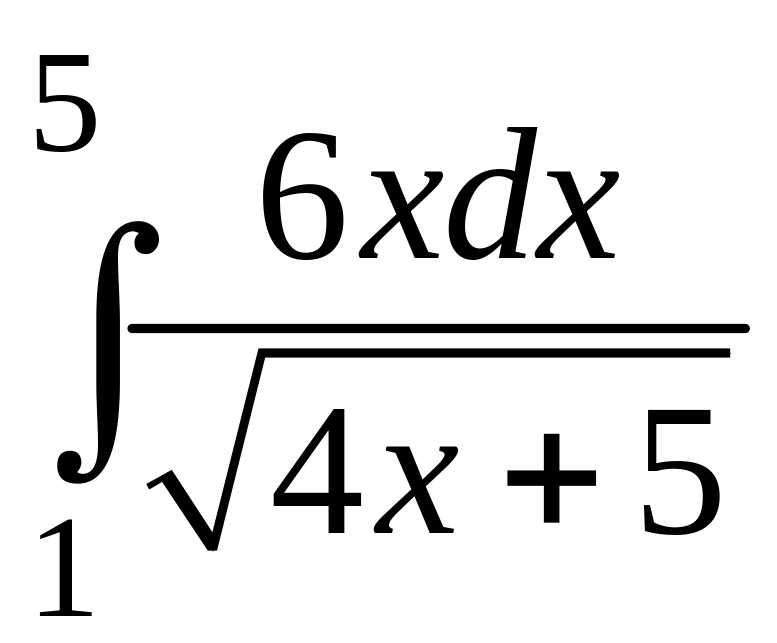 ;
5)
;
5)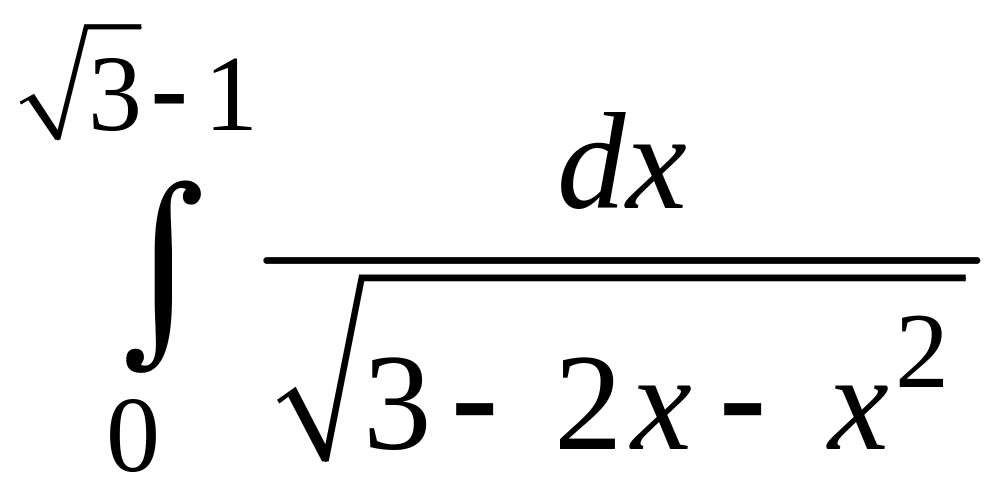 .
.
2. Вычислить площадь фигуры, ограниченной линиями:
![]()
3. Вычислить длину дуги кривой, заданной уравнением
![]() .
.
4. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
![]() вокруг оси OY.
вокруг оси OY.
5. Вычислить несобственные интегралы или установить их расходимость:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить двойной интеграл по области D, ограниченной линиями:
 .
.
7. Переходя к полярным координатам вычислить интеграл по области D, ограниченной
заданными линиями:
 .
.
8. С помощью двойного интеграла вычислить объём тела, ограниченного поверхностями:
гиперболоид , сфера .
9. Вычислить
,
если
 .
.
10. Вычислить
тройной интеграл
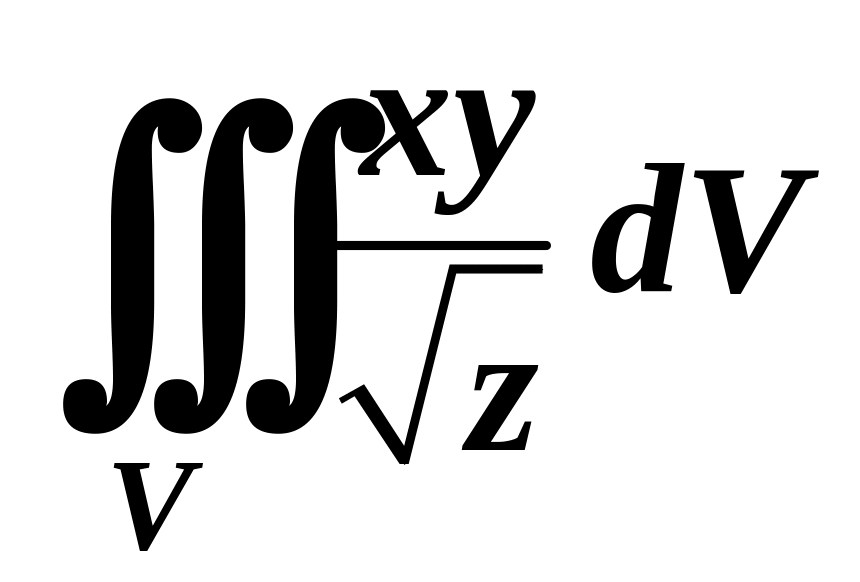 ,
перейдя к цилиндрическим координатам:
,
перейдя к цилиндрическим координатам:
![]() .
.
11. Найти координату xc центра масс тела, ограниченного указанными поверхностями:
![]() .
.
12. Вычислить криволинейный интеграл 1-го рода по ломаной ABC:
![]() .
.
13. Вычислить
поверхностный интеграл I-го
рода
![]() по поверхности
по поверхности
![]() .
.
Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №14.
1. Вычислить определенные интегралы:
1)
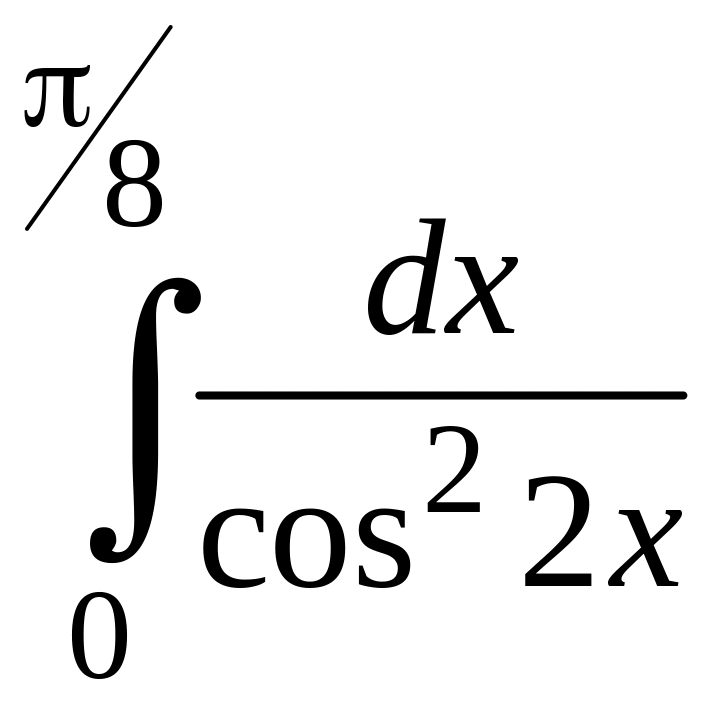 ;
2)
;
2) ;
3)
;
3)
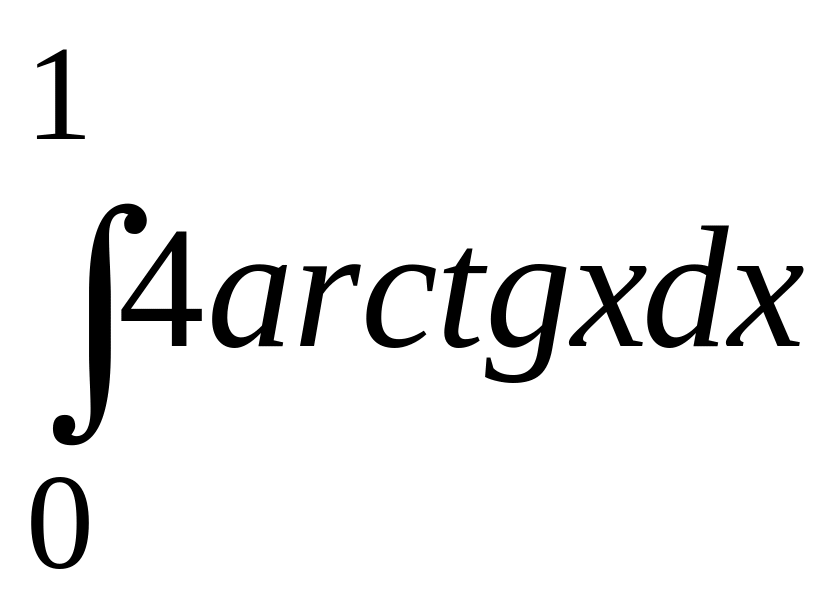 ;
4)
;
4)
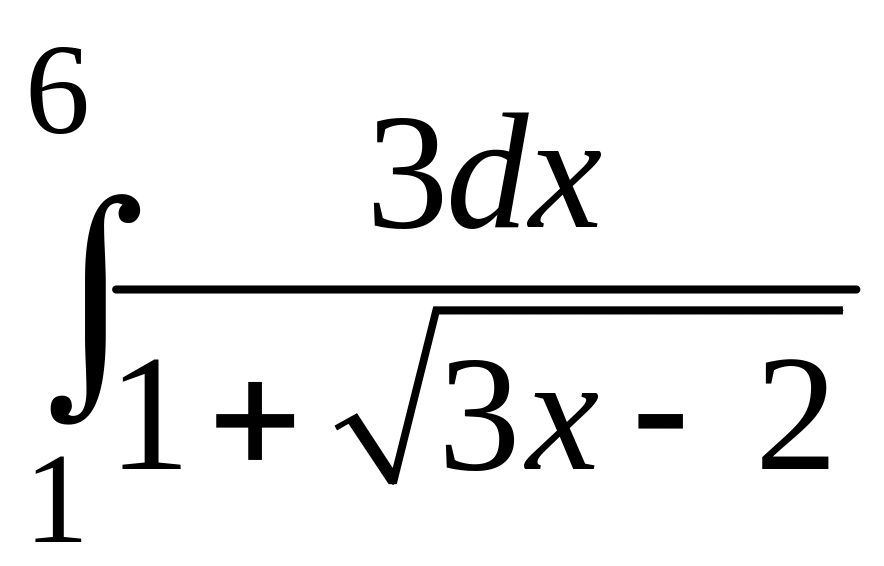 ;
5)
;
5) .
.
2. Вычислить площадь фигуры, ограниченной линиями:
![]()
3. Вычислить длину дуги кривой, заданной параметрически:
 .
.
4. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
![]() вокруг оси OY.
вокруг оси OY.
5. Вычислить несобственные интегралы или установить их расходимость:
1)
![]() ;
2)
;
2)
![]() .
.
6. Вычислить двойной интеграл по области D, ограниченной линиями:
 .
.
7. Переходя к полярным координатам вычислить интеграл по области D, ограниченной
заданными линиями:
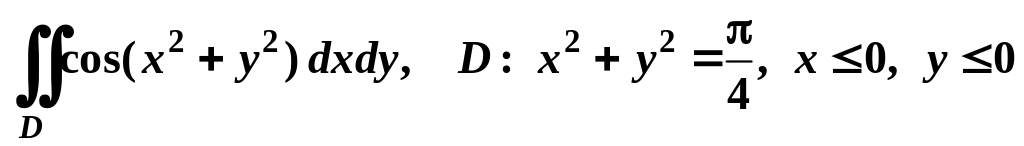 .
.
8. С помощью двойного интеграла вычислить объём тела, ограниченного поверхностями:
конус
![]() ,
параболоид
,
параболоид
![]() ..
..
9. Вычислить
,
если
 .
.
10.Вычислить тройной интеграл , перейдя к цилиндрическим координатам:
![]() .
.
11. Найти координату xc центра масс тела, ограниченного указанными поверхностями:
![]() .
.
12. Вычислить криволинейный интеграл 1-го рода по ломаной ABC:
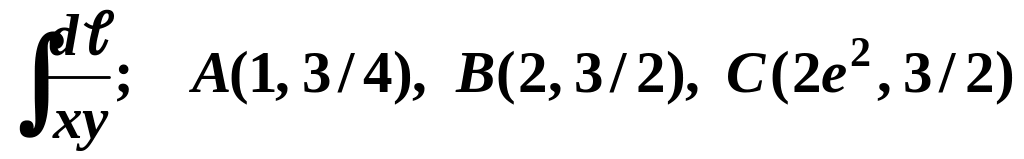 .
.
13. Вычислить
поверхностный интеграл I-го
рода
![]() по поверхности
по поверхности
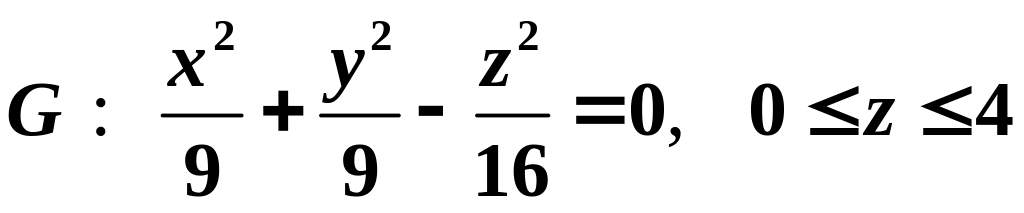 .
.
Типовой расчет по теме «Интегралы: определенные, несобственные, определенные по фигурам» Вариант №15.
1. Вычислить определенные интегралы:
1)
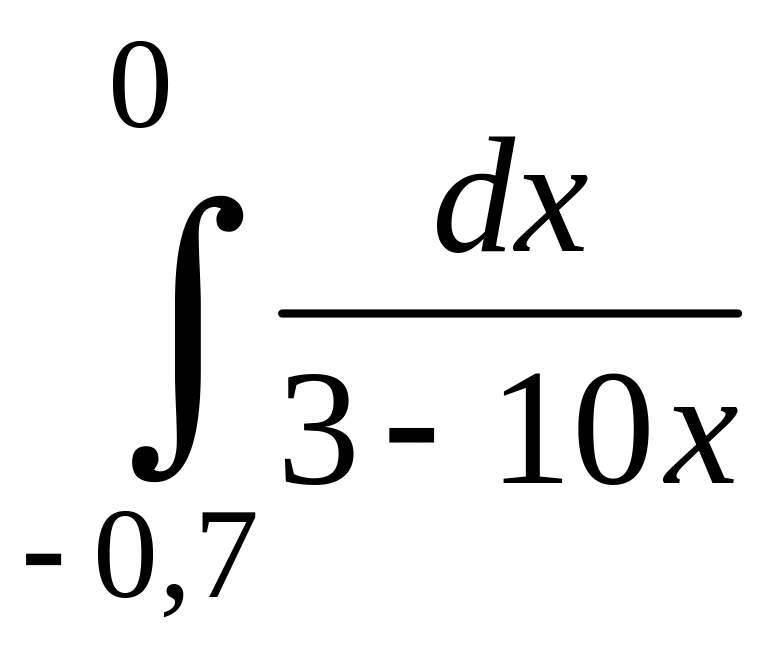 ;
2)
;
2) ;
3)
;
3)
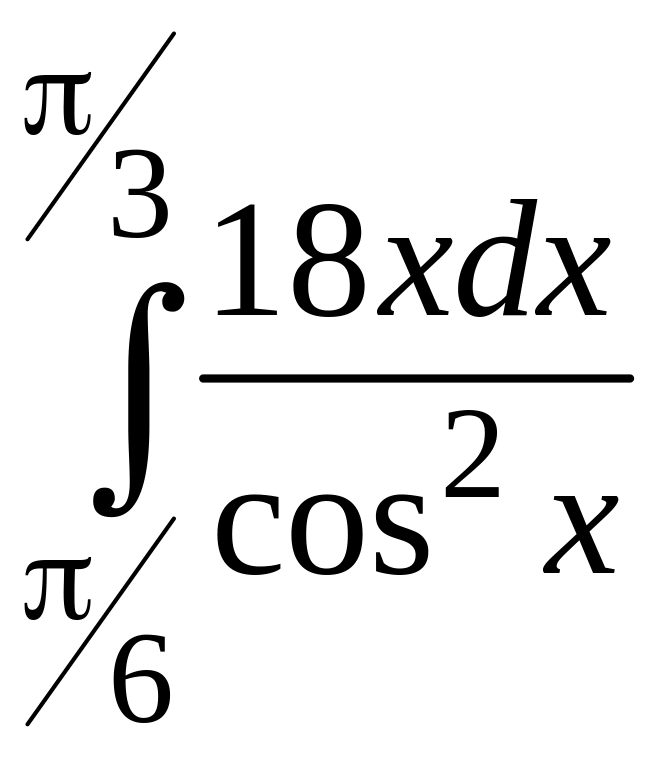 ;
4)
;
4)
 ;
5)
;
5)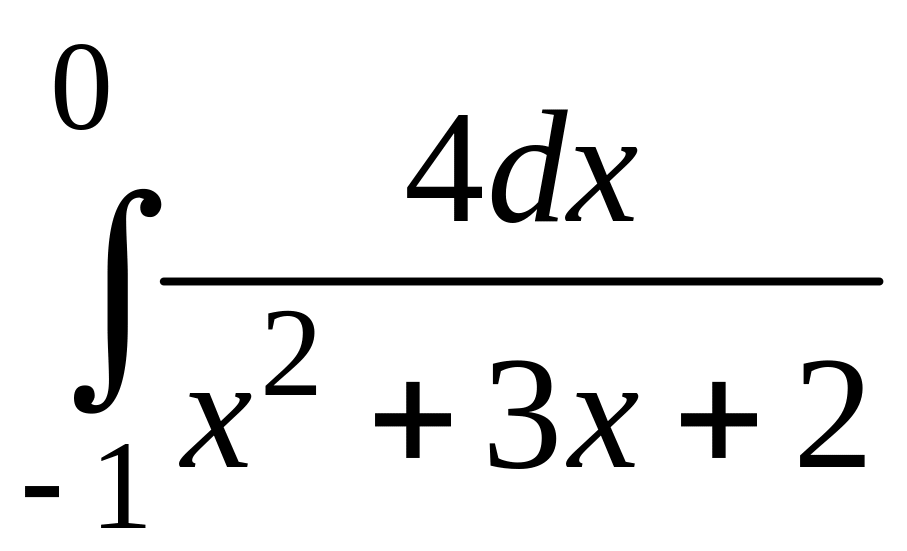 .
.
2. Вычислить площадь фигуры, ограниченной линиями:
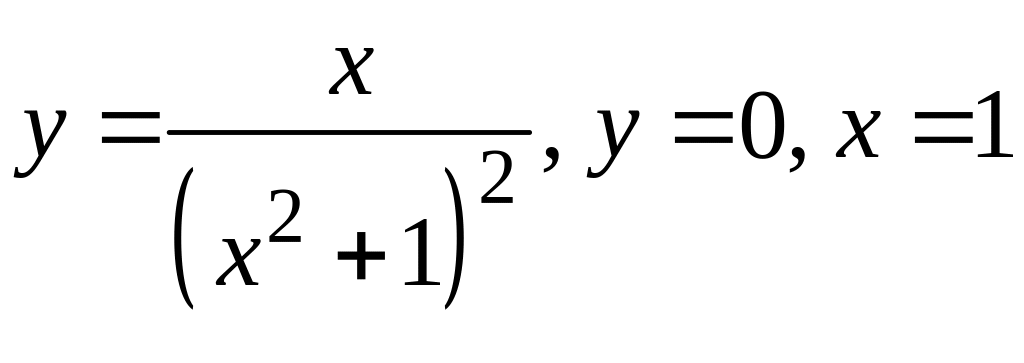
3. Вычислить длину дуги кривой, заданной уравнением
![]() .
.
4. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
![]() вокруг оси OY.
вокруг оси OY.
5. Вычислить несобственные интегралы или установить их расходимость:
1)
![]() ;
2)
;
2)
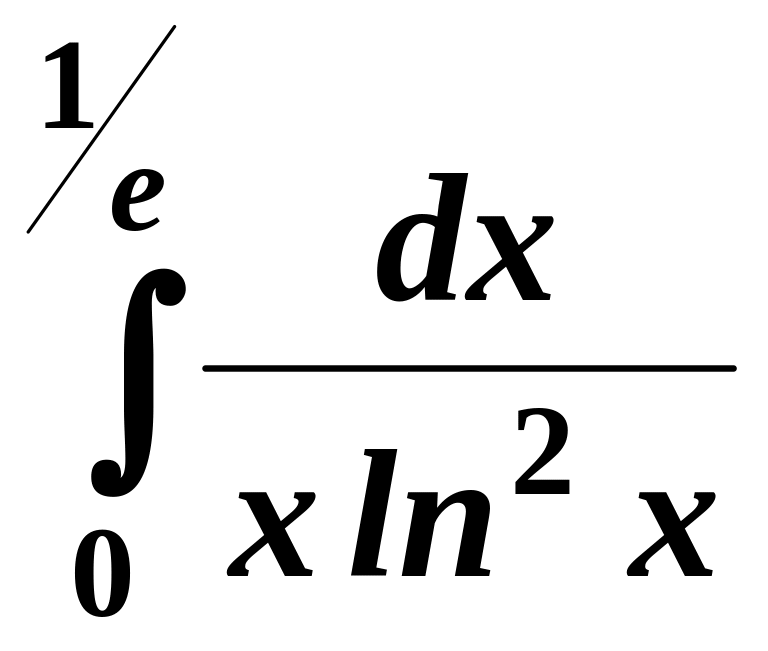 .
.
6. Вычислить двойной интеграл по области D, ограниченной линиями:
 .
.
7. Переходя к полярным координатам вычислить интеграл по области D, ограниченной
заданными линиями:
 .
.
8. Найти
площадь части поверхности
– сфера
![]() ,
вырезанной поверхностью
,
вырезанной поверхностью
– плоскость
![]() .
.
9. Вычислить
,
если
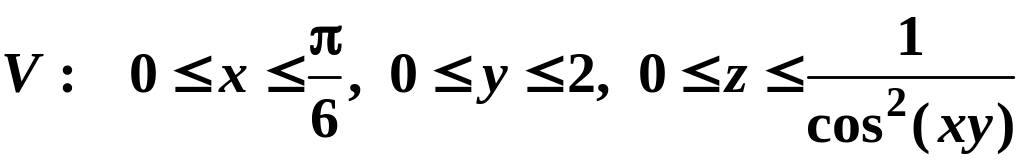 .
.
10. Вычислить
тройной интеграл
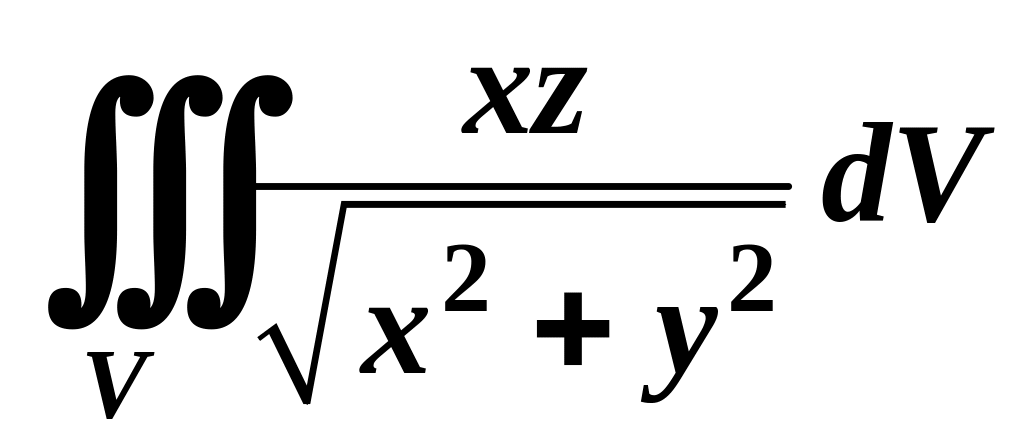 ,
перейдя к цилиндрическим
,
перейдя к цилиндрическим
координатам:
![]() .
.
11. Найти координату xc центра масс тела, ограниченного указанными поверхностями:
![]() .
.
12. Вычислить криволинейный интеграл 1-го рода по ломаной ABC:
![]() .
.
13. Вычислить
поверхностный интеграл I-го
рода
 по поверхности G
:
по поверхности G
:
![]() ,
вырезанная цилиндром
.
,
вырезанная цилиндром
.
