Раздел №2 Синтез системы автоматического регулирования.

1. Последовательная коррекция

При последовательной коррекции корректирующее звено включают в прямую цепь регулирования. Схема последовательной коррекции имеет вид:

При выборе последовательного корректирующего звена необходимо помнить, что дифференцирующие звенья увеличивают запас устойчивости системы и увеличивают ее быстродействие, интегрирующие – улучшают статику системы, но уменьшают запас устойчивости системы, безинерционные – уменьшают статическую ошибку системы (и, если К>1 и уменьшают при этом запас устойчивости системы).

В данном случае, мне необходимо уменьшить статическую ошибку. При этом величина максимального перерегулирования не должна превысить 25%, колебательность должна быть больше 75%, а время регулирования не должно превышать 60с. Из этих соображений я выбираю безинерционное звено, тогда W_исх. (р) и W_посл. (р) будут иметь вид:

Заменим W_исх. (р) и W_посл. (р) на эквивалентную функцию W_ск. (р)

Рассмотрим влияние этого звена на статику системы:

;

_{То есть введение безинерционного звена в прямую цепь регулирования уменьшает статическую ошибку до 0%.}

_{Влияние безинерционного звена на динамику рассмотрим с помощью АФЧХ скорректированной системы:}

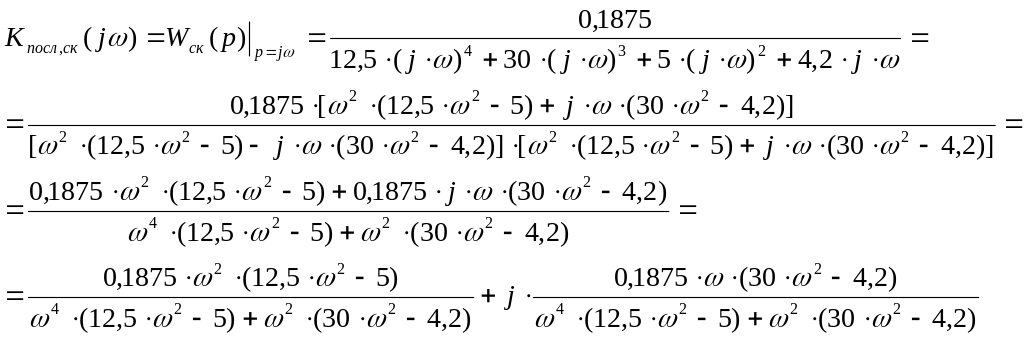
Таблица для построения годографа Найквиста.

Re	0	-0,06	-0,1	-0,25	-0,32	-0,32	0,002	-0,19	-0,41	0
Im	∞	-0,5	-0,27	-0,25	-0,21	0,15	0,016	0,19	0	0.04

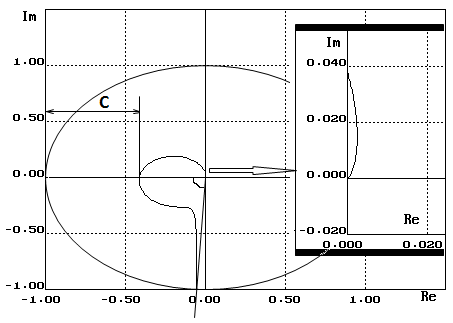
Как видно из годографа Найквиста система имеет запас устойчивости по модулю равный 0.69 и запас устойчивости по фазе равный 86^о.

Теперь по передаточной функции замкнутой системы построим кривую переходного процесса (на ЭВМ)

Передаточная функция замкнутой системы:

Построим для данной передаточной функции кривую переходного процесса по точкам, полученным из расчета на ЭВМ.

Таблица экспериментальных данных.

h(t)	0,00	0,55	0,55	0,8	0,8	0,91	0,91	0,95	0,98	1,01	1,00
t	1,5	14,7	20,4	30	40	46	55,5	68,4	76,88	90	95

Определение основных показателей качества по кривой переходного процесса.

1) Максимальное динамическое отклонение.

2) Время Регулирования

3) Величина максимального перерегулирования.

4) Колебательность процесса.

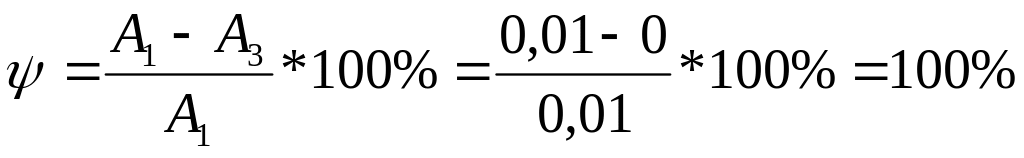
Вывод.

Применяя последовательную коррекцию к данной системе автоматического регулирования, и взяв в качестве корректирующего безинерционное звено, равное , удалось уменьшить статическую ошибку до 0 (улучшить статику), увеличить запас устойчивости по фазе до 86^о (улудшилась динамика). Теперь система отвечает требуемым показателям качества, т.к. величина максимального перерегулирования составляет 1%, колебательность процесса равна 100% и время максимального перерегулирования не превышает 60с. Данная система является в статике работоспособной и отвечает основным критериям в динамике.