Частотный критерий Михайлова.
Частотные критерии устойчивости позволяют судить об устойчивости систем автоматического управления по виду их частотных характеристик. САР устойчива, если при изменении частоты от 0 до ∞ годограф вектора ее характеристического уравнения (годограф Михайлова) проходит последовательно против часовой стрелки n квадрантов, не пропуская ни одного.
Передаточная функция замкнутой системы:
Характеристическое уравнение замкнутой системы:
Коэффициенты характеристического уравнения:
;
;
;
Заменив в характеристическом уравнении оператор р на оператор jω, получим вектор Нзам(jω).
Найдем
частоту
при которой годограф Михайлова пересечет
мнимую полуось.
Найдем
частоту
при которой годограф Михайлова пересечет
действительную полуось.
Таблица для построения годографа Михайлова.
|
0,00 |
0,30 |
’ = 0,68 |
1,00 |
’’ = 2.14 |
3,00 |
|
Re |
1,65 |
1,34 |
0,000 |
-1,83 |
-14,29 |
-29,67 |
-∞ |
Im |
0,000 |
1,17 |
2,43 |
3,11 |
0,000 |
-11,55 |
-∞ |
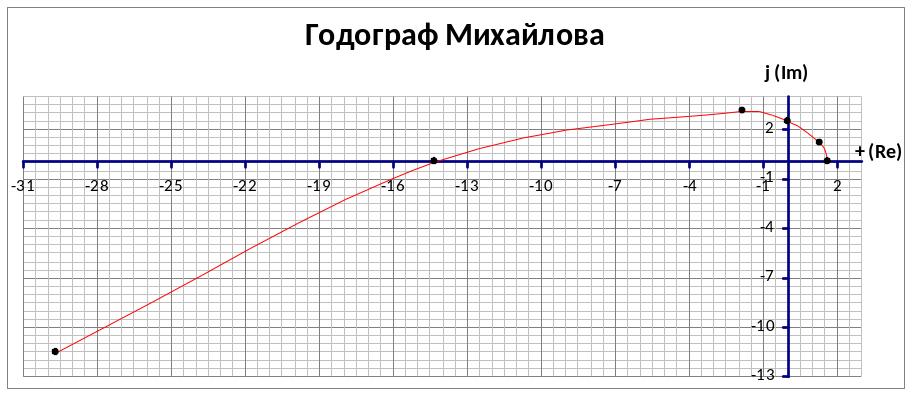
Годограф Михайлова проходит через три квадранта, не пропуская ни одного, следовательно, система устойчива по Михайлову.
Ширина годографа Михайлова:
Re(0) – Re(** )= 14,290 – (-1,650) = 15,94
Частотный критерий Найквиста.
Этот критерий позволяет судить об устойчивости замкнутых САР по амплитудно-фазовой характеристике разомкнутой САР. Замкнутая САР устойчива, если:
устойчива разомкнутая САР и её АФЧХ не охватывает точку с координатами (-1, j0);
не устойчива разомкнутая САР и её АФЧХ охватывает точку с координатами (-1, j0).
Передаточная функция разомкнутой системы:
Амплитудо-фазо-частотная характеристика системы:
;
Найдем частоту * при которой годограф Найквиста пересечет мнимую полуось.
Таблица для построения годографа Найквиста.
|
0,00 |
0,05 |
0,14 |
0,2 |
0,28 |
0,33 |
’ = 0,37 |
0,42 |
0,5 |
0,5 |
0,6 |
0,7 |
1 |
∞ |
Re |
0,446 |
0,453 |
0,5 |
0,57 |
0,74 |
0,76 |
0 |
-0,8 |
-0,62 |
-0,62 |
-0,28 |
-0,18 |
-0,07 |
0 |
Im |
0 |
-0,03 |
-0,09 |
-0,17 |
-0,45 |
-0,97 |
-1,52 |
-0,86 |
-0,18 |
-0,18 |
-0,01 |
0,01 |
0,02 |
0 |
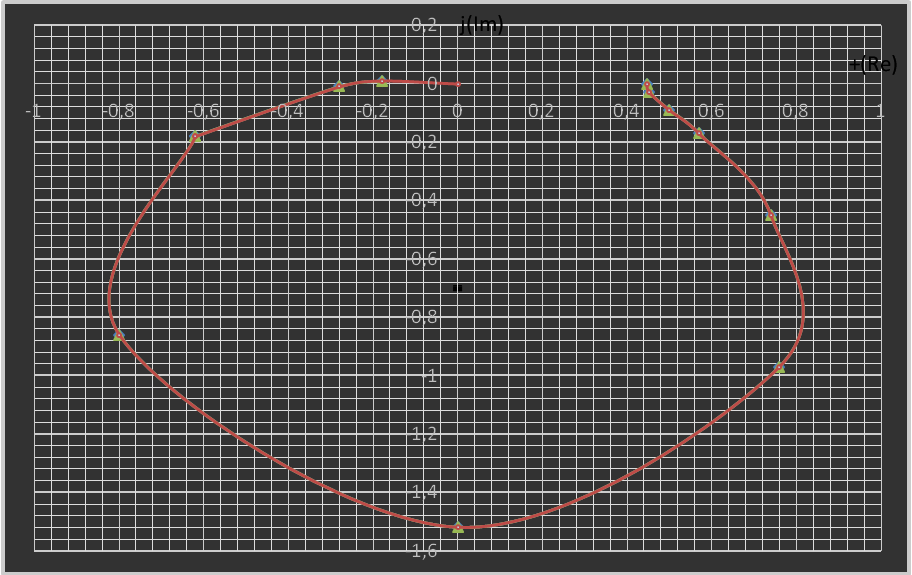
Замкнутая система устойчива (по Найквисту), т. к. устойчивая разомкнутая САР и её АФЧХ не охватывает точку с координатами (-1, j0).
Годограф Найквиста полученный на компьютере
