36. Цап, ацп, Арифметическое устройство

ЦАП и АЦП применяются в измерительной технике (цифровые осциллографы, вольтметры, генераторы сигналов и т.д.), в бытовой аппаратуре (телевизоры, музыкальные центры, автомобильная электроника и т.д.), в компьютерной технике (ввод и вывод звука в компьютерах, видеомониторы, принтеры и т.д.), в медицинской технике, в радиолокационных устройствах, в телефонии и во многих других областях. Применение ЦАП и АЦП постоянно расширяется по мере перехода от аналоговых к цифровым устройствам.

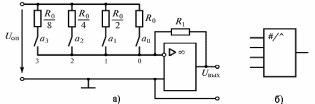
При использовании логических и цифровых устройств в системах автоматизированного управления возникает проблема связи их с различными электронными преобразователями входных сигналов и исполнительными механизмами, у которых в большинстве случаев информация представлена в аналоговой форме в виде различных уровней напряжения и тока. В этом случае для преобразования цифрового сигнала в аналоговый используют так называемый цифро-аналоговый преобразователь (ЦАП), а для обратного преобразования – аналого-цифровой преобразователь (АЦП). ЦАП и АЦП выполняют в виде больших интегральных схем. Конструктивно ЦАП состоит из операционного усилителя (рис. 16.4 а), на вход которого с помощью электронных ключей (например, ключи на МОП-транзисторах), управляемых двоичным кодом, подключается матрица резисторов.

Рис. 16.4

Коэффициент передачи определяется по отношению  . По входам 0, 1, 2, 3 коэффициенты передачи будут соответственно

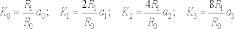  , (16.1)

где 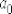  – 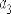  – числа, принимающие значения 0 или 1 в зависимости от положения соответствующего ключа. Выходное напряжение ЦАП определяется по формуле

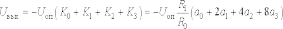.  (16.2)

Таким образом, двоичный код на входе ЦАП преобразуется на выходе в уровень напряжения  .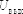

Недостатками этой схемы ЦАП являются необходимость жестких требований к точности и стабильности сопротивлений матрицы, особенно старших разрядов, а также к качеству опорного напряжения 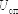  источника питания при различных нагрузках. Условное обозначение ЦАП показано на рис. 16.4 б.

Аналого-цифровой преобразователь состоит из цифрового автомата (ЦА) (рис. 16.5), который по сигналу, поступающему на его вход, вырабатывает последовательность соответствующих чисел в двоичном коде. Этот код подается на вход ЦАП, где формируется выходное напряжение 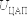 , определяемое входными числами. Напряжение   подается на вход компаратора, где сравнивается с входным напряжением 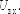  Если напряжения 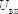  и   равны, то компаратор выдает сигнал, останавливающий работу цифрового автомата, и на его выходе в запоминающих буферных устройствах фиксируется соответствующий двоичный код.

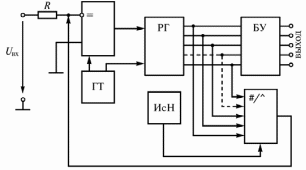
Цифровой автомат представляет собой двоичный регистр (РГ), основное назначение которого – запись и хранение информации в двоичном коде. Основными элементами регистра являются триггеры. Их число определяется числом двоичных разрядов, на которое рассчитан регистр. Регистр суммирует импульсы от тактового генератора (ТГ). В выходном буферном устройстве (БУ) хранятся числа в двоичном коде, поступающие от регистра. Вся схема питается от источника стабилизированного напряжения (ИсН).

Рис. 16.5

Импульсы, поступающие от тактового генератора на вход регистра, переводят его разряды в код 1, начиная со старшего разряда. Если старший разряд имеет код 1, ЦАП выдает на выходе соответствующее напряжение, которое сравнивается в компараторе с входным напряжением. Если   и   больше  , то старший регистр получает код 0, в противном случае остается 1. Далее код 1 появляется в следующем разряде и цикл повторяется до младшего разряда регистра. После этого АЦП готов к выдаче кода из регистра.

(тут другая статья про АЦП просто здесь схемы похожи на те, что он нам рисовал.)

АЦП последовательного приближения АЦП последовательного приближения реализует алгоритм «взвешивания», восходящий еще к Фибоначчи. В своей книге «Liber Abaci» (1202 г.) Фибоначчи рассмотрел «задачу о выборе наилучшей системы гирь», то есть о нахождении такого ряда весов гирь, который бы требовал для нахождения веса предмета минимального количества взвешиваний на рычажных весах. Решением этой задачи является «двоичный» набор гирь. Подробнее о задаче Фибоначчи можно прочитать, например, здесь:http://www.goldenmuseum.com/2015AMT_rus.html. Аналого-цифровой преобразователь последовательного приближения (SAR, Successive Approximation Register) измеряет величину входного сигнала, осуществляя ряд последовательных «взвешиваний», то есть сравнений величины входного напряжения с рядом величин, генерируемых следующим образом: 1. на первом шаге на выходе встроенного цифро-аналогового преобразователя устанавливается величина, равная 1/2Uref (здесь и далее мы предполагаем, что сигнал находится в интервале (0 – Uref). 2. если сигнал больше этой величины, то он сравнивается с напряжением, лежащим посередине оставшегося интервала, т.е., в данном случае, 3/4Uref. Если сигнал меньше установленного уровня, то следующее сравнение будет производиться с меньшей половиной оставшегося интервала (т.е. с уровнем 1/4Uref). 3. Шаг 2 повторяется N раз. Таким образом, N сравнений («взвешиваний») порождает N бит результата. 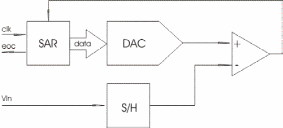Рис. 2. Структурная схема АЦП последовательного приближения. Таким образом, АЦП последовательного приближения состоит из следующих узлов: 1. Компаратор. Он сравнивает входную величину и текущее значение «весового» напряжения (на рис. 2. обозначен треугольником). 2. Цифро-аналоговый преобразователь (Digital to Analog Converter, DAC). Он генерирует «весовое» значение напряжения на основе поступающего на вход цифрового кода. 3. Регистр последовательного приближения (Successive Approximation Register, SAR). Он осуществляет алгоритм последовательного приближения, генерируя текущее значение кода, подающегося на вход ЦАП. По его названию названа вся данная архитектура АЦП. 4. Схема выборки-хранения (Sample/Hold, S/H). Для работы данного АЦП принципиально важно, чтобы входное напряжение сохраняло неизменную величину в течение всего цикла преобразования. Однако «реальные» сигналы имеют свойство изменяться во времени. Схема выборки-хранения «запоминает» текущее значение аналогового сигнала, и сохраняет его неизменным на протяжении всего цикла работы устройства. Достоинством устройства является относительно высокая скорость преобразования: время преобразования N-битного АЦП составляет N тактов. Точность преобразования ограничена точностью внутреннего ЦАП и может составлять 16-18 бит (сейчас стали появляться и 24-битные SAR ADC, например, AD7766 и AD7767). Дельта-сигма АЦП И, наконец, самый интересный тип АЦП – сигма-дельта АЦП, иногда называемый в литературе АЦП с балансировкой заряда. Структурная схема сигма-дельта АЦП приведена на рис. 3. 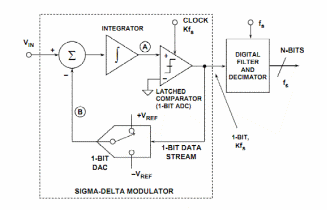Рис.3. Структурная схема сигма-дельта АЦП. Принцип действия данного АЦП несколько более сложен, чем у других типов АЦП. Его суть в том, что входное напряжение сравнивается со значением напряжения, накопленным интегратором. На вход интегратора подаются импульсы положительной или отрицательной полярности, в зависимости от результата сравнения. Таким образом, данный АЦП представляет собой простую следящую систему: напряжение на выходе интегратора «отслеживает» входное напряжение (рис. 4). Результатом работы данной схемы является поток нулей и единиц на выходе компаратора, который затем пропускается через цифровой ФНЧ, в результате получается N-битный результат. ФНЧ на рис. 3. Объединен с «дециматором», устройством, снижающим частоту следования отсчетов путем их «прореживания». 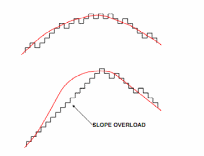Рис. 4. Сигма-дельта АЦП как следящая система Ради строгости изложения, нужно сказать, что на рис. 3 изображена структурная схема сигма-дельта АЦП первого порядка. 

Основными характеристиками ЦАП и АЦП являются быстродействие, погрешность и динамический диапазон изменения входного напряжения для АЦП и выходного для ЦАП.

ЦАП и АЦП являются основным связующим звеном между ЭВМ и различными периферийными устройствами автоматизированных систем управления технологическими процессами.

Арифметическое устройство

Арифметическая часть ЦП может варьироваться от простого сумматора до сложного блока, который выполняет многие арифметические и логические функции. Если арифметическое устройство не может выполнить операцию аппаратным способом, то для получения желаемого результата необходимо использовать последовательность команд. Все современные ЭВМ имеют двоичные сумматоры, принимающие два двоичных входных сигнала и получающие двоичную сумму и признак переноса в старшем значащем разряде суммы. Так как большинство ЭВМ оперирует с дополнительным кодом, то вычитание может быть выполнено путем подачи на один из входов сумматора числа в дополнительном коде. Умножение и деление может быть выполнено с помощью повторяющихся операций сложения и вычитания соответственно. Дополнительные схемы могут сформировать другие признаки результата, такие как, например, нулевое значение. Широко применяются в микроэлектронной технике однокристальные арифметическо-логические устройства (АЛУ). Эти устройства состоят из двоичного сумматора и вспомогательных логических схем. Типичное АЛУ показано на рис. 2.15. Оно имеет два входа данных, функциональные входы, вход признака переноса для выполнения операций умножения и деления, выходы данных и состояний, которые представляют собой различные признаки, описанные в предыдущем параграфе. Функциональные входы определяют, какую операцию решает АЛУ. Типичные операции: сложение, вычитание, логическое И, логическое (включающее) ИЛИ, логическое ИСКЛЮЧАЮЩЕЕ ИЛИ, логическое НЕ (дополнение), инкрементирование (увеличение на 1), декрементирование (уменьшение на 1), сдвиг влево (сложение входного сигнала с самим собой), обнуление (результат равен 0). Функциональные входы также определяют режим работы шины. Например, число, представленное в шине А, может быть увеличено на 1 путем маскирования шины В (число, поступающее в АЛУ по шине В, равно 0), установки в 1 входа признака переноса и сложения. Таким образом, OUTPUT = А + В + CARRY = А+ 0+1 = А + 1 Другие операции позволяют выполнять сравнение входной или выходной величины с целью решения задач типа А 4- В или А • В. Таким образом, АЛУ может решать любую из разнообразных задач в течение одного цикла под управлением сигналов на функциональных входах.

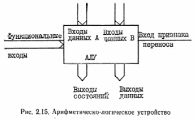При помощи специальных дополнительных схем могут также решаться другие арифметические задачи, такие как умножение и деление, нахождение синуса и косинуса, определение логарифмов или экспонент. Эти специальные схемы способны обеспечизать высокое быстродействие, но арифметические блоки, которые могут непосредственно решать специализированные задачи, стоят гораздо дороже, чем стандартные блоки АЛУ.