21

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Южно-Российский технический университет

(НПИ)

Факультет автоматики и управления

Кафедра автоматики и телемеханики

А.Г.Малашенко

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к лабораторным работам по дисциплине «ИНФОРМАТИКА»

Часть 2

для студентов направления «Электроника и наноэлектроника»

НОВОЧЕРКАССК 2014

УДК 519.6 (076.3)

А.Г.Малашенко

Методические указания к лабораторным работам

по дисциплине "Информатика".

для студентов направления «Электроника и наноэлектроника»

Часть 2.

В работе изложены цель, программа выполнения лабораторных работ, контрольные вопросы, содержание отчета, методические указания и сведения о литературе, необходимой для подготовки к работе.

Методические указания предназначены для студентов первого курса.

Объем стр., тираж экз.

Методические указания обсуждены и одобрены на заседании кафедры "Автоматика и телемеханика"

ФИТУ ЮРГТУ(НПИ),

протокол № от 2014 г

Южно-Российский государственный технический университет (НПИ), 2014

Введение

Для выполнения лабораторных работ требуется IBM-совместимый персональный компьютер с операционной системой MS Windows XP и выше и прикладное ПО: графический процессор и пакет MicroCap (EWB).

Подготовка к работе заключается в повторении лекционного материала по теме работы и дополнительного изучения по указанной рекомендованной литературе или по материалам электронных источников.

При выполнении лабораторной работы следует руководствоваться методическими указаниями к работе.

В отчете по каждой работе должны быть представлены:

1. наименование и программа работы;

2. содержание индивидуального задания;

3. результаты выполнения пунктов программы;

Для самоконтроля повторенного теоретического материала и приобретенных навыков можно использовать контрольные вопросы.

Лабораторная работа № 7 Этапы разработки по

Цель работы: Знакомство с процессом разработки ПО и приобретение навыков алгоритмизации.

Продолжительность работы – 6 часа

Подготовка к работе

Изучить по материалам лекций и учебной литературе следующие вопросы:

1. Этапы разработки ПО.

2. Схемы алгоритма, основные алгоритмические структуры: следование, развилка и цикл.

3. Этап алгоритмизации. Типовые вычислительные алгоритмы.

4. Этап отладки, тестирование программ.

Программа работы

1. Рассмотреть пример этапов разработки прикладной задачи.

2. Ознакомиться с элементами схем алгоритма в соответствии с требованиями ЕСКД.

3. Изобразить схемы трех базовых алгоритмических структур: следование, развилка и цикл.

4. Сделать постановку прикладной задачи по индивидуальному заданию для своего варианта

5. Разработать тест для проверки правильности алгоритма.

6. Разработать алгоритм и изобразить его схему.

7. Проверить правильность алгоритма с помощью разработанного в п.5 теста

Методические указания к работе

К п. 1. По заданию преподавателя перечислить этапы разработки программы и их содержание.

1. Постановка задачи. Программа должна находить определенный интеграл I от заданной функции F(x) на известных пределах от a до b:

2. Выбор метода решения. Определенный интеграл графически представляет собой площадь, ограниченную графиком подынтегральной функции, границами нижнего и верхнего пределов и осью абсцисс, поэтому взятие интеграла можно заменить нахождением величины этой площади.

Приближенно площадь можно найти различными численными методами. В нашем примере мы будем использовать метод левых прямоугольников. Суть его заключается в том, что

. Суть метода заключается в следующем.

Разделим отрезок [a; b] на n равных частей, т.е. на n элементарных отрезков. Длина каждого элементарного отрезка h = (a-b)/n. Точки деления будут: x₀=a; x₁=a+h; x₂=a+2*h, ... , x_n-1=a+(n-1)*h; x_n=b. Эти числа будем называть узлами. Вычислим значения функции f(x) в узлах, обозначим их y₀, y₁, y₂, ... , y_n. Cтало быть, y₀=f(a), y₁=f(x₁), y₂=f(x₂), ... , y_n=f(b). Числа y₀, y₁, y₂, ... , y_n являются ординатами точек графика функции, соответствующих абсциссам x₀, x₁, x₂, ... , x_n. Площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы n элементарных прямоугольников.

Формула левых прямоугольников: 

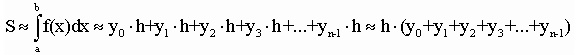
Графически метод можно представить рисунком 1.

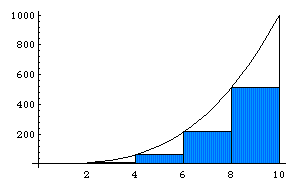
Рисунок 1 – приближенное вычисление интеграла.

К п.2. Рассмотреть правила изображения элементов схем алгоритма.

Правила изображения элементов и построения схем алгоритма определяются единой системой программной документации (ЕСПД), которая состоит из набора стандартов. Каждый пункт алгоритма отображается на схеме некоторой геометрической фигурой-блоком, причем различным по типу выполняемых действий блокам соответствуют различные геометрические фигуры, изображаемые по ГОСТу.

На рисунке 2 изображены графические изображения стандартных действий алгоритма:

процесс (а), решение (б) и слияние(в).

а б в

Рисунок 2

Основными алгоритмическими структурами являются:

• Следование

• Развилка

• Цикл

Структура «Следование»

Следованием называется конструкция, представляющая собой последовательное выполнение двух или более операций.

На рисунке 3 показана структура «следование», реализующая линейный алгоритм.

На схемах «Процесс» обозначает один или несколько операторов.

Пример. Пешеход шел по пересеченной местности. Он прошел t1 ч времени со скорость движения v1 км/ч по равнине, t2 ч со скоростью v2 км/ч в гору и t3 ч со скоростью v3 км/ч под гору. t1, t2 и t3 ч. Какой путь прошел пешеход? Схема алгоритма расчета пути показана на рисунке 4.

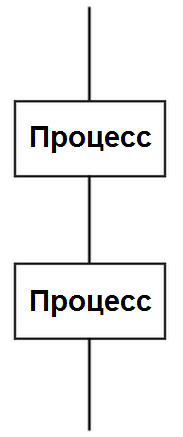
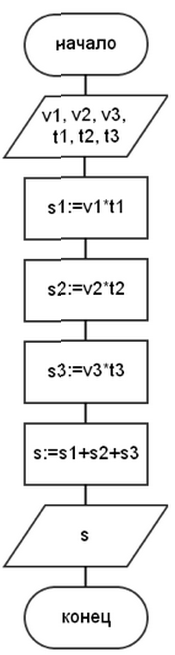
Рисунок 3 Рисунок 4

Структура «Развилка»

Действие должно быть выполнено в зависимости от значения логического выражения, выступающего в качестве условия. Различают неполную и полную развилку.

При неполной развилке (рисунок 5) если логическое выражение (ЛВ), представляющее собой некое условие, выполняется (ИСТИНА), тогда происходит переход по ветви ДА, иначе (ЛОЖЬ) – по ветви НЕТ.

При полной развилке (рисунок 6) при выполнении или невыполнении условия происходит какое-либо действие

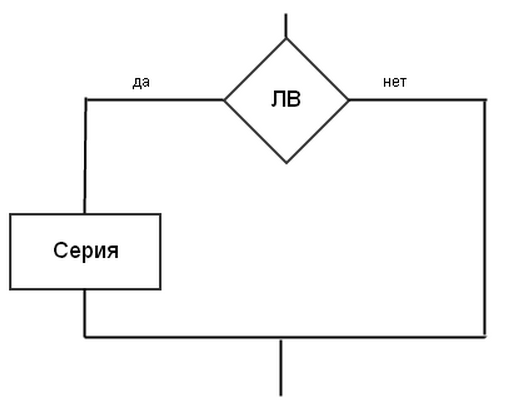
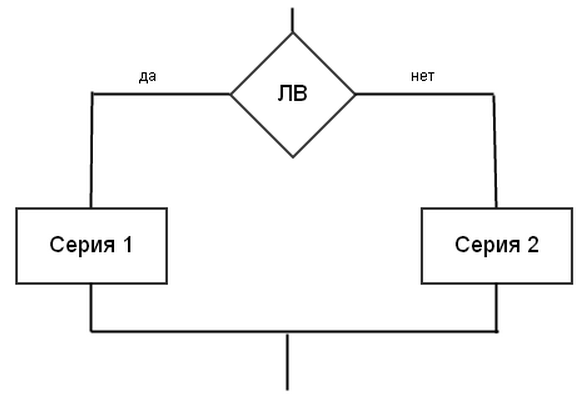
Рисунок 5 Рисунок 6

Структура «Цикл»

Конструкция, имеющая линии управления, ведущие к предыдущим операциям или развилкам, называется циклом.

На рисунках 7, 8 и 9 показаны разновидности структуры «цикл», реализующей циклический алгоритм – цикл с предусловием (ПОКА), цикл с постусловием (ДО), цикл с параметром соответственно.

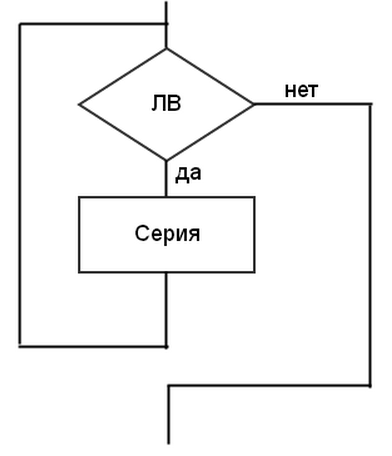
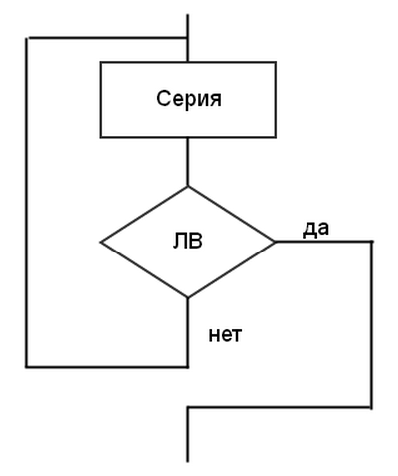
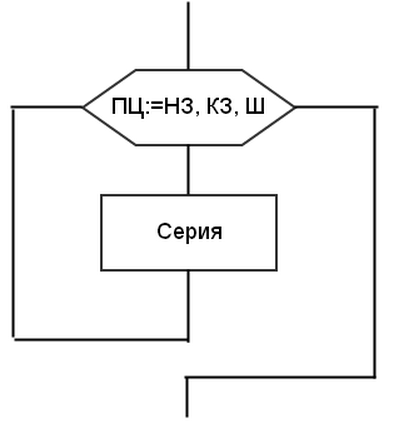
Рисунок 7 Рисунок 8 Рисунок 9

На рисунке 9: ПЦ — параметр цикла, НЗ — начальное значение параметра цикла, КЗ — конечное значение параметра цикла, Ш — шаг изменения параметра цикла.

К п. 3. Изобразить для конкретных заданий схемы с использованием трех базовых алгоритмических структур.

Примеры:

Следование. Ввести 3 исходных данных а,в,с , вычислить значение Y по известной формуле, вывести результат.

Развилка. Ввести 3 исходных данных а,в,с . Если a+b>c, то вычислить значение Y по формуле 1, в противном случае вычислить значение Y по формуле 2 и вывести результат.

Цикл. Вычислить и вывести таблицу значений функции F для значений аргумента от n до m c шагом 0,1 и построить график этой функции.

П.3 выполняется самостоятельно под контролем преподавателя.

К п. 4. По индивидуальному заданию сделать математическую постановку задачи, определить, что является исходными данными, какие данные представлены в компьютере, что является результатом.

Например, в задаче п.1 исходными данными являются значения пределов a и b и число отрезков на интервале n. В компьютере должно быть выражение подынтегральной функции F(x). Результатом будет значение интеграла I.

К п.5. Разработать тест, то-есть, подготовить такой набор данных, чтобы можно было сделать расчет вручную. Но при этом он должен обеспечивать проверку всех ветвей алгоритма. Для примера п.1 a=1, b=7, n=3. F= 2x+1;

Площади равны Si=(b-a)/n* F(Xi)

При x=1 S1=2*3, при x= 3 S2= 2*7. при x= 5 S3= 2*11

Интеграл равен сумме площадей I =44.

К п.6. Проанализировав ход решения тестовой задачи, разработать алгоритм и изобразить его схему. Схему можно изобразить вручную, либо используя изученный в первом семестре пакет MS Visio, либо MS Word.

Для задачи п.1 схема будет иметь вид, представленный на рисунке 10.

Пример для задачи п.1

а = 2, b = 10, n = 4, f= 2x+1.

Рисунок 10

К .7. Не используя вычисления п.5, произвести прокрутку алгоритма, т.е. выполнить действия для исходных данных теста по схеме алгоритма, как это будет выполнять компьютер. В ходе прокрутки необходимо выполнять действия и производить вычисление на каждом шаге и записывать их в отчет.

В случае несовпадения результатов теста и прокрутки ошибки в алгоритме можно найти путем сравнения по шагам вычисления результата теста и результата прокрутки алгоритма теста.

Варианты задания лабораторной работы №7

Для группы 1-1а

№ варианта	Содержание индивидуального задания
1	Нахождение определенного интеграла методом правых прямоугольников
2	Вычисление значения функции через сумму ряда
3	Определение количества элементов заданной величины в векторе
4	Решение нелинейного уравнения методом Ньютона
5	Нахождение произведения элементов четных строк матрицы
6	Перевод целого числа из десятичной системы в двоичную
7	Нахождение числа указанной буквы в слове
8	Нахождение скалярного произведения векторов С и D
9	Выдача сдачи в рублях из кассы с тремя купюрами
10	Нахождение суммы отрицательных элементов матрицы
11	Определение количества нечетных элементов в последовательности чисел
12	Нахождение максимального элемента вектора
13	Перевод числа из восьмеричной системы в десятичную
14	Нахождение среднего арифметического нечетных элементов вектора
15	Вставка в упорядоченный по возрастанию ряд чисел заданного числа
16	Нахождение суммы четных строк матрицы
17	Нахождение фамилий студентов, оценки которых выше среднего балла группы
18	Нахождение вектора С, элементы которого равны сумме элементов векторов А и В
19	Нахождение суммы нечетных столбцов матрицы
20	Нахождение произведения элементов нечетных столбцов матрицы
21	Нахождение максимального элемента в заданной строке матрицы
22	Нахождение среднего арифметического положительных элементов матрицы
23	Нахождение суммы первых N положительных элементов вектора
24	Удаление их последовательности цифр нулей.
25	Нахождение среднего арифметического нечетных элементов вектора

Для группы ФМФ 1-1

№ варианта	Содержание индивидуального задания
1	Вычисление интеграла методом трапеций
2	Решение нелинейного уравнения методом простой итерации
3	Нахождение суммы положительных элементов матрицы
4	Перевод целого числа из двоичной системы в десятичную
5	Нахождение определенного интеграла методом центральных прямоугольников
6	Нахождение произведения элементов нечетных строк матрицы
7	Нахождение максимального элемента вектора
8	Нахождение числа последовательности указанных буквы в слове
9	Вычисление значения функции через сумму ряда
10	Определение количества четных элементов в последовательности чисел
11	Нахождение произведения элементов четных столбцов матрицы
12	Перевод числа из восьмеричной системы в десятичную
13	Вставка в упорядоченный по убыванию ряд чисел заданного числа
14	Нахождение суммы первых N отрицательных элементов вектора
15	Нахождение скалярного произведения векторов А и В
16	Выдача сдачи монетами из кассы с 5 руб.,2 руб. и 1 руб.
17	Нахождение вектора С, элементы которого равны разности элементов векторов А и В
18	Нахождение суммы нечетных строк матрицы
19	Перевод числа из шестнадцатеричной системы в десятичную
20	Нахождение среднего арифметического ненулевых элементов матрицы
21	Нахождение суммы нечетных столбцов матрицы
22	Нахождение фамилий студентов, оценки которых ниже среднего балла группы
23	Удаление из строки текста пробелов
24	Нахождение минимального элемента в заданной строке матрицы
25	Преобразование фамилии, имени, отчества в инициалы.