Простейшая многоканальная система.

Обобщение методики построения моделирующих алгоритмов для случая простейших многоканальных систем не встречает принципиальных затруднений. В самом деле, пусть, например, речь идет о многоканальной системе массового обслуживания, содержащей n идентичных каналов. Заявки образуют ординар­ный поток однородных событий с заданным законом распреде­ления и принимаются к обслуживанию в порядке очереди (в по­рядке поступления в систему) Если поступившая заявка застает все каналы занятыми, то она ожидает освобождения канала, но не более чем , после чего получает отказ. Время обслужи­вания - случайная величина. Для обслуживания заявок при­влекаются свободные каналы в порядке очереди (прежде ис­пользуется тот канал, который освободился ранее других).

Легко видеть, что рассматриваемая многоканальная система по своему характеру близка к той одноканальной системе, ко­торую мы изучали в начале § 5.3. Поэтому при построении мо­делирующего алгоритма мы будем ориентироваться на алго­ритм (5.69).

Заменим в операторах Р3, P6, F7 алгоритма (5.69) величину на min , под которой будем понимать наименьшее время освобождения одного из каналов системы. Соответствующие операторы будем обозначать в дальнейшем Р3, P6, F7. Кроме того, введем дополнительно новый оператор А20 — выбор min наименьшего из . В операторах А10 и Р11 (теперь они будут обозначаться А10 и Р11) вместо необходимо иметь, где индекс k обозначает номер линии.

Наконец, можно записать операторную схему моделирую­щего алгоритма. Она аналогична схеме (5.69):

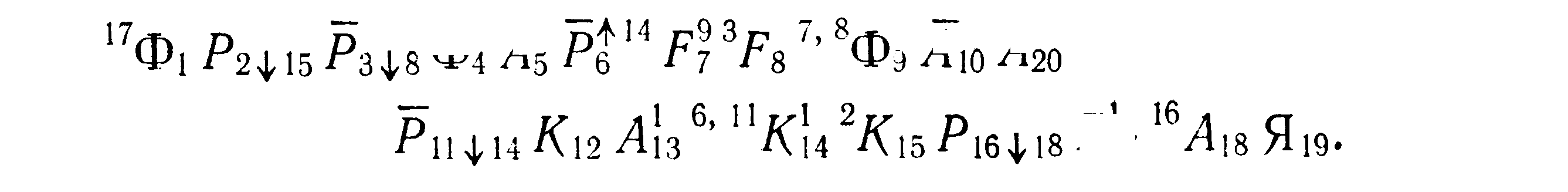
(5.75)

С точки зрения процесса работы алгоритм (5.75) также близок к (5.69). Поэтому на описании его мы останавливаться не будем.

Настоящим примером мы подтвердили сказанное выше о возможности обобщения методов моделирования на многока­нальные системы массового обслуживания. Необходимо отме­тить, что структура моделирующего алгоритма зависит от тех предположений, которые сделаны относительно дисциплины оче­реди заявок и порядка выбора каналов для обслуживания. Рас­смотренный выше пример относится к наиболее простым пред­положениям. Выбор заявки из очереди по наименьшему , как в случае. (5.72), в сочетании с другими правилами выбора каналов может привести к заведомо более сложному модели­рующему алгоритму.

Во многих случаях под алгоритм, обеспечивающий выбор ка­нала для обслуживания в соответствии с заданным правилом, может быть построен следующим образом.

Пусть Р31 — проверка условия i<n , где i — текущее, а n — максимальное значение номера обслуживающего канала;

R32 - счетчик числа каналов (реализует операцию i + 1);

P4 — проверка условия где — момент поступле­ния очередной заявки, а — момент освобождения i-ro ка­нала;

F33 - запись в регистр , для которых справедливо усло­вие, проверяемое оператором P4;

K34 - счетчик числа свободных каналов (реализует опера­цию nсв+1, где nсв - число свободных каналов);

Р35 - проверка условия nсв > 0, т. е. имеются ли свободные каналы в момент

F36- реализация заданного правила выборки канала для об­служивания.

Тогда под алгоритм приобретает следующий вид:

(5.76)

Здесь под операторами Р2, A2 и Ф8 условно понимаются про­верка условия , запоминание и формирование = соответственно. Более наглядно сущность работы под алгоритма и его связь с другими частями (операторами) моделирующего алгоритма представлена на рис. 5.4.

Операторы Р31 и К32 обеспечивают перебор всех каналов( i изменяется от 1 до n). Оператор P4 проверяет (для каждого канала) условие , т. е. выясняет, не является ли данный канал свободным в момент . Если условие, проверяемое опе­ратором P4, выполнено, т. е. данный канал в момент занят, то управление передается опять опе­ратору P3. В противном случае ка­нал свободен, и управление пере­дается операторам P33 и K34. Цик­лическая работа под алгоритма про­должается до перебора всех кана­лов (i = n, условие, проверяемое оператором Р33 не выполнено). То­гда управление передается опера­тору P35, который проверяет нали­чие хотя бы одного свободного ка­нала. Если свободные каналы имеются, то переходим к оператору F36 для выбора канала. В против­ном случае в момент свободных каналов нет. Тогда начинаем наби­рать новые до освобождения оче­редного канала.

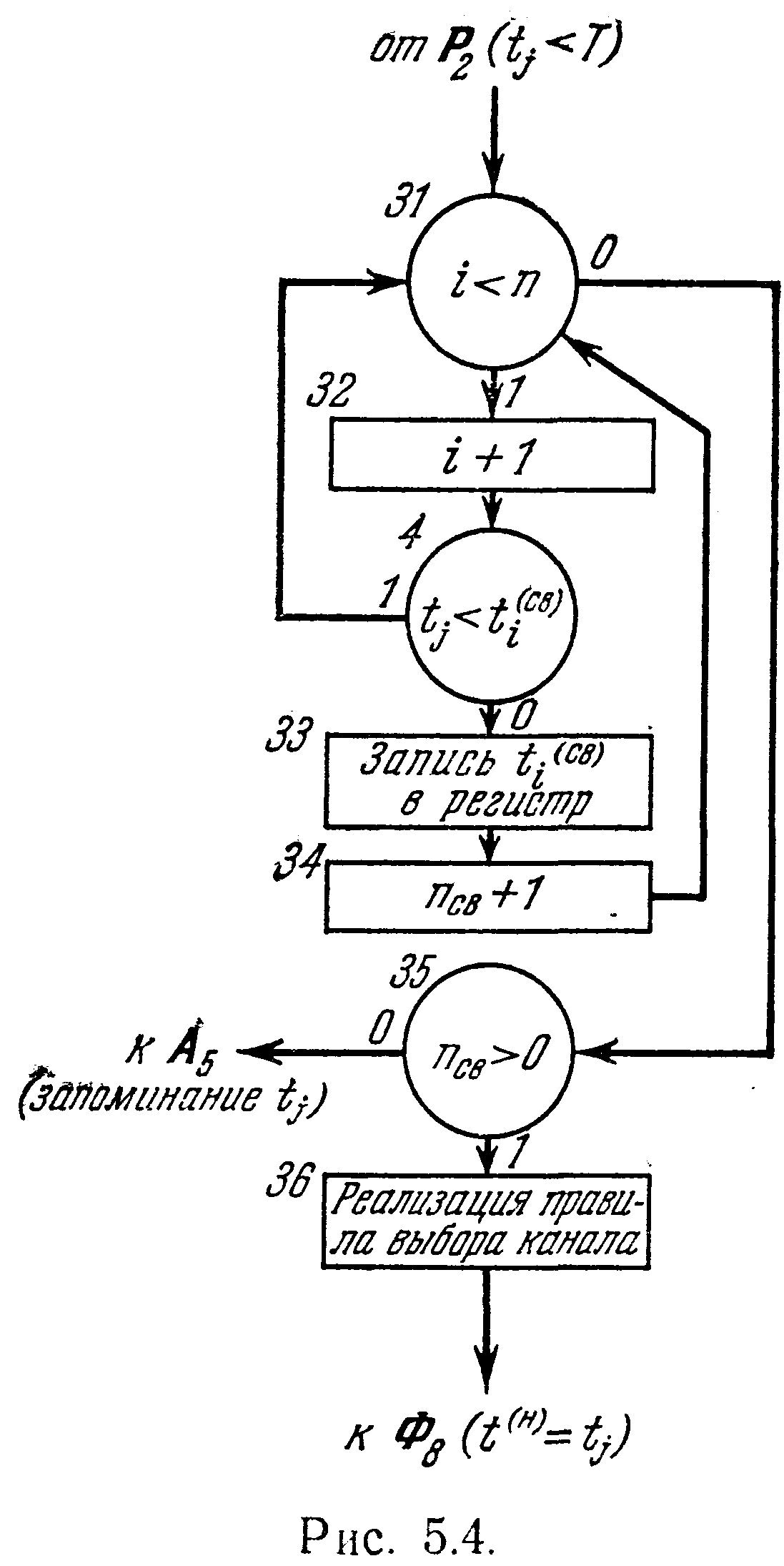
Оператор F36 может реализо­вать практически любое прави­ло выбора канала для обслужива­ния заявки, например: определить min если каналы используются в порядке очереди, выбрать канал по жребию, если они выбираются в случайном порядке, и т.д. В каж­дом конкретном случае под алгоритм (5.76) может иметь тот или другой вид. Например, для условий моделирования, приня­тых в начале настоящего параграфа, он значительно упро­щается (сводится к одному оператору A20—выбору min ) и связывается с другими частями моделирующего алгоритма так, как показано в операторной схеме (5.75).

Рассмотрим еще один пример. Пусть имеется n-канальная система массового обслуживания со свойствами, аналогичными свойствам системы, которую мы рассматривали в начале на­стоящего параграфа (см. моделирующий алгоритм (5.75) и т. д.), за исключением порядка выбора каналов для обслуживания. Пусть теперь каналы выбираются в случайном порядке по жребию.

Операторная схема моделирующего алгоритма для этого слу­чая имеет вид

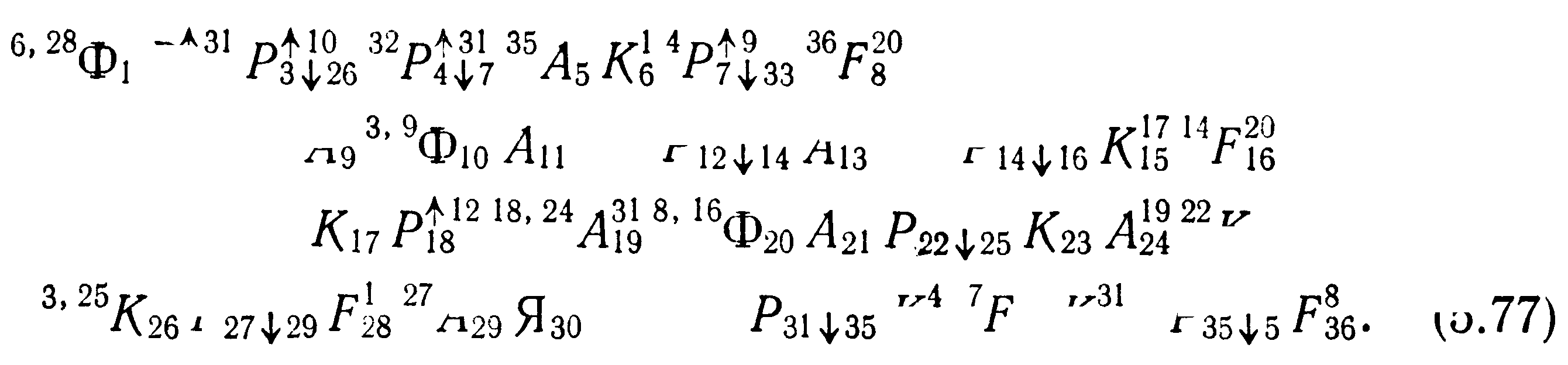(5,77)

Этот же алгоритм в виде блок-схемы представлен на рис. 5.5.

Мы не будем подробно описывать работу алгоритма (5.77), так как отдельные его подалгоритмы уже описаны выше. Сде­лаем некоторые замечания по его структуре. Будем сравнивать рассматриваемый моделирующий алгоритм (5.77) с алгоритмом (5.72), который был достаточно подробно описан в предыдущем параграфе.

Легко видеть, что часть алгоритма (5.77), состоящая из опе­раторов fq, Фзо и т. д. вплоть до выдачи результатов (опера­тор Я30), полностью совпадает с соответствующей частью алго­ритма (5.72) и в дополнительном описании не нуждается. То же самое можно сказать относительно части алгоритма (5.77), со­стоящей из операторов Р7 (при условии, что k > 0) и т. д. вплоть до оператора A19. Она тоже совпадает с соответствую­щей частью алгоритма (5.72). Это обстоятельство можно ин­терпретировать следующим образом. Если нет свободных кана­лов, а очередь заявок имеется (первый случай) или имеется очередь заявок при наличии одной свободной линии (второй случай), то алгоритм (5.77) работает совершенно аналогично алгоритму (5.72). Заметим, что, кроме отмеченных здесь пер­вого и второго случаев, никаких других случаев быть не может (например, не может быть случая, когда одновременно имеется очередь заявок и очередь свободных каналов).

Отличие алгоритма (5.77) от (5.72) начинается с оператора Р7 (когда k=0). Однако необходимо начать рассмотрение с несколько более раннего этапа работы алгоритма. Если (оператор Р2), то управление передается оператору P31. Операторы P31 и K32 обеспечивают просмотр всех каналов. Если условие выполнено (оператор Р4), то данный канал занят в момент tj и управление передается оператору P3 для перехода к следующему каналу. Если же , т. е. условие, проверяемое оператором Р4 не выполнено: в момент tj данный {i-й) канал свободен, — то управление передается оператору P4. Если k > 0 (оператор Р7), то работа алгоритма продолжается по описанному ранее пути: А9, Ф10 и т.д. При k = 0 (оче­реди заявок нет) имеется возможность образования очереди

обслуживающих каналов. Управление передается оператору F33 для записи в регистр момента освобождения канала, способ­ного обслуживать данную заявку. В связи с этим прибавляется единица к числу свободных каналов nсв. Таким образом, отби­раются те каналы, которые оказываются свободными в момент tj. Оператор P35 проверяет наличие свободных каналов. Если таковых нет, то управление передается оператору A5 (аналогия с алгоритмом (5.72)—передача управления от оператора Р4 оператору A5, если }. Когда свободные каналы имеются, работает оператор Р36 (выбор канала по жребию), и управление передается оператору F8 (канал выбран, начинается обслужи­вание заявки).

Таким же образом могут быть построены моделирующие ал­горитмы и для других условий работы многоканальных систем массового обслуживания.

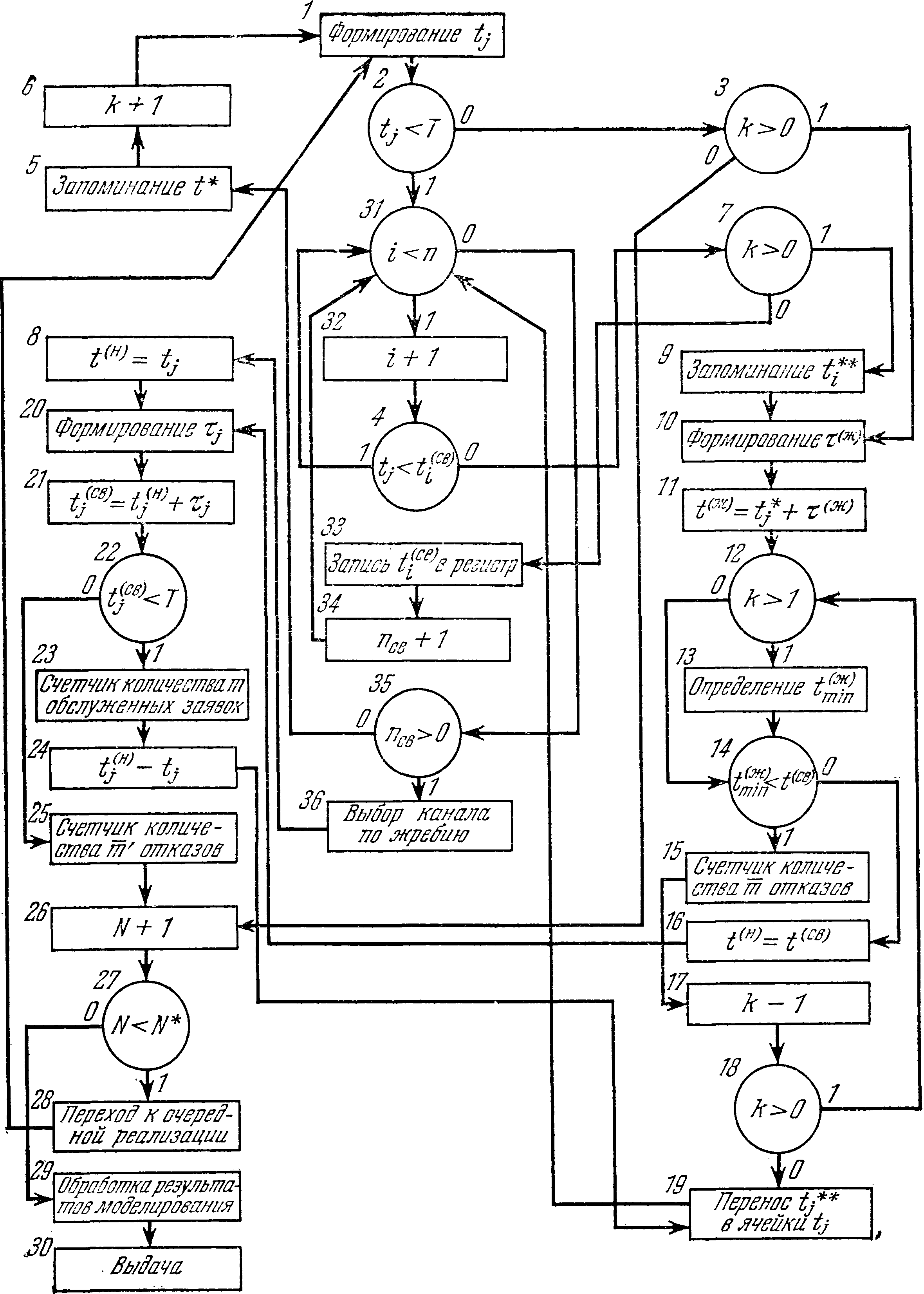
Рис. 5.5.