Одноканальная система.

Моделированию процессов функционирования систем мас­сового обслуживания мы уделяем серьезное внимание по двум соображениям. Во-первых, многие элементы и подсистемы раз­личных сложных систем хорошо описываются как системы мас­сового обслуживания. Поэтому модели типичных систем массо­вого обслуживания представляют непосредственный интерес. Кроме того, приемы моделирования, характерные для систем массового обслуживания, широко используются при построении моделей для сложных систем других типов.

Мы начинаем изучение методики моделирования систем мас­сового обслуживания с простейшего случая системы с одним об­служивающим устройством (каналом).

Итак, рассмотрим одноканальную систему массового обслу­живания, в которую поступают заявки, образующие ординар­ный поток однородных событий с заданным законом распреде­ления. Время занятости канала (длительность обслуживания) является случайной величиной, не зависящей от «предыстории» процесса обслуживания, с законом распределения . Заявки в системе обслуживаются в порядке очереди (в том порядке, в котором они поступили в систему). Если поступившая заявка застает канал занятым, то она ожидает освобождения канала, но не более чем после чего получает отказ. Величина представляет собой случайную величину с законом распределе­ния . Для различных заявок величины независимы.

В результате моделирования желательно получить характе­ристики качества обслуживания: долю обслуженных заявок, долю заявок, получивших отказ, среднее время ожидания и т. д.

Процесс функционирования системы массового обслужива­ния будем рассматривать в интервале времени [0, Т]. Это зна­чит, что заявки, появившиеся в момент tj >T, в модели не рас­сматриваются. Кроме того, обслуженными считаются только те заявки, для которых время окончания обслуживания

Если для данной заявки время начала обслуживания , а время окончания обслуживания , то заявка счи­тается получившей отказ.

Для построения алгоритма, моделирующего процесс функ­ционирования такой системы массового обслуживания, нам по­требуются следующие операторы:

Ф1 - формирование случайных значений моментов tj посту­пления очередной заявки в систему (формирование реализации потока заявок);

Р2 - проверка условия tj < T, где Т — граница интервала времени [0,T], на котором изучается функционирование си­стемы;

Р3 - проверка условия , где момент освобо­ждения канала от обслуживания предыдущей заявки;

Ф4 - формирование случайных значений длительности ожи­дания в соответствии с законом распределения ;

А5 - вычисление верхней границы интервала [ , ] ожидания заявки в очереди;

Р6 - проверка условия <

F7 - формирование момента начала обслуживания j-и за­явки:

F8— формирование момента начала обслуживания j-и за­явки:

Ф9 - формирование случайных значений длительности об­служивания (времени занятости канала) в соответствии с за­коном распределения .

A10 - вычисление момента окончания обслуживания j-и заявки (момента освобождения канала);

Р11 — проверка условия <= T;

K12 — счетчик количества m обслуженных заявок;

A13—вычисление длительности ожидания обслужи­вания (времени пребывания в очереди) для j-и заявки;

K14 — счетчик числа заявок m, получивших отказ;

K15 — счетчик числа реализации N при моделировании;

P16 — проверка условия N < N* , где N* — заданное число реализации, необходимое для обеспечения требуемой точности расчета;

F17 — переход к очередной реализации;

A18—обработка результатов моделирования;

Я19 — окончание вычислений и выдача результатов. Теперь можно записать операторную схему алгоритма, мо­делирующего процесс функционирования рассматриваемой од­ноканальной системы массового обслуживания. Она имеет сле­дующий вид:

(5.69)

Перед началом моделирования должны быть заданы началь­ные условия, соответствующие практической сути дела. Напри­мер, если при t = 0 канал свободен и заявки в систему еще не поступили, то начальные условия будут иметь вид

t0=0, =0, m=0, m=0, N=0 (5.70)

В качестве исходных данных для решения задачи должны быть указаны граница интервала Т исследования процесса, за­кон распределения потока заявок, законы распределения и , а также число реализации N*, обеспечивающее задан­ную точность.

Для наглядности на рис. 5.1 представлена блок-схема мо­делирующего алгоритма, соответствующая операторной схеме (5.69).

Остановимся кратко на работе алгоритма и его основных операторах.

Оператор Ф1 формирует случайные числа, которые имити­руют поток однородных событий tj в соответствии с заданным законом распределения и правилами, рассмотренными в преды­дущем параграфе. Оператор Р2 проверяет условие tj < T. Если

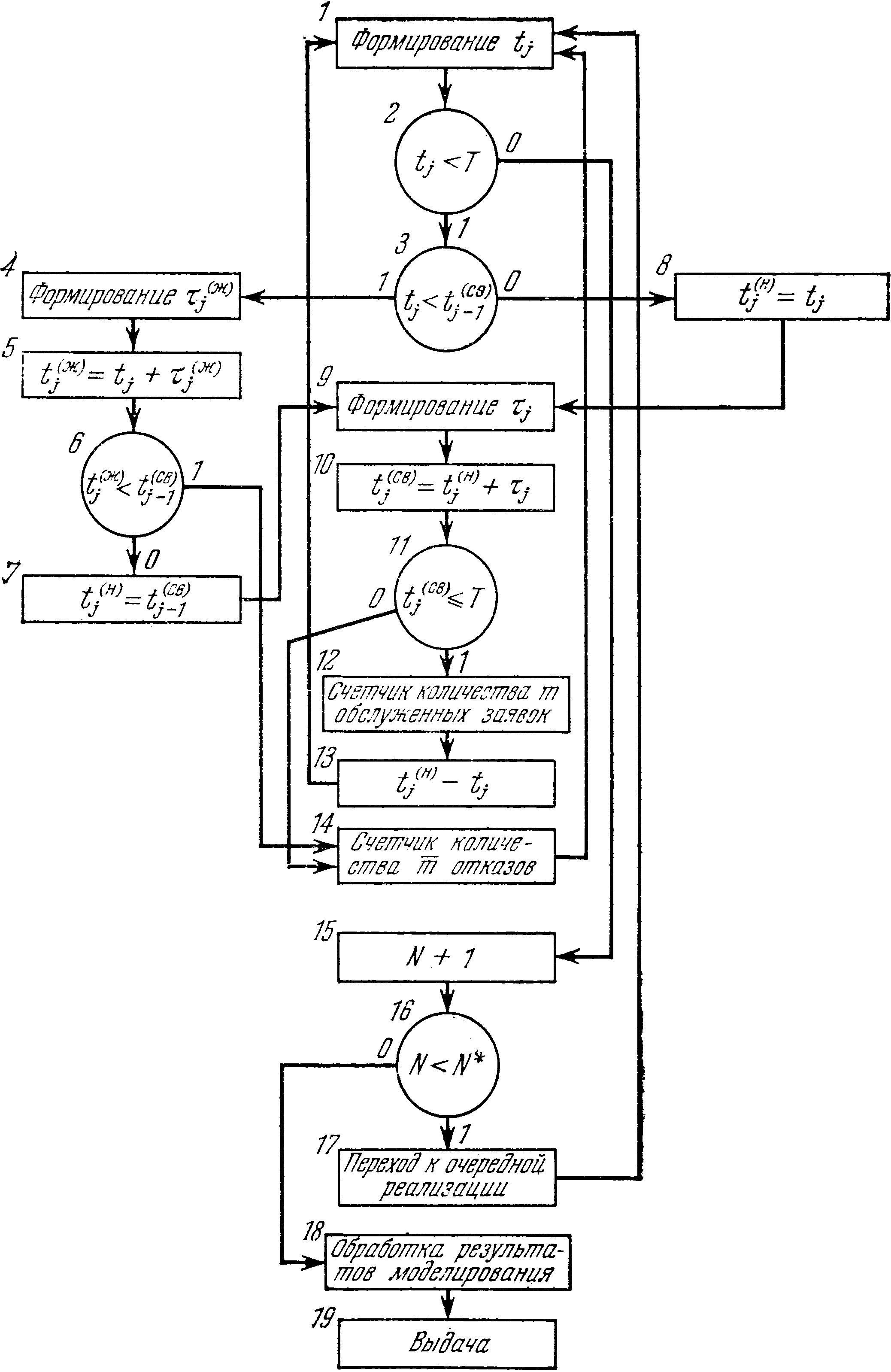
Рис. 5.1.

это условие выполнено, то заявка, появившаяся в момент tj, по­ступает в систему и рассматривается как претендент на об­служивание. Поэтому по стрелке с индексом 1 управление передается оператору Р3 Для дальнейшего оперирования над заявкой. Если же условие, проверяемое оператором P2, не вы­полнено, то заявка в систему в пределах интервала (0,Т) не поступает, и тогда по стрелке с индексом 0 управление пере­дается оператору K15 для подсчета числа реализации.

Оператор Р3 проверяет условие или, другими сло­вами, определяет, занят или свободен канал в момент поступле­ния j-и заявки. Если (в момент поступления заявки ка­нал занят), то управление от оператора Р3 по стрелке с ин­дексом 1 передается оператору Ф4. Рассмотрим сначала эту ветвь алгоритма (Ф4—F7⁷) Оператор Ф4 формирует случайные значения длительности ожидания , оператор А5 вычисляет , а оператор Р6 сравнивает величины и _. Если <= то имеется возможность обслужить заявку, причем момент на­чала обслуживания совпадает с моментом освобождения ка­нала (оператор F7). Если же < , то заявка не может быть обслужена, и тогда от оператора Р6 по стрелке с индек­сом 1 управление передается оператору К14 Для подсчета коли­чества отказов.

Возвратимся к оператору Р3. Пусть теперь в мо­мент поступления заявки канал свободен (условие, проверяемое оператором Рз, оказывается невыполненным). Тогда от опера­тора Р3 по стрелке с индексом 0 управление передается опера­тору F8. Поскольку в момент tj поступления заявки канал сво­боден, обслуживание может быть начато немедленно: = tj

Теперь переходим к работе операторов Ф9 и A10 Они имити­руют сам факт обслуживания заявки (работу обслуживающего канала над заявкой номер j). Одним из операторов F7 или F8 уже определен момент начала операции Оператор Ф9 фор­мирует случайное значение длительности обслуживания а оператор A10 определяет время освобождения канала (момент окончания обслуживания) .

На этом, собственно, заканчивается рассмотрение основной части моделирующего алгоритма. Далее рассматриваются опе­раторы, хотя и не имеющие отношения к имитации работы об­служивающего канала, но играющие существенную роль при моделировании.

Оператор Р11 проверяет условие <= T. Если это условие выполнено, то весь интервал времени, в течение которого про­должалось обслуживание заявки, принадлежит интервалу [0, Т].Поэтому рассматриваемую заявку можно считать обслуженной. От оператора Р11 по стрелке с индексом 1 управление пере­дается оператору К12 для подсчета количества обслуженных за­явок. Далее вступает в строй оператор A13, который вычисляет для рассматриваемой обслуженной заявки время ее пребывания в системе (время ожидания в очереди). Эта ве­личина может оказаться необходимой для формирования одной из искомых величин (например, среднего времени ожидания при обработке результатов моделирования (оператор А18)).

От оператора А13 управление передается оператору Ф1 для формирования момента поступления новой заявки.

Если же > T (возвращаемся к оператору Р11), то окон­чание обслуживания не помещается в интервале [0,T], и мы должны считать, что заявка получает отказ. В связи с этим от оператора Р11 по стрелке с индексом 0 управление передается оператору K14 для подсчета числа отказов и, поскольку история данной заявки закончилась, далее оператору Ф1 для формиро­вания момента поступления новой заявки.

В связи с рассмотрением работы оператора Р3 мы уже отме­чали, что при невыполнении условия очередная заявка на обслуживание не поступает, заканчивается соответствующая реализация процесса обслуживания, и управление от оператора Р2 (по стрелке с индексом 0) передается оператору К15. Опера­тор К15 прибавляет единицу к количеству обследованных реали­заций процесса. Полученное число N сравнивается (оператор P16) с N*, и если N < N*, то моделирование продолжается (опе­раторы F17, Ф1 b т.д. ), в противном случае моделирование за­канчивается (операторы A18 и Я19).

Обработка результатов моделирования предусматривает ис­пользование сведений, накопленных счетчиками К12 (число об­служенных заявок), K14 (число отказов), а также оператором А13 (длительность пребывания заявки в системе), для оценки искомых величин (вероятность отказа, среднее время ожидания и т. д.).

Иногда требуется знать вероятностные характеристики дли­ны очереди (числа заявок в очереди). В рассмотренном нами моделирующем алгоритме не предусмотрена фиксация такой информации, которая позволила бы оценить эти характеристики. Однако модификация алгоритма, обеспечивающего фиксацию такой информации, оказывается несложной. Для этого доста­точно фиксировать следующие события: поступление новой за­явки в систему, начало обслуживания очередной заявки и уход из системы заявки, получившей отказ.