Оглавление

Системы массового обслуживания. 3

Формирование реализации случайных потоков однородных событий 10

Одноканальная система. 14

Простейшая многоканальная система. 19

Точность и вероятность в имитации СМО 24

Алгоритм имитации работы СМО 24

Описание Процедур и Функций. 25

Текст программы. 25

Результат работы программы. 27

Список использованной литературы. 30

Системы массового обслуживания.

Для решения многих прикладных задач можно ограничиться частными случаями потоков, оперирование которыми оказы­вается более простым и доступным. К такого рода потокам од­нородных событий относятся так называемые потоки с ограни­ченным последействием.

Случайный поток однородных событий называется потоком с ограниченным последействием, если случайные величины являются независимыми.

Очевидно, что для потоков с ограниченным последействием совместная функция

плотности f(z1, z2 ..., zk) представляется в виде

(5.3)

Функции fj{Zj) при j>1 являются функциями плотности ве­личин .

Большой теоретический и практический интерес представ­ляют так называемые стационарные потоки, для которых ве­роятностный режим не зависит от времени.

Более точно: поток однородных событий называется стацио­нарным, если вероятность Pk(t, t0) появления k событий за про­межуток времени (t0, t0 + t) не зависит от to, а зависит только от t и k.

Для стационарных потоков с ограниченным последействием имеет место соотношение

(5.4)

Это значит, что при j>1 интервалы одинаково распре­делены.

Рассмотрим математическое ожидание случайной вели­чины при j>1:

Величина имеет смысл средней длины интервала между последовательными заявками.

Легко видеть, что для стационарных потоков с ограниченным последействием величина

(5.5)

имеет смысл среднего Количества событий, наступающих за еди­ницу времени. Параметр носит название плотности или интен­сивности потока.

В качестве примера стационарного потока с ограниченным последействием можно привести поток с равномерным распре­делением интервалов времени между заявками. Функция плот­ности f(z) в этом случае имеет вид

(5.6)

Поскольку математическое ожидание величины равно b/2. то плотность потока, задаваемого функцией плотности (5.6), равна

(5.7)

Для стационарных потоков с ограниченным последействием имеет место соотношение (формула Пальма, см. [30, 38, 60]), связывающее функции плотности f1(z1) и Ошибка! Ошибка связи.:

(5.8)

Пользуясь (5.8), можно получить функцию плотности f1(z1) для различных стационарных потоков с ограниченным после­действием. Например, для потока с равномерным распределе­нием интервалов

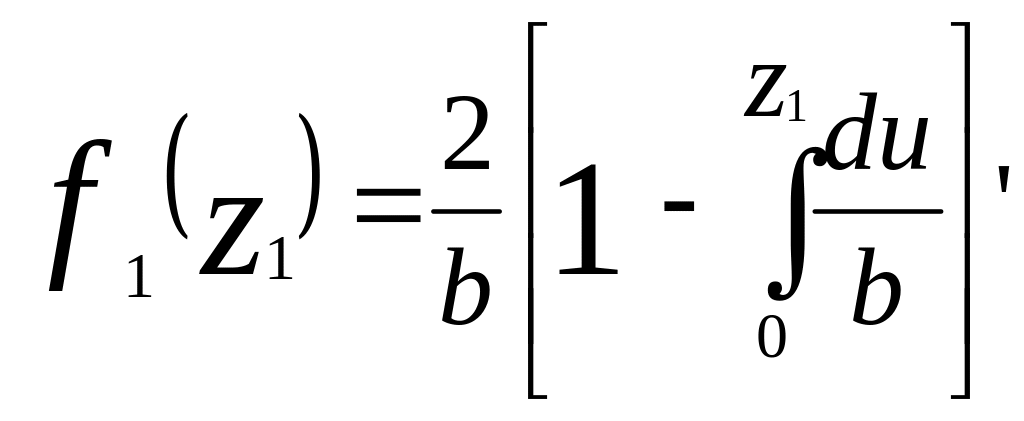(5.9)

ИЛИ

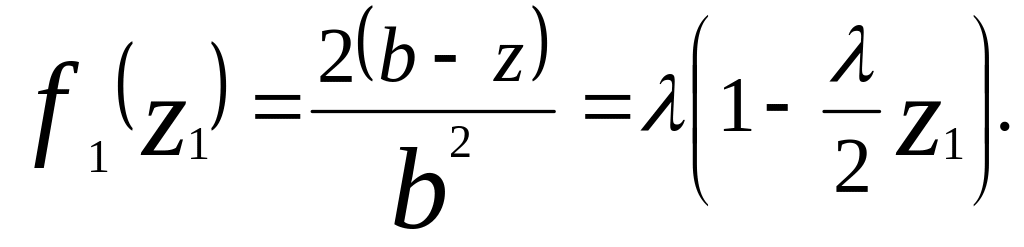
Легко видеть, что математическое ожидание первого интервала для потока (5.6) равно

(5.10)

Случайный поток однородных событий с равномерным рас­пределением интервалов времени между последовательными за­явками часто используется для решения различных задач, воз­никающих на практике.

До сих пор рассматривались так называемые ординарные по­токи однородных событий. Поток называется ординарным, если вероятность появления двух и более событий за проме­жуток времени (to, to + t) при любом to является бесконечно малой величиной по сравнению с t, т. е.

Ознакомившись с методами математического описания пото­ков однородных событий, можно перейти к формальному пред­ставлению процессов функционирования самих систем массо­вого обслуживания.

Пусть система массового обслуживания состоит из п линий, способных одновременно обслуживать заявки. В любой момент времени линия находится в одном из двух состояний — линия свободна или линия занята.

Предположим, что в некоторый момент времени в обслужи­вающую систему поступает заявка. Если в этот момент времени имеются свободные линии, то заявка принимается к обслужи­ванию. В противном случае, т. е. когда все линии заняты, за­явка остается в системе в течение некоторого времени ( - время пребывания заявки в системе) как претендент на обслу­живание. За интервал времени заявка должна быть принята к обслуживанию, в противном случае она считается потерянной (получает отказ).

В зависимости от величины системы массового обслужи­вания делятся на три существенно различных класса, имеющих свою специфику как в строении процесса обслуживания, так и в математической формулировке относящихся к ним задач.

Если = 0, то поступившая в данный момент времени за­явка либо немедленно принимается к обслуживанию, если имеются свободные линии, либо получает отказ, если все линии заняты. Такие системы массового обслуживания называются системами с отказами. Для систем с отказами показателями качества обслуживания обычно считаются вероятность от­каза, среднее число отказов заданный интервал времени и т.д.

В другом крайнем случае, когда , поступающие в си­стему заявки отказов не получают, а ожидают (если все линии заняты) в очереди до того момента, когда они будут приняты к обслуживанию. Такого рода системы массового обслуживания называются системами с ожиданием. Показателями качества обслуживания в этом случае могут быть среднее время ожида­ния заявки, средняя длина очереди и т. д.

Наконец, если, заявка, заставшая все линии за­нятыми в момент поступления, ожидает в течение в очереди, а по истечении этого времени получает отказ. Такие системы массового обслуживания называются системами с ограничен­ным ожиданием. Качество обслуживания в этом случае оцени­вается вероятностными характеристиками как количества от­казов, так и времени ожидания, а иногда более сложными показателями, учитывающими обе эти стороны качества обслу­живания.

Помимо параметра для характеристики свойств обслужи­вающей системы необходимо задать также - время обслужи­вания заявки, или, как его иначе называют, время занятости ли­нии. Заявка, принятая к обслуживанию, занимает одну из линий на время ; по истечении этого времени линия освобождается и может приступить к обслуживанию новой заявки.

Обычно величины и считаются случайными величинами с заданными законами (или совместным законом) распределе­ния. Иногда предполагают, что одна из них или обе фиксиро­ваны.

Перейдем к рассмотрению распространенных вариантов по­рядка занятия линии заявками, поступающими на обслужива­ние. Если в системе массового обслуживания имеется очередь заявок, то освобождающиеся линии занимаются немедленно в порядке их освобождения. В случае, когда очереди заявок нет, и имеются свободные линии, появившаяся заявка может зани­мать одну из свободных линий в соответствии со специальными правилами. Наиболее часто на практике используются следую­щие правила.

1. Линии занимаются в порядке их номеров. Линия с боль­шим номером не может быть привлечена к обслуживанию за< явки, если имеется свободная линия с меньшим номером.

2. Линии занимаются в порядке очереди. Освободившаяся линия поступает в очередь и не начинает обслуживания заявок до загрузки всех ранее освободившихся линий.

3. Линии занимаются в случайном порядке в соответствии с заданными вероятностями. Если в момент поступления очере­дей заявки имеется свободных линий, то в простейшем слу­чае вероятность занять некоторую определенную линию может быть принята равной . В более сложных случаях ве­роятности p1,p2,…,pn занять линию считаются зависящими от номеров линий, моментов их освобождения и других пара­метров.

Аналогичные предположения могут быть сделаны и относи­тельно порядка принятия заявок к обслуживанию в том случае, когда в системе образуется очередь заявок.

1. Заявки принимаются к обслуживанию в порядке очереди. Освободившаяся линия приступает к обслуживанию той заявки, которая ранее других поступила в систему.

2. Заявки принимаются к обслуживанию по минимальному времени получения отказа. Освободившаяся линия приступает к обслуживанию той заявки, которая в кратчайшее время может получить отказ.

3. Заявки принимаются к обслуживанию в случайном по­рядке в соответствии с заданными вероятностями. Если в мо­мент освобождения линии имеется т заявок в очереди, то в про­стейшем случае вероятность выбрать для обслуживания неко­торую определенную заявку может быть принята равной q = 1/m. В более сложных случаях вероятности q1,q2,…,qm считаются зависящими от времени пребывания заявки в системе, времени, остающегося до получения отказа, и других параме­тров.

Перечисленными предположениями, естественно, охваты­ваются не все случаи, возникающие на практике, а лишь наи­более распространенные.

Реальный процесс функционирования системы массового об­служивания для удобства исследования следует представлять в виде последовательности отдельных актов (фаз) обслужива­ния, выполняемых различными устройствами. При этом, как правило, соблюдается такой порядок, при котором следующее устройство может приступить к обслуживанию заявки лишь тогда, когда работа предыдущего с данной заявкой полностью закончена.

В частном случае обслуживание может быть однофазным. Простейшим примером многофазного обслуживания являет­ся обслуживание покупателей в магазине. Сначала покупатель занимает одного из работников прилавка, демонстрирующего товары и оформляющего товарные чеки (первая фаза). Отобрав товары и получив чек, покупатель должен пройти через вторую фазу — оплатить чек в кассе. И только с оплаченным чеком по­купатель может быть принят на обслуживание в отдел контроля и выдачи покупок (третья фаза).

Более сложным примером многофазного обслуживания мо­жет служить технологический процесс, связанный с последова­тельной обработкой изделий при помощи оборудования различ­ного назначения. Изделие может поступить на обработку стан­ком n+1-й фазы лишь тогда, когда его обработка на станке п-и фазы закончена.

Весьма распространенным типом обслуживания является об­служивание с преимуществом (с приоритетом) [33]. Каждой за­явке, поступающей в систему, приписывается некоторый коэф­фициент преимущества (приоритет). При этом могут быть раз­личные варианты дисциплины очереди. При одном из вариантов в момент освобождения канала на обслуживание поступает за­явка из очереди, у которой коэффициент преимущества наи­больший.

При другом варианте дисциплины очереди с преимущест­вами возможно прекращение обслуживания заявки, занимаю­щей канал, если в систему поступила заявка с большим значением коэффициента преимущества, чем у обслуживаемой заявки.

Примером систем массового обслуживания с преимущест­вом может служить доставка телеграмм: в первую очередь до­ставляются телеграммы типа «молния», затем срочные и в по­следнюю очередь обыкновенные.

Рассмотрев основные модификации процесса функциониро­вания систем массового обслуживания, перейдем к вопросу о величинах, которые являются искомыми при решении задач, связанных с массовым обслуживанием (показатели качества обслуживания).

Для системы с отказами наиболее широко используемым по­казателем качества обслуживания является средняя доля отка­зов R (to, t) за промежуток времени (to, to+t). Эта величина определяется следующим образом.

Рассмотрим совокупность независимых реализации процесса обслуживания на интервале (tо, to+t). Количество заявок, по­ступивших на обслуживание за этот интервал времени для вы­бранной наудачу реализации, будет случайной величиной Ni(to, t). Пусть N(to,t) - среднее количество заявок, поступаю­щих на обслуживание в течение интервала времени (to,to+t). Количество заявок mi(to,t), Получивших отказ в течение того же интервала времени, также будет случайной величиной. Ее математическое ожидание m(fo, t) является средним количе­ством отказов за интервал времени (to, to+t). Тогда средняя доля отказов R(to, t) определяется как

Кроме средней доли отказов R (to, t) как показатель каче­ства обслуживания иногда используется вероятность P0(to, t) того, что за время (to, to + t) не будет ни одного отказа.

В случае стационарного входного потока величина N(to, t) не зависит от to и равна

(5.37)

где - интенсивность потока заявок.

Для систем обслуживания с постоянными параметрами и мо­ментов времени, достаточно удаленных от начала обслужива­ния, величина m(to, t) также не зависит от to и может быть вы­ражена соотношением, аналогичным (5.37):

где — интенсивность потока отказов.

Тогда средняя доля отказов R равна постоянной величине

не зависящей от длительности интервала времени t. В связи с соотношением (5.39) величина R имеет также смысл вероят­ности отказа для заявки, поступившей в систему в произволь­ный момент времени.

Для систем с ожиданием показателями качества обслужива­ния могут быть среднее значение времени ожидания или сред­нее значение длины очереди (количество заявок, ожидающих обслуживания). Иногда используются и другие параметры за­кона распределения времени ожидания или длины очереди.

Для смешанных систем показателями качества обслужива­ния служат как те, так и другие величины.

Известные (см. [30, 33, 38, 42, 55, 60] и др.) аналитические соотношения теории массового обслуживания, связывающие ха­рактеристики потока заявок и параметры системы с показате­лями качества обслуживания, обычно представляют собой асим­птотические формулы, дающие значения показателей для моментов времени, достаточно удаленных от начала обслужива­ния. Такие формулы имеются, главным образом, для случая, когда заявки образуют простейший (пуассоновский) поток од­нородных событий, а обслуживание является однофазным.

В качестве примера такого рода асимптотических формул можно привести формулу Эрланга (см., например, [60]).

Рассмотрим однофазную систему с отказами ( = 0), со­стоящую из n линий. Для обслуживания поступившей заявки линии выбираются в случайном порядке с одинаковыми вероят­ностями. Время занятости линии (время обслуживания) являет­ся случайной величиной, не зависящей от «предыстории» про­цесса обслуживания, с конечным математическим ожиданием .

Предположим, что в такую систему поступает простейший поток заявок с интенсивностью .

Тогда асимптотическое (при ) значение вероятности отказа R может быть определено по формуле

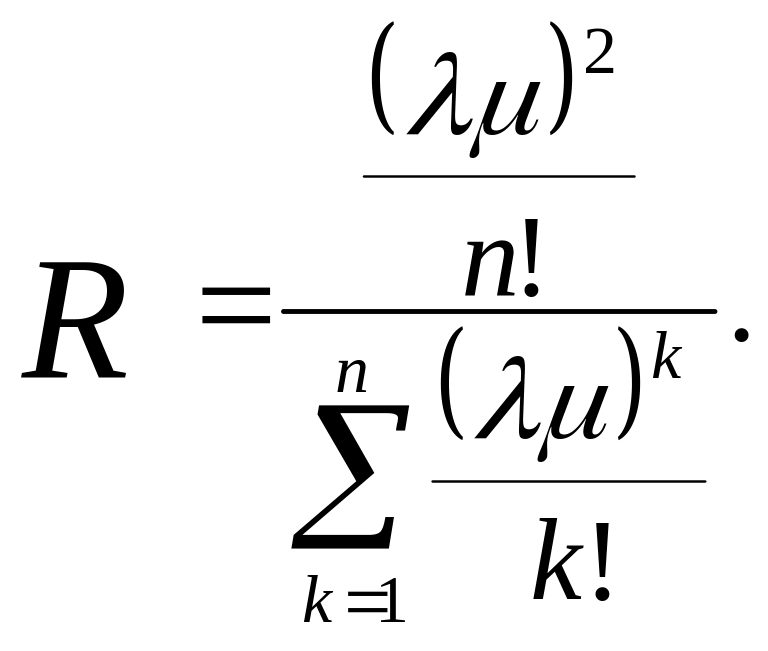(5.40)

Рассмотренная схема обслуживания является одной из наи­более элементарных. Для других схем соответствующие фор­мулы оказываются более сложными; они рассматриваются в упоминавшейся выше литературе по теории массового обслу­живания.

Для многих прикладных задач предположения, при которых справедливы такие формулы, оказываются слишком стеснитель­ными. При решении задач методом имитационного моделирова­ния некоторые предположения могут быть существенно ослаб­лены. Например, можно рассматривать обслуживающие си­стемы, состоящие из нескольких последовательно действующих, в общем случае, не однотипных устройств.

Другим важным обобщением задачи является предположе­ние о характере потока заявок, поступающих на обслуживание. Допускаются потоки однородных событий с практически произ­вольным законом распределения. Последнее обстоятельство ока­зывается существенным по следующим двум причинам. Во-пер­вых, реальные потоки заявок в некоторых случаях заметно отличаются от простейшего. Для пояснения второй причины пред­положим, что исходный поток заявок достаточно точно аппро­ксимируется простейшим потоком. При этом поток заявок, об­служенных на первой фазе, уже, вообще говоря, не будет про­стейшим. Поскольку поток, являющийся выходным для первой фазы, будет входным потоком для линий, обслуживающих заяв­ки на второй фазе, мы снова приходим к задаче обслуживания потоков, не являющихся простейшими.

В качестве следующих обобщений задачи будем рассматри­вать схемы обслуживания с произвольными предположениями относительно порядка привлечения линий и выбора заявок, а также судьбы заявок, обслуживаемых линиями, выходящими из строя по причине неабсолютной надежности.

Ряд существенных обобщений постановки задачи будет рас­смотрен в конце настоящей главы.

Сущность метода имитационного моделирования примени­тельно к задачам массового обслуживания состоит в следую­щем. Строятся алгоритмы, при помощи которых можно выра­батывать случайные реализации заданных потоков однородных событий, а также моделировать процессы функционирования обслуживающих систем. Эти алгоритмы используются для мно­гократного воспроизведения реализации случайного процесса обслуживания при фиксированных условиях задачи. Получае­мая при этом информация о состоянии процесса подвергается статистической обработке для оценки величин, являющихся по­казателями качества обслуживания.

Метод имитационного моделирования позволяет более полно, по сравнению с аналитическими формулами, исследовать зави­симость качества обслуживания от характеристик потока за­явок и параметров обслуживающей системы.

С одной стороны, при решении задач теории массового об­служивания методом моделирования может быть использована более обширная информация о процессе, чем это обычно удает­ся сделать, применяя аналитические методы. С другой стороны, значения показателей качества обслуживания, получаемые из аналитических формул, обычно относятся к моментам времени, достаточно удаленным от начала процесса. Реально, для момен­тов времени, близких к началу процесса, когда еще не наступил стационарный режим, значения показателей качества обслужи­вания в общем случае существенно отличаются от асимптотиче­ских значений. Метод имитационного моделирования позволяет достаточно обстоятельно изучать переходные режимы.

Перейдем к краткому изложению методики моделирования процессов массового обслуживания на цифровых машинах уни­версального назначения. В первую очередь рассмотрим спо­собы формирования реализации случайных потоков однородных событий, используемых при моделировании процессов обслу­живания.