3.2 Диагностирование продольной силы и момента инерции массы балки.

Рассмотрим теперь обратную задачу диагностирования продольной силы и момента инерции по заданным частотам колебаний системы.

Обратная задача. Известны собственные частоты колебаний механической системы балки. Неизвестны продольная сила и момент инерции балки.

Рассмотрим метод решения обратной задачи. Если даны две собственные частоты и , то подставляя их в уравнение (1.33), получим снова систему алгебраических уравнений (3.2) с двумя неизвестными , .

Вычитая из первого уравнения системы (3.2) второе уравнение, имеем:

.

(3.5)

Откуда выразим продольную силу :

(3.6)

Подставляя значение (3.6) для продольной силы в первое уравнение системы (3.2), получим:

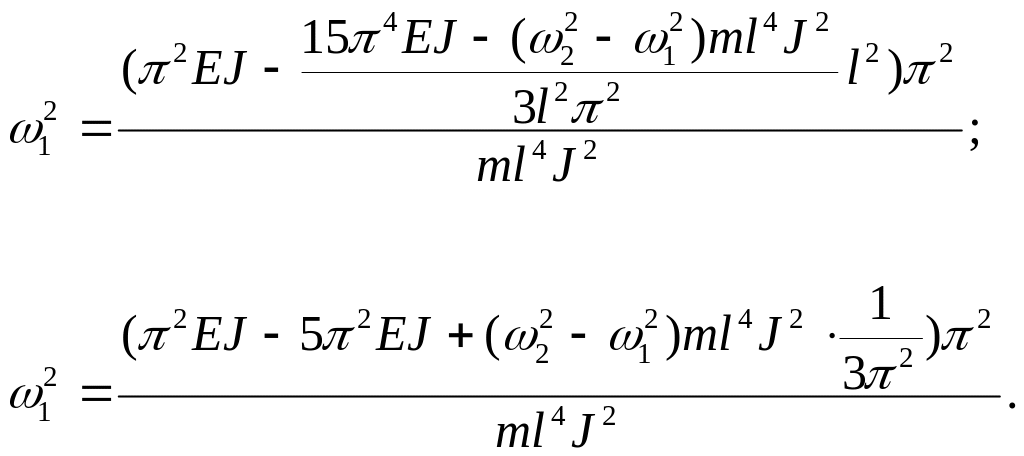
Раскрываем скобки:

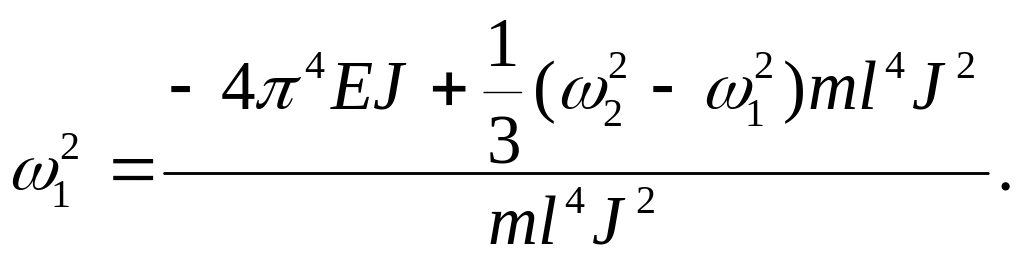
После преобразований выразим момент инерции :

(3.7)

Таким образом, по известным двум частотам колебаний балки с помощью формул (3.6) и (3.7) можно определить продольную силу и момент инерции балки.

Пример 3. Известны следующие физические параметры механической системы и частоты колебаний и :

Найти продольную силу и момент инерции балки.

Решение.

Система уравнений (3.2) после подстановки в него заданных числовых значений принимает вид:

Решение системы, найденное с помощью ЭВМ:

Эти же значения определяются по аналитическим формулам (3.6) и (3.7).

Действительно, если заданные значения частот , и физические характеристики подставить в равенство (3.7), получим:

Найденное значение момента инерции балки, подставим в формулу (3.6):

Таким образом, по формулам (3.6) и (3.7) определены такие же значения продольной силы и момента инерции:

Заметим снова, что искомые характеристики определены верно, так как по решению прямой задачи именно этим значениям и соответствуют заданные значения собственных частот.

3.3 Программная реализация решения обратной задачи

Решение обратной задачи выполнено в среде Maple 12⁹. Программа позволяет по заданным частотам балки под действием продольной силы.

Были использованы следующие команды математического пакета Maple 12¹⁰:

• Simplify, которая предназначена для упрощения разнообразных выражений, включающих рациональные дроби (алгебраические выражения);

• Collect, приводит подобные члены в обобщенных полиномах нескольких переменных, в которых в качестве неизвестных могут выступать функции с аргументами, являющимися неизвестными величинами;

• Solve, решение нелинейных уравнений в системе Maple, выдает решение в аналитическом виде;

• Restart, данная команда очищает от старого смысла и значений все переменные.

Листинг программы с комментариями:

> restart; with(LinearAlgebra):

> W:=solve(sqrt(N/(E*J*2)+sqrt(N^2/(E^2*J^2*4)+(m*w^2)/E*J))*l=pi*n,w^2);

Warning, solving for expressions other than names or functions is not recommended.

Находим w^2 (квадрат частоты)

> w:=W;

> n:=1;N:=10;l:=4;J:=1.84*10^(-5);E:=2.1*10^8;m:=150;pi:=3.14;

Находим квадрат частоты w1

> w1:=w;

Находим саму частоту w1

> W1:=sqrt(w1);

> n:=2;N:=10;l:=4;J:=1.84*10^(-5);E:=2.1*10^8;m:=150;pi:=3.14;

Находим квадрат частоты w2

> w2:=w;

Находим саму частоту w2

> W2:=sqrt(w2);

> n:=3;N:=10;l:=4;J:=1.84*10^(-5);E:=2.1*10^8;m:=150;pi:=3.14;

Обратная задача: (неизвестны , ) решаем через известные 2 частоты:

> w:='w'; m:='m';l:='l';

> w:=w1; eq11:=evalf(w=pi^2*1^2*(-N*l^2+pi^2*1^2*E*J)/m/J^2/l^4);

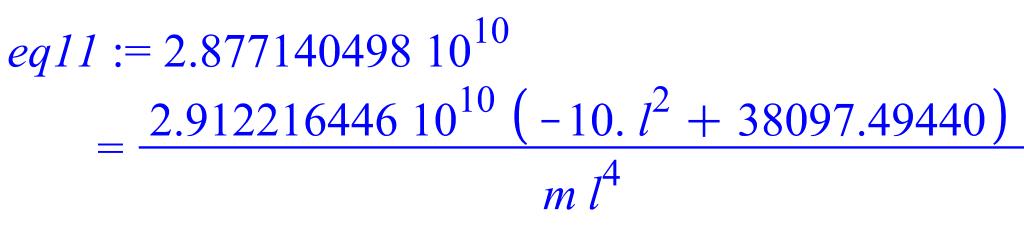
> w:=w2; eq12:=evalf(w=pi^2*2^2*(-N*l^2+pi^2*2^2*E*J)/m/J^2/l^4);

> solve({eq11,eq12},{m,l});

Обратная задача: (неизвестны , ) решаем через известные 2 частоты:

> w:='w'; N:='N'; J:='J';

> w:=w1; eq11:=evalf(w=pi^2*1^2*(-N*l^2+pi^2*1^2*E*J)/m/J^2/l^4);

> w:=w2; eq12:=evalf(w=pi^2*2^2*(-N*l^2+pi^2*2^2*E*J)/m/J^2/l^4);

> solve({eq11,eq12},{N,J});