2 Влияние характеристик балки на собственные частоты ее изгибных колебаний

2.1 Влияние массы балки на частоты ее колебаний

Из уравнения (1.33) при конкретных значениях параметров балки под действием продольной силы можно определить значения собственных частот колебаний балки.

_{Рассмотрим влияние массы балки на значения собственных частот колебаний. Для этого будем менять массу балки, оставляя другие физические параметры неизменными.}

По решению задачи получаем, что при увеличении массы m балки частоты колебаний уменьшаются.

Рассмотрим, например, следующие физические параметры системы:

.

(2.1)

В таблице 1 указаны значения собственных частот колебания балки, соответствующие увеличивающимся значениям массы m и при параметрах (2.1) механической системы.

Таблица 1 – Зависимость частот от массы m при параметрах (2.1) механической системы

150	1,6962	6,7956	15,2945
170	1,5933	6,3833	14,3666
190	1,5071	6,038	13,5895
210	1,4336	5,7433	12,9262
230	1,3698	5,4879	12,3514

На рисунках 4-6 даны графики зависимостей собственных частот , , от массы m балки для рассматриваемой выше задачи.

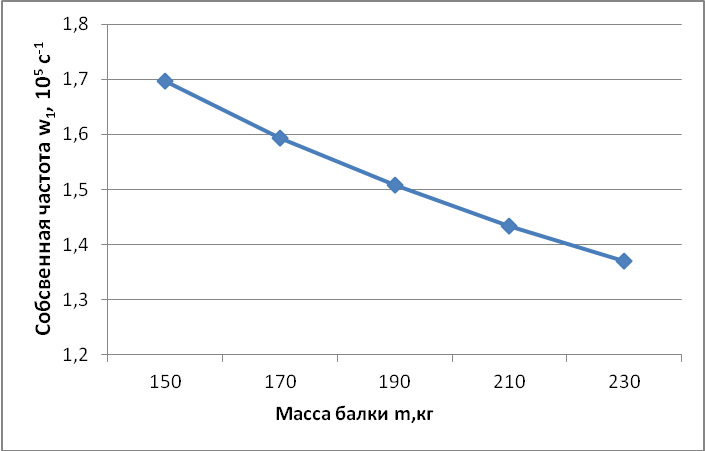
Рисунок 4 – Зависимость частоты от массы m балки при параметрах (2.1) системы

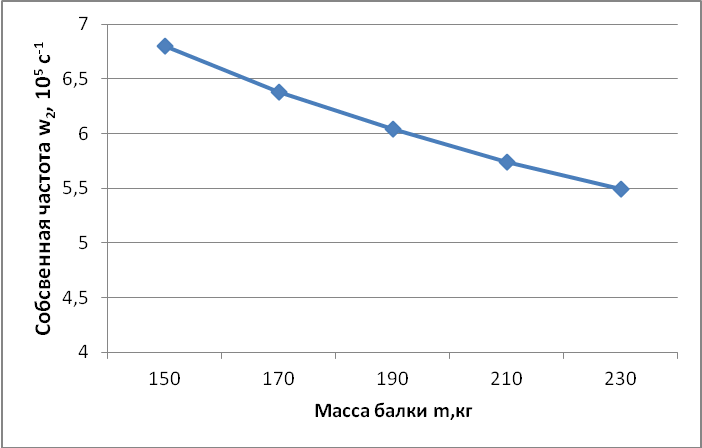
Рисунок 5 – Зависимость частоты от массы m балки при параметрах (2.1) системы

Рисунок 6 – Зависимость частоты от массы m балки при параметрах (2.1) системы

Таким образом, увеличение массы балки m ведет к уменьшению частот его колебаний.

2.2 Зависимость частот колебаний балки от ее длины

_{Рассмотрим теперь влияние длины балки на значения собственных частот колебаний. Будем менять длину балки и определять соответствующие им значения собственных частот.}

По решению прямой задачи получаем, что при увеличении длины балки, частоты колебаний уменьшаются. Рассмотрим, например, следующие параметры системы:

.

(2.2)

В таблице 2 указаны значения собственных частот колебания балки, соответствующие увеличивающимся значениям длины l и при параметрах (2.2) механической системы.

Таблица 2 – Зависимость частот от длины l при параметрах (2.2) механической системы

4	1,6962	6,7956	15,2945
5	1,0842	4,3478	9,7872
6	0,0751	3,0182	6,7955
7	0,0551	2,2165	4,9917
8	0,0421	1,6962	3,8209

На рисунках 7-9 даны графики зависимостей собственных частот , , от длины l балки для рассматриваемой выше задачи.

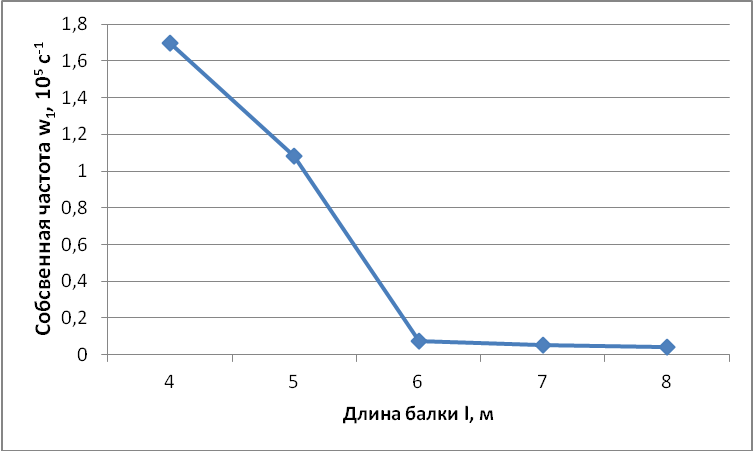
Рисунок 7 – Зависимость частоты от длины l балки при параметрах (2.2) системы

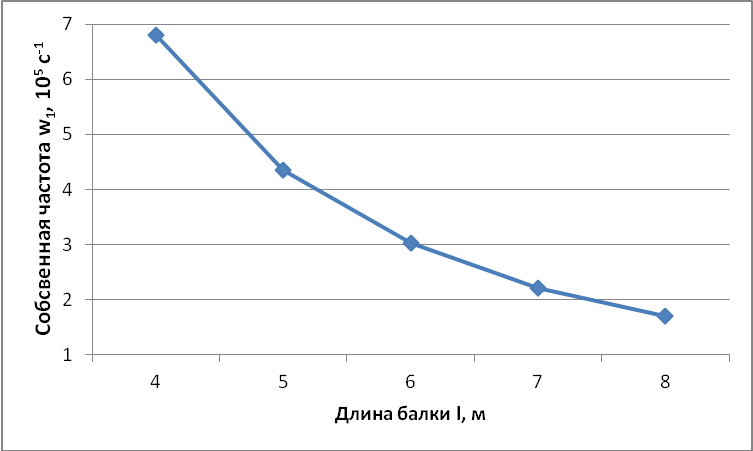
Рисунок 8 – Зависимость частоты от длины l балки при параметрах (2.2) системы

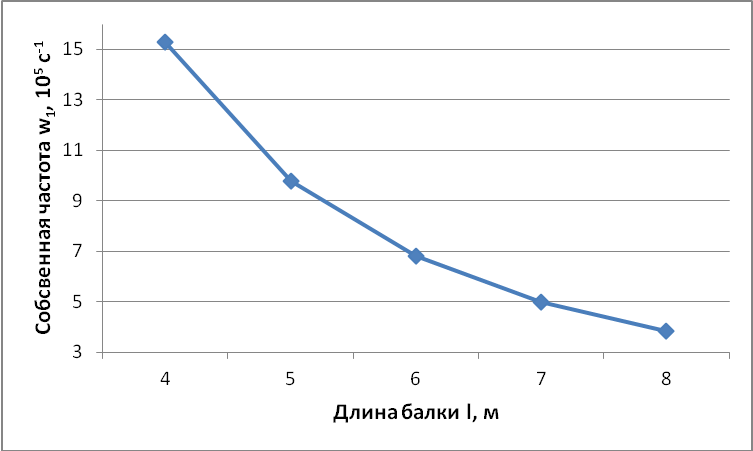
Рисунок 9 – Зависимость частоты от длины l балки при параметрах (2.2) системы

Таким образом, увеличение длины балки l ведет к уменьшению частот его колебаний.