1.2 Основное уравнение колебаний балки. Граничные условия

Из теории свободных колебаний механических систем известны следующие дифференциальные зависимости при изгибе балок:

,

(1.6)

.

(1.7)

Здесь – жесткость при изгибе, – прогиб, – изгибающий момент, q – интенсивность распределенной нагрузки.

Объединяя (1.6) и (1.7), получим:

.

(1.8)

В задаче о свободных колебаниях, нагрузкой для упругого скелета являются распределенные силы инерции:

,

(1.9)

где m – интенсивность массы балки (масса единицы длины), и уравнение (1.8) принимает вид:

.

В частном случае постоянного поперечного сечения, когда , , имеем:

.

(1.10)

Для решения уравнения (1.10) полагаем, что:

.

(1.11)

Подставляя (1.11) в (1.10), приходим к уравнению:

.

Для тождественного выполнения этого равенства необходимо, чтобы каждая из частей равенства была постоянной. Обозначая эту постоянную через , получим два уравнения:

.

(1.12)

.

(1.13)

Первое уравнение указывает на то, что движение носит колебательный характер с частотой . Второе уравнение определяет форму колебаний. Решение уравнения (1.13) содержит четыре постоянных и имеет вид:

,

где

.

(1.14)

Удобно использовать вариант записи общего решения, предложенный А.Н. Крыловым:

.

(1.15)

Здесь:

(1.16)

представляют собой функции А.Н. Крылова⁸.

Заметим, что при . Функции S, T, U, V связаны между собой следующим образом:

(1.17)

Поэтому производные выражения (1.15) записываются в виде:

(1.18)

В задачах рассматриваемого класса число собственных частот бесконечно велико; каждой из них отвечает своя функция времени и своя фундаментальная функция . Общее решение получится путем наложения частных решений вида (1.11):

.

(1.19)

Для определения собственных частот и формул необходимо рассмотреть граничные условия.

Для каждого конца балки можно указать два граничных условия. Все возможные виды закреплений балки, так же как и стержни, представлены на рисунке 4.

– Свободный конец стержня (рисунок 3а). Нулю равны поперечная сила и изгибающий момент . Поэтому граничные условия имеют вид:

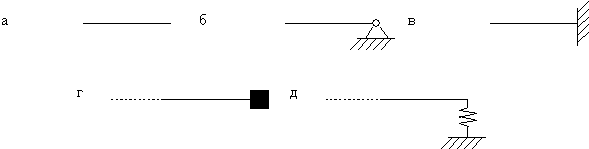
Рисунок 3 – Виды закреплении конца балки

– Шарнирно – опертый конец балки (рисунок 3б). Нулю равны прогиб и изгибающий момент . Следовательно, граничные условия таковы:

.

(1.20)

– Защемленный конец (рисунок 3в). Нулю раны прогиб и угол поворота . Граничные условия:

.

(1.21)

– На конце стержня имеется точечный груз массы (рисунок 3г). Его сила инерции может быть при помощи уравнения (1.12) записана так:

.

(1.22)

В первом условии знак плюс принимается в случае, когда точечный груз связан с левым концом стержня, и знак минус, когда он связан с правым концом стержня. Второе условие вытекает из-за отсутствия изгибающего момента.

– Упруго – опертый конец стержня (рисунок 3д). Здесь изгибающий момент равен нулю, а поперечная сила равна реакции опоры ( – коэффициент жесткости опоры). Граничные условия:

; .

(1.23)

(знак минус принимается в случае, когда упругая опора является левой, и знак плюс, когда она является правой).