Достаточное условие условного экстремума.
Пусть в точке выполнено необходимое условие условного экстремума,
,
где
– функция Лагранжа.
Потребуем
дополнительно, чтобы функции
,
,
где
,
в некоторой окрестности точки
имели непрерывные частные производные
второго порядка.
Рассмотрим приращение функции Лагранжа на множестве точек, удовлетворяющих уравнению связи:
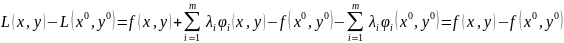
То есть приращение в целевой функции f совпадает с приращением функции Лагранжа, и это означает, что экстремумы функции и совпадают.
Это в свою очередь означает, что достаточные условия условного экстремума функции можно искать в виде достаточных условий экстремума для функции .
Например,
в качестве такого достаточного условия
можно взять условие знака определенности
квадратичной формы
при выполнении уравнения связи.
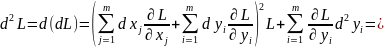
В силу подбора
множителей
мы имеем
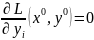
Это означает:
несмотря на то, что переменные
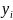зависит от переменных
,
в точке условного экстремума
второй дифференциал функции Лагранжа
можно формально вычислить так, как если
бы все переменные были независимы.
На самом
деле зависимость переменных
от переменных
учитывается при выражении
дифференциалов
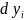через дифференциалы
.
Связь между ними получается, если продифференцировать все уравнения связи
В самом начале мы предположили, что
