25. Параметры эвольвентного зацепления. Коэффициент скольжения.
Эвольвентное зацепление позволяет передавать движение с постоянным передаточным отношением. Эвольвентное зацепление — зубчатое зацепление, в котором профили зубьев очерчены по эвольвенте окружности.
Для этого необходимо чтобы зубья зубчатых колёс были очерчены по кривой, у которой общая нормаль, проведённая через точку касания профилей зубьев, всегда проходит через одну и ту же точку на линии, соединяющей центры зубчатых колёс, называемую полюсом зацепления.
Эвольвента обладает следующими свойствами, которые используются в теории зацепления:
1) форма эвольвенты определяется радиусом основной окружности;
2) нормаль к эвольвенте в любой ее точке является касательной к основной окружности. Точка касания нормали с основной окружностью является центром кривизны эвольвенты в рассматриваемой точке;
3) эвольвенты одной и той же основной окружности являются эквидистантными (равноотстоящими друг от друга) кривыми.
Коэффициент скольжения учитывает влияние геометрических и кинематических факторов на величину проскальзывания профилей в процессе зацепления. Наличие скольжения при одновременном нажатии одного профиля на другой приводит к износу профилей. Коэффициенты скольжения выражаются формулами:
;
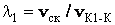где vск –– скорость скольжения; vK1-K, vK2-K –– скорости перемещения точек контакта по профилям зубьев первого и второго колеса.
За время одного оборота колеса с меньшим числом зубьев z1 второе колесо не завершает полный оборот. Следовательно, его зубья в u12 раз реже вступают в контакт, чем зубья первого колеса, и поэтому меньше изнашиваются. Для того, чтобы сравнивать интенсивность износа зубьев по коэффициентам скольжения, разделим l2 на u12 = w1/w2 = z2/z1:
l1 = vск/vK1-K; l2 = vск/vK2-K.
Расчетные формулы для l1 l2 имеют такой вид: Взаимное положение точки и плоскости
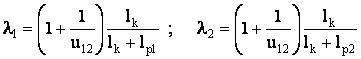
где lk –– величина алгебраическая, выражающая расстояние от полюса зацепления Р до текущего положения точки К контакта пары зубьев
lp1 и lp2 –– абсолютные значения длин отрезков РN1 и РN2.
26. Параметры эвольвентного зацепления. Коэффициент удельного давления.
Эвольвентное зацепление позволяет передавать движение с постоянным передаточным отношением. Эвольвентное зацепление — зубчатое зацепление, в котором профили зубьев очерчены по эвольвенте окружности.
Для этого необходимо чтобы зубья зубчатых колёс были очерчены по кривой, у которой общая нормаль, проведённая через точку касания профилей зубьев, всегда проходит через одну и ту же точку на линии, соединяющей центры зубчатых колёс, называемую полюсом зацепления.
Эвольвента обладает следующими свойствами, которые используются в теории зацепления:
1) форма эвольвенты определяется радиусом основной окружности;
2) нормаль к эвольвенте в любой ее точке является касательной к основной окружности. Точка касания нормали с основной окружностью является центром кривизны эвольвенты в рассматриваемой точке;
3) эвольвенты одной и той же основной окружности являются эквидистантными (равноотстоящими друг от друга) кривыми.
Коэффициент удельного давления учитывает влияние ге5ометрии зубьев (радиусов кривизны их профилей) на величину контактных напряжений, возникающих в местах соприкосновения зубьев. При чрезмерном нагружении контактные напряжения могут быть очень значительные, что приводит к выкрашиванию на рабочей поверхности зубьев.
Контактные напряжения определяются по формуле Герца
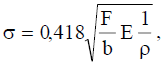
(7.23)
где F — сила взаимодействия зубьев; b — ширина зубчатых колес; Е — приведенный модуль упругости материала колес; р — приведенный радиус кривизны эвольвентных профилей в точке контакта.
Для текущего момента зацепления зубьев радиус кривизны будет равен
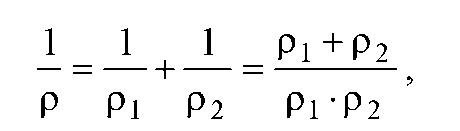
(7.24)
или, согласно свойствам эвольвентных профилей
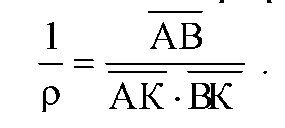
(7.25)
Коэффициентом удельного давления ϑ называется отношение
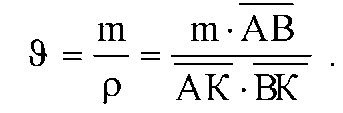
(7.26)
Коэффициент удельного давления безразмерная величина, не зависящая от модуля m, так как радиус кривизны р пропорционален модулю.
Подставим полученное выражение коэффициента удельного давления в формулу Герца (7.23) и получим
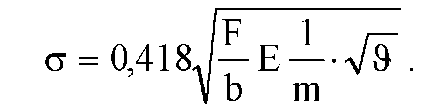
(7.27)
Анализ полученной формулы показывает, что коэффициент удельного давления возрастает при приближении к точкам А и В линии зацепления. Для уменьшения контактных напряжений необходимо, чтобы крайние точки линии зацепления не находились вблизи точек А и В.