15.Аналитическое определение кинематических характеристик.

Для аналитического определения пути, скорости и ускорения рабочего органа остановим кривошип, движущийся из точки 1 по часовой стрелке в произвольной точке В, рис. 7.3.

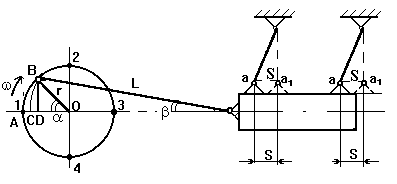
Рис. 7.3. Схема для определения кинематических характеристик колеблющегося рабочего органа при кривошипно-шатунном приводе.

Путь, пройденный ситом S из точки а в точку а1 выразим через угол поворота кривошипа a и его длину r.

Для современных сепараторов r/L £ 0,02, тогда ряд Тейлора преобразуется в следующую цифровую цепочку.

Следовательно, с достаточной точностью можно записать сито движется по гармоническому закону.

Из выражения следует, что дифференцируя по t получим выражение для определения скорости сита, υа в любой момент времени.

Ускорение сита, а можно найти, взяв вторую производную из выражения.

Для сообщения кузову колебательного движения необходима мощность, которую можно найти, пренебрегая массой шатуна (поскольку она в десятки раз меньше массы кузова).

На рис. 7.4. представлены диаграммы изменения пути S, скорости uа, ускорения а, силы инерции Ри и мощности N колеблющегося рабочего органа.

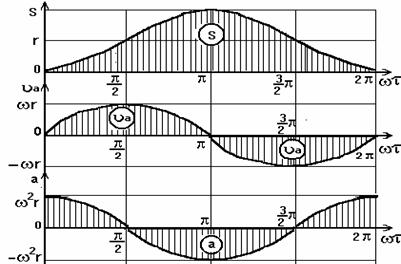
Рис. 7.4. Диаграммы изменения кинематических параметров колеблющегося органа

К полученным результатам следует сделать 2 замечания:

1) в условиях применения кривошипно-шатунного привода амплитуда колебаний не зависит от частоты колебаний и жесткости подвесок;

2) при теоретических исследованиях сделаны следующие допущения:

L>>r;

дуга а-а1 - прямая;

система абсолютно жесткая.

16.Задачи геометрического анализа механизмов.

Задачи геометрического анализа

Целью геометрического анализа является определение функций положения ме-

ханизма - зависимостей выходных координат x1, x2 ,..., xm , характеризующих положе-

ния его звеньев, от заданных входных координат q1, q2 ,..., qn . Для механизмов с n

степенями подвижности эти функции записываются в форме

xs = Πs (q1, q2 ,..., qn ) , s =1,2,...,m. (1)

Определение этих зависимостей составляет прямую задачу геометрического

анализа. При заданных законах изменения входных координат qk (t) (k =1,2,...,n) мож-

но, решив прямую задачу, найти законы изменения выходных координат, как функций

времени

xs (t) = Πs [q1(t), q2 (t),..., qn (t)], s =1,2,...,m. (2)

Для механизма с одной степенью подвижности функции положения являются

функциями одной независимой переменной q :

xs = Πs (q) , s =1,2,...,m. (3)

Исследование функций положения механизма, также проводимое в ходе геомет-

рического анализа, позволяет оценить его функциональные возможности.

В механизмах с несколькими степенями подвижности приходится решать об-

ратную задачу геометрического анализа, связанную с определением входных коорди-

нат q1, q2 ,..., qn по заданным значениям некоторых выходных координат x1, x2 ,..., xm .

В общем случае речь идет об определении функций

qk = Φk (x1, x2 ,..., xm ) , k =1,2,..., n . (4)

17.Задачи кинематического синтеза механизмов, ограничения.

Часто ставится обратная задача по кинематической схеме необходимой определить размеры звеньев.

При некоторые механизмы должны удовлетворять условия связывающих научным механизмом, технологическими и эксплуатационными методами.

Эти условия деляться на основные и дополнительные.

Основные условия записываются в виде функции независимыми параметрами назывывается целевой функцией.

Все остальные условия относятся к дополнительным и записываются в виде математической форме в виде ограничений.

1-ое ограничение

Ограничение на длины звеньев L1,L2,L3,…. в математической форме записывается неравенство L0<L1<L2

2-ое ограничение

Кривошипнокаромыслового механизма должно выполняться условие существующего кривошипа который является наименьшим звеном L1+L4<L2+L3

3-ое ограничение

Угол давления в кинематической паре образован шатуном и выходным звеном не должно быть больше допустимого значения Vi<=Vдоп

Угол давления- это угол между вектором скорости и вектором силы.

4-ое ограничение

Ограничение на массу и моменты инерции звеньев