13.Графическое интегрирование, методы, применение.

Применяется два метода графического интегрирования – метод площадей и метод хорд.

Графическое интегрирование методом площадей

Этот метод основан на геометрической интерпретации (физическом смысле) интеграла. Рассмотрим данный метод на примере интегрирования диаграммы скоростей. В результате интегрирования необходимо построить диаграмму перемещений.

где А – площадь под кривой скорости на выделенном участке (что соответствует физическому смыслу интеграла).

Для интегрирования методом площадей выделяют на оси абсцисс N положений (в пределах одного цикла). Определяют площадь А1 (в мм2) под графиком скорости на участке 0-1, площадь А2 – на участке 1-2, площадь А3 – на участке 2-3 и т.д.

Умножив эти площади на масштаб скоростей и масштаб времени диаграммы скоростей, получают истинные перемещения на выделенных участках, по которым определяют общие перемещения в каждом положении исследуемого звена в расчете от нулевого положения:

S0-1 = Kv * Kt * A1; S1-2 = Kv * Kt * A2; S2-3 = Kv * Kt * A3; и т.д.

S1= S0-1; S2= S1 + S1-2; S3= S2 + S2-3; и т.д.

После определения всех перемещений задают масштаб Ks, в котором строят диаграмму перемещений.

Графическое интегрирование методом хорд

Данный метод основан на том, что интегрирование есть процесс обратный дифференцированию. Поэтому при этом методе производятся все те же действия, что и при дифференцировании методом хорд, только в обратном порядке:

- делят интегрируемую кривую на ряд участков;

- находят среднее значение функции на каждом участке (приближенно можно принимать за среднее значение функции посередине данного участка);

- сносят эти средние значения на ось ординат интегрируемой диаграммы;

- слева от начала координат на оси абсцисс отмечают полюс Р на некотором полюсном расстоянии H;

- соединяют полюс Р с отмеченными на оси ординат точками, характеризующими средние значения интегрируемой функции на выделенных участках. Полученные лучи характеризуют направления хорд на соответствующих участках искомой функции;

- из начала координат проводят хорду на первом участке, параллельную первому лучу; из конца первой хорды на втором участке проводят хорду, параллельную второму лучу и т.д.

В результате, после построения всех хорд, формируется ломаная кривая, по вершинам которой надо провести плавную кривую. При интегрировании диаграммы скоростей полученная кривая будет представлять собой диаграмму перемещений (соответственно, при интегрировании диаграммы ускорений, получается диаграмма скоростей). Масштабы полученных диаграмм определяются из зависимостей, выведенных для графического дифференцирования:

Ks = Kv * Kt * H

Kv = Ka * Kt * H1

14.Определение передаточных функций.

Передаточная функция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи и цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.

В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях.

Линейные стационарные системы

Пусть u(t) — входной сигнал линейной стационарной системы, а y(t) — её выходной сигнал. Тогда передаточная функция W(s) такой системы записывается в виде:

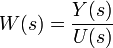
где U(s) и Y(s) — преобразования Лапласа для сигналов u(t) и y(t) соответственно:

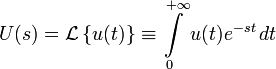
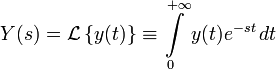
Дискретная передаточная функция

Для дискретных и дискретно-непрерывных систем вводится понятие дискретной передаточной функции. Пусть u(k) — входной дискретный сигнал такой системы, а y(k) — её дискретный выходной сигнал, k=0,1,2…. Тогда передаточная функция W(z) такой системы записывается в виде:

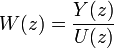
где U(z) и Y(z)— z-преобразования для сигналов u(k) и y(k) соответственно:

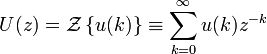
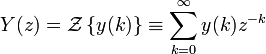
Свойства передаточной функции

1. Для стационарных объектов с сосредоточенными параметрами передаточная функция — это дробно-рациональная функция комплексной переменной (s):

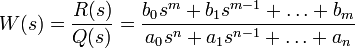
2. Знаменатель передаточной функции — это характеристический полином системы. Полюсы передаточной функции — это корни соответствующего характеристического полинома.

3. В физически реализуемых системах порядок числителя передаточной функции m не может превышать порядка её знаменателя n.

4. Импульсная переходная функция представляет собой оригинал (преобразования Лапласа) для передаточной функции.