36.Задачи силового расчёта, теоретические предпосылки.

Силовой расчёт включает в себя определение реакций в кинематических парах и внешних уравновешенной силой(момента).

В тихоходной механике где ускорения не велики силой инерции можно принебреч.

37.Аналитический метод силового расчёта.

Аналитические методы, позволяют проводить анализ нелинейной цепи в общем виде, а не для частных значений параметров элементов схемы. В этом заключается их главное преимущество. Однако аппроксимация нелинейной характеристики, лежащая в основе данных методов, изначально обусловливает внесение в расчеты большей или меньшей погрешности. Как и при графическом анализе цепей, при применении аналитических методов используются характеристики нелинейных элементов для мгновенных значений, по первым гармоникам и для действующих значений. При этом для расчета цепей переменного тока наиболее широкое распространение получили следующие аналитические методы:

-метод аналитической аппроксимации;

-метод кусочно-линейной аппроксимации;

-метод гармонического баланса;

-метод эквивалентных синусоид (метод расчета по действующим значениям).

В первых трех случаях обычно используются характеристики нелинейных элементов для мгновенных значений. Характеристики нелинейных элементов по первым гармоникам используются при применении частного варианта метода гармонического баланса - метода расчета по первым гармоникам. В свою очередь, метод эквивалентных синусоид основан на применении характеристик нелинейных элементов для действующих значений.

38.Графический метод силового расчёта.

Графические методы расчета позволяют проводить анализ нелинейных цепей переменного тока для частных значений параметров с использованием характеристик нелинейных элементов для мгновенных значений, по первым гармоникам и действующим значениям.

39.Определение уравновешивающей силы.

В тех случаях, когда требуется найти только неизвестную внешнюю силу без определения реакций в кинематических парах (например, уравновешивающую силу или момент), удобно воспользоваться методом Жуковского Н.Е., не прибегая к последовательному силовому расчету всего механизма.

Метод основан на принципе возможных перемещений – если система находится в равновесии, то сумма работ внешних сил и моментов на малых возможных перемещениях равна нулю ( ∑ Ai = 0). Так как с помощью сил инерции (по принципу Даламбера) механизм приведен в состояние равновесия, то в данном случае принцип возможных перемещений применим.

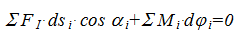
Перейдем к конкретному мгновенному положению механизма, разделив все члены на бесконечно малый промежуток времени (dt), за который происходят указанные малые перемещения:

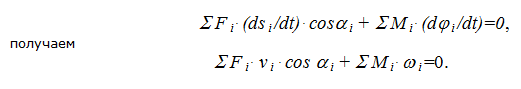
Таким образом, уравнение работ трансформируется в уравнение мгновенных мощностей и принцип возможных перемещений в применении к механизму можно сформулировать следующим образом – если механизм находится в равновесии, то сумма мгновенных мощностей всех внешних сил и моментов, приложенных к звеньям механизма, равна нулю.

Жуковским Н.Е. был предложен метод составления этого уравнения с использованием плана скоростей (рисунок 19).

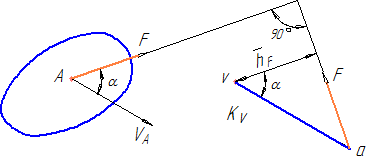
Рисунок 19

На рисунке 19 изображено некоторое звено, в точке А которого приложена сила F. Скорость VA этой точки изображается на плане скоростей вектором va в масштабе KV. Перенесем силу F в точку "а" плана скоростей, повернув на 900 (в любую сторону). Возьмем формально момент этой повернутой силы относительно полюса плана скоростей:

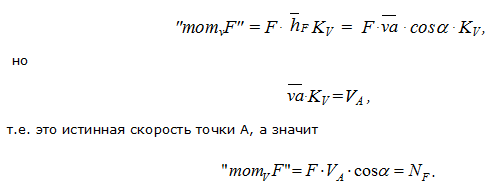
В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.

Таким образом для составления уравнения Жуковского прикладывают все силы, действующие на звенья механизма (включая силы инерции), в соответствующие точки плана скоростей, предварительно повернув их на 900. Взяв формально сумму моментов этих повернутых сил относительно полюса плана скоростей, фактически получают уравнение развиваемых ими мощностей.

К полученному уравнению добавляют мощности, развиваемые моментами (включая моменты сил инерции).

В уравнение Жуковского мощности должны входить с соответствующими знаками (см. рисунок 16 ). В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.

Примечание: для составления уравнения Жуковского можно на повернутый (на 900) план скоростей прикладывать силы в своем истинном направлении.