Основы реляционной алгебры

Реляционная алгебра состоит из двух групп по четыре оператора.

1. Традиционные операции над множествами: объединение, пересечение, разность и декартово произведение.

2. Специальные реляционные операции: выборка, проекция, со­единение, деление.

Операции над множествами.

Объединение возвращает отношение, содержащее все кортежи, которые принадлежат либо одному из двух заданных отношений, либо им обоим .

R1

FIO	Year	Job	Chair
Цветкова С.С.	1960	Доцент	23
Козлов К. К.	1959	Доцент	23
Петров П. П.	1960	Ст. преп.	24
Лютикова Л.Л.	1977	Ассистент	24
R2
FIO	Year	Job	Chair
Иванов И. И.	1948	Зав каф.	22
Сидоров С. С.	1953	Проф.	22
Гиацинтова Г. Г	1945	Проф.	22
Цветкова С. С.	1960	Доцент	23
Козлов К. К.	1959	Доцент	23

ОБЪЕДИНЕНИЕ

FIO	Year	Job	Chair
Иванов И. И.	1948	Зав каф.	22
Сидоров С. С.	1953	Проф.	22
Гиацинтова Г. Г	1945	Проф.	22
Цветкова С. С.	1960	Доцент	23
Козлов К. К.	1959	Доцент	23
Петров П. П.	1960	Ст. преп.	24
Лютикова Л.Л.	1977	Ассистент	24

Пересечение возвращает отношение, содержащее все кортежи, которые принадлежат одновременно двум заданным отношениям.

ПЕРЕСЕЧЕНИЕ

FIO	Year	Job	Chair
Цветкова С. С.	1960	Доцент	23
Козлов К. К.	1959	Доцент	23

Разность возвращает отношение, содержащее все кортежи, ко­торые принадлежат первому из двух заданных отношений и не при­надлежат второму.

РАЗНОСТЬ

FIO	Year	Job	Chair
Иванов И. И.	1948	Зав каф.	22
Сидоров С. С.	1953	Проф.	22
Гиацинтова Г. Г	1945	Проф.	22

Job

Зав каф.

Проф.

Ст. преп.

Доцент

Ассистент

Произведение возвращает отношение, содержащее все возмож­ные кортежи, которые являются сочетанием двух кортежей, принад­лежащих соответственно двум заданным отношениям.

Chair

22

23

R3 R4

ПРОИЗВЕДЕНИЕ

Job	Chair
Зав каф.	22
Зав каф.	23
Проф.	22
Проф.	23
Ст. преп.	22
Ст. преп.	23
Доцент	22
Доцент	23
Ассистент	22
Ассистент	23

ПРИМЕР.

Исходными являются три отношения R1 R2 и R3. Все они имеют эквивалентные схемы.

• R₁= (ФИО, Паспорт, Школа);

• R₂= (ФИО, Паспорт, Школа);

• R₃= (ФИО, Паспорт, Школа).

Рассмотрим ситуацию поступления в высшие учебные заведения когда разрешены репетиционные вступительные экзамены, которые сдаются раньше основных вступительных экзаменов в вуз. Отношение R1 содержит список абитуриентов, сдававших репетиционные экзамены. Отношение, R2 содержит список абитуриентов, сдававших экзамены на общих условиях. Отношение R3 содержит список абитуриентов, принятых в институт. Будем считать, что при неудачной сдаче репетиционных экзаменов абитуриент мог делать вторую попытку и сдавать экзамены в общем потоке, поэтому некоторые абитуриенты могут присутствовать как в первом, так и во втором отношении.

Ответим на следующие вопросы:

1. Список абитуриентов, которые поступали два раза и не поступили в вуз. R = R₁ R₂ \ R₃

2. Список абитуриентов, которые поступили в вуз с первого раза. R = (R₁ \ R₂ R₃) 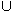(R₂ \ R₁ R₃)

3. Список абитуриентов, которые поступили в вуз только со второго раза.

Прежде всего это те абитуриенты, которые присутствуют в отношениях R₁ и R₂, потому что они поступали два раза, и присутствуют в отношении R₃, потому что они поступили. R = R₁ R₂ R₃

4. Список абитуриентов, которые поступали только один раз и не поступили.

Это прежде всего те абитуриенты; которые присутствуют в R₁ и не присутствуют в R₂, и те, кто присутствуют в R₂ и не присутствуют в R₁. И разумеется, никто из них не присутствует в R₃. R = (R₁ \ R₂) (R₂ \ R₁) \ R₃