П ринимая во внимание, что

Окончательно получим

M= pm₂w₂k_об2Ф_mI₂cosψ₂=C_MФ_mI₂cosψ₂, (49)

где C_M= pw₂k_об2 - постоянный коэффициент.

Таким образом, при неизменных токе I₂ и магнитном поле величина результирующего электромагнитного момента M тем меньше, чем больше угол ψ₂. При ψ₂=π/2 момент M=0, так как на половину проводников действует усилие, направленное в од­ну сторону, а на другую половину - такое же усилие, направленное в другую сторону. Формула (49) позволяет связать величину момен­та с физическими явлениями, происходящими в двигателе, и ею удоб­но пользоваться для качественного анализа поведения асинхронной машины в различных режимах.

2.2. Определение вращающего момента по мощности, передаваемой через магнитное поле ротору

В предыдущем параграфе получено выражение для электромагнит­ного момента М в виде (49)

M=C_MФ_mI₂cosψ₂,

Одним из недостатков этой формулы является то, что при изменении нагрузки одновременно меняются все три величины (Ф_m, I₂, cosψ₂), поэтому выражение неудобно для анализа зависимости элек­тромагнитного момента от скольжения. Для этих целой может быть получено на основе энергетической диаграммы рис.1 и Г-образной схемы замещения асинхронной машины рис.5 другое, более удобное выражение.

Электромагнитная мощность, передаваемая из статора в ротор посредством магнитного поля, эквивалентна активной мощности, вы­деляемой в активном сопротивлении схемы замещения r ^/₂/S

P_ЭМ = ω₁M = m₁I ^/2₂ r ^/₂ / S = m₂I ²₂r₂ / S.

Часть этой мощности выделяется в виде электрических потерь в об­мотке ротора и нагревает ее

ΔP_ЭЛ2 = m₁I ^/2₂ r ^/₂ = m₂I ²₂ r₂.

Оставшаяся часть представляет собой полную механическую мощность Р_МЕХ, которая выделяется в активном сопротивлении схемы замеще­ния r₂’(1-S)/S, (28)

P_МЕХ = P_ЭМ-ΔР_ЭЛ2 = m₁ I ^/2₂ r ^/₂ / S - m₁I ^/2₂ r ^/₂ = m₁ I ^/2₂ r ^/₂(1-S)/S= ωM

И з полученного выражения для полной механической мощности найдем электромагнитный момент

(50)

Т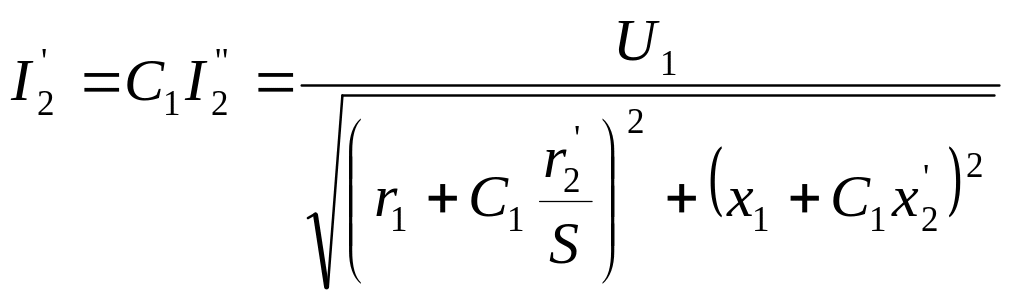 ок I ^/₂ является функцией скольжения S, поэтому чтобы найти зависимость M=f(S), нужно выразить величину тока I ^/₂ через параметры схемы замещения. Заменив комплексный коэффициент С₁ его действительной частью, из Г-образной схемы замещения найдем действующее значение тока I ^/₂ (38), (42), (43)

(51)

или для упрощенной Г-образной схемы замещения при Ċ₁≈1 полу­чим выражение для тока ротора в виде

(52)

Из формулы (52) следует, что при увеличении скольжения S ток I ^/₂ будет возрастать рис.7 и в пределе при S=∞ дости­гнет значения I ^/_2пред.

Ток в обмотке статора I₁ также является функцией скольже­ния S и для упрощенной Г-образной схемы замещения при С₁≈1 равен (44)

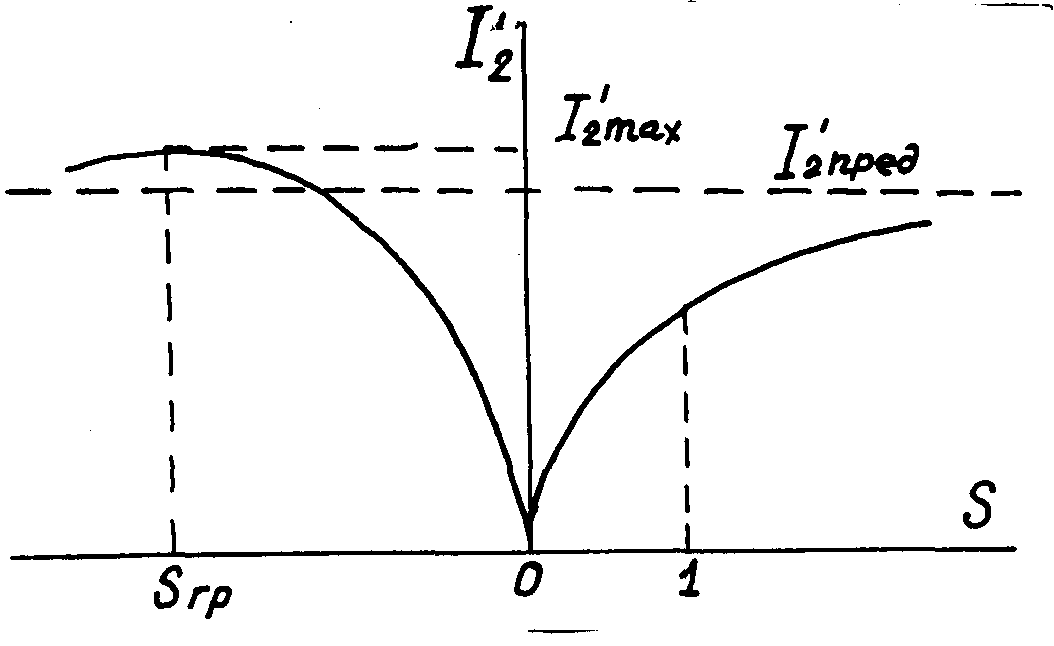
Рис.7. Зависимость тока ротора от скольжения

(53)

Для схемы замещения ротора рис.2 найдем выражение cosψ₂=f(S) и построим график рис.8

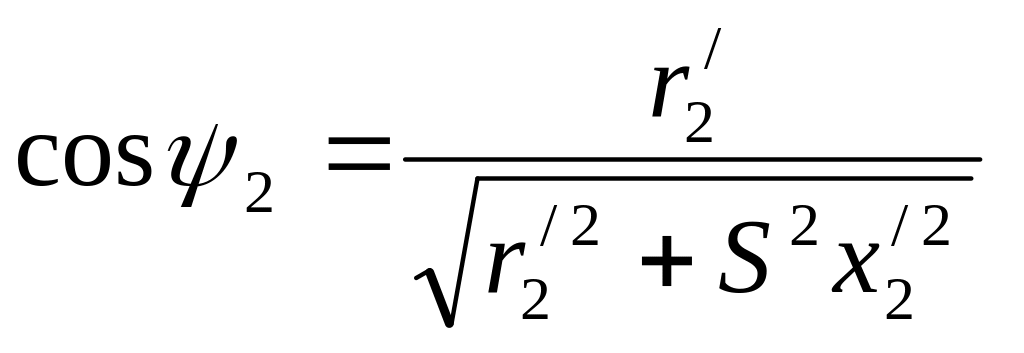( 54)

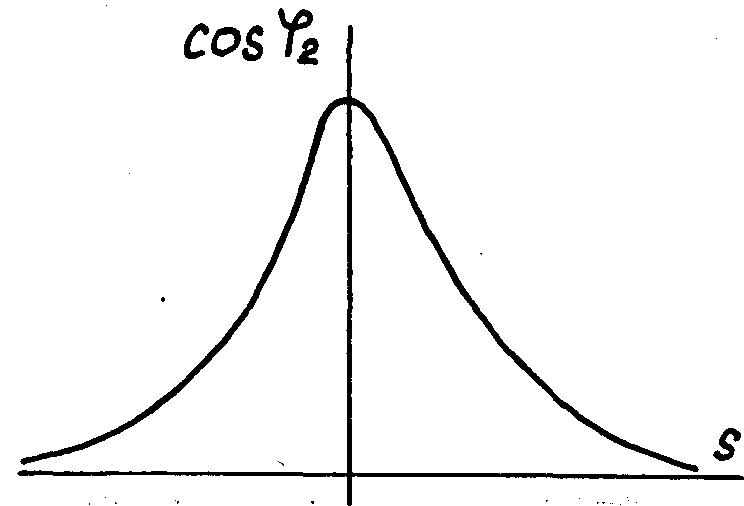
Рис.8. Зависимость коэффициента мощности обмотки ротора от скольжения S.

П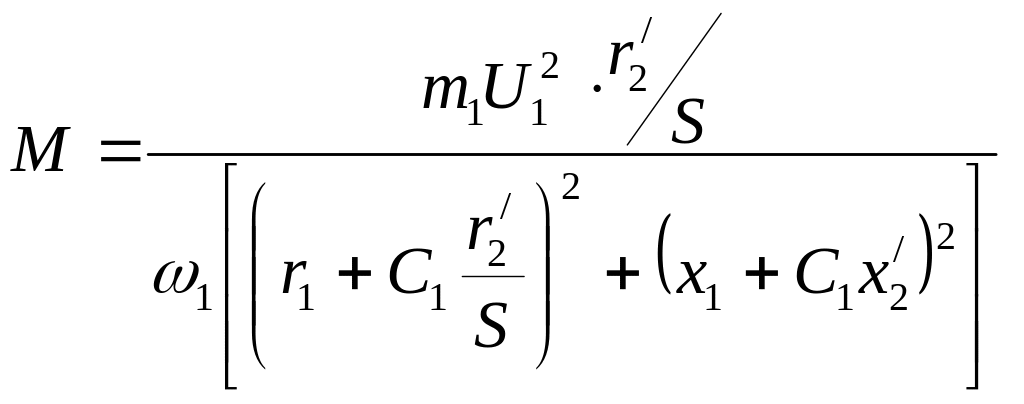 одставив значения тока I ^/₂ в выражение для электромагнитного момента (50), получим

(55)

К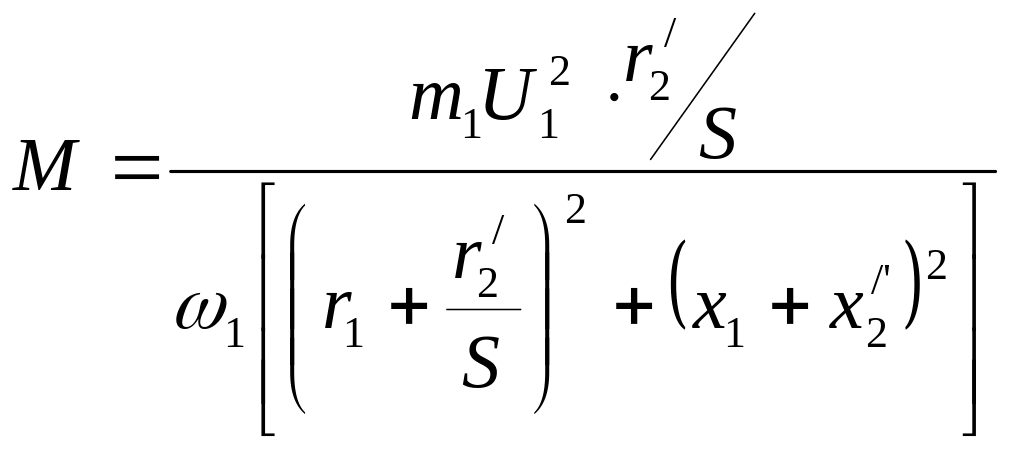 ак уже отмечалось, для асинхронных машин мощностью более 8-10 кВт можно принять С₁≈1, тогда формула для электромагнитного момента упростится и примет вид

(56)

Зависимость M=f(S) или S=f(M) рис.9 называется механической характеристикой асинхронной машины.