3.4. Включение добавочных сопротивлений в цепь ротора

Конструктивные особенности асинхронной машины с фазным ротором позволяют в каждую фазу обмотки ротора включить добавочные сопротивления - активные или реактивные. Введение добавочных со­противлений в цепь ротора дает возможность ограничить величину пускового тока, увеличить до значения максимального пусковой момент, осуществить плавный запуск двигателя и т.д.

3.4.1. Добавочные активные сопротивления в цепи ротора

Увеличение добавочных активных сопротивлений в цепи ротора вызывает увеличение критического скольжения

(67)

Пусковой момент двигателя при увеличении r’_доб2 вначале возра­стает до максимального значения, равного критическому при S_K=1, а затем, при дальнейшем увеличении r’_доб2 происходит уменьшение пускового момента. Изменения добавочного сопротивления r’_доб2 не оказывают влияния на величину критического момента рис.14

Таким образом КПД двигателя мало изменяется при изменении частоты.

На ряс.12 представлено семейство механических характеристик асинхронной машины при изменении частоты источника питания. Ис­следование характеристик показывает, что увеличение частоты, с одной стороны, приводит к пропорциональному увеличению скорости, что может быть использовано в регулируемых электроприводах, но с другой стороны, приводит к значительному уменьшению критического момента т.е. перегузочной способности. Поэтому на практике исполь­зуют одновременное изменение и частоты и напряжения источника пи­тания, например, по закону U₁ / f=const.

3.3. Включение добавочных сопротивлений в цепь статора

П усковой ток асинхронного двигателя с короткозамкнутым ротором в 5-7 раз превышает номинальное значение тока. Если питаю­щая сеть недостаточно мощная, а асинхронный двигатель имеет боль­шую мощность, то необходимо ограничить величину пускового тока, чтобы исключить понижение напряжения в сети ниже допустимого значения. Один из способов ограничения пускового тока асинхронного двигателя с короткозамкнутым ротором - введение в цепь ста­тора симметричного активного или реактивного добавочного сопро­тивления Z_доб [6].

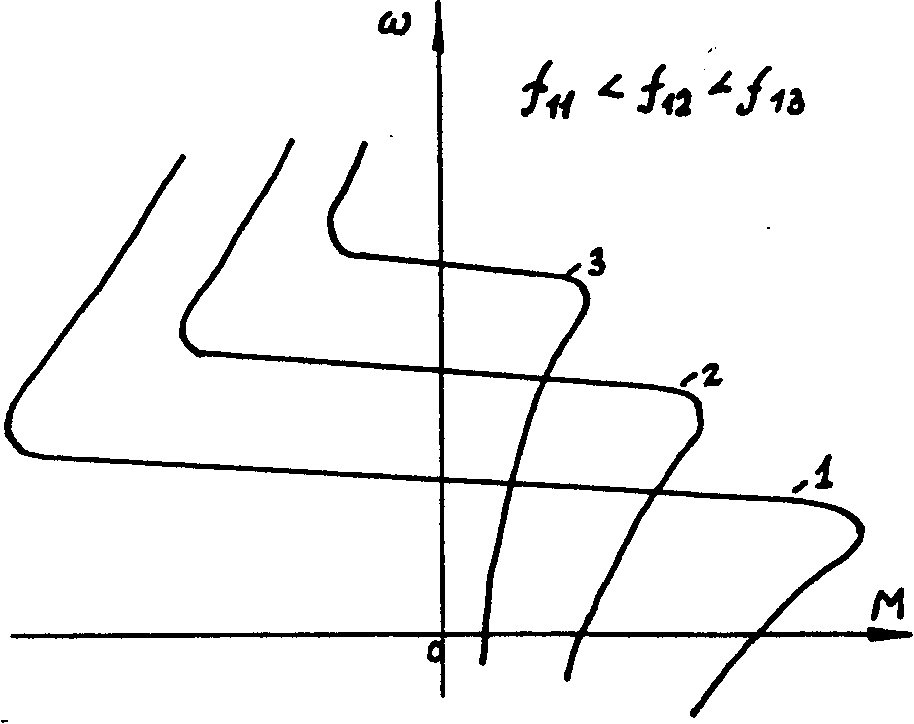
f₁₁<f₁₂<f₁₃ Рис.12. Механические характеристики асинхронной машины при изменении частоты источника питания.

Падение напряжения на добавочном сопротивлении в цепи статора является функцией тока. Таким образом, по мере уменьшения пускового тока напряжение, приложенное к обмоткам двигателя. растет. На рис.13 показаны естественная и искусственные характе­ристики асинхронного двигателя с короткозамкнутым ротором при включении в цепь статора активного сопротивления r_доб, индук­тивного сопротивления x_доб и при снижении напряжения источни­ка питания U₁. Следует обратить внимание, что если подобрать параметры r_доб, x_доб и U так, чтобы обеспечивались одинаковые пусковые моменты, то при включении в цепь статора x_доб получаются более высокие моменты, чем при включении r_доб. При снижении напряжения получаются меньшие моменты двигателя по сравнению со способом ограничения пусковых тока и момента, когда вводятся добавочные сопротивления. Пуск в ход двигателя при r_доб позволяет получить более высокий cosφ, чем при x_доб, но зато при x_доб меньше потери.

Величина сопротивления, включаемого в цепь статора, опреде­ляется, исходя из допустимого значения тока статора [5].

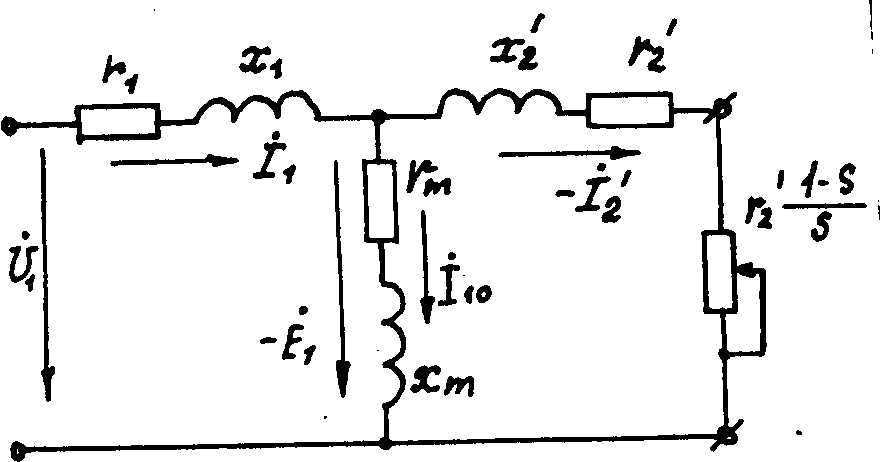
Рис.3. Т-образная схема замещения асинхронной машины.

Как и в трансформаторе при приведении параметров асинхрон­ной машины исходят из энергетического соответствия замещенной и реальной машин, но в асинхронной машине приведение параметров ро­тора к цепи статора несколько сложнее, чем в трансформаторе из-за пространственного распределения обмоток вдоль окружностей ротора и статора.

Так, из выражений (18) и (19) следует, что коэффициент при­ведения токов равен

Приведенная ЭДС Е ^/₂ обмотки ротора должна быть равна ЭДС Е₁ об­мотки статора, тогда, используя выражения (11) и (12), получим

, (29)

где - коэффициент приведения ЭДС. (30)

При приведении сопротивления r₂ исходят из того, что по­тери в активном сопротивлении ротора должны остаться без измене­ния. Тогда получим

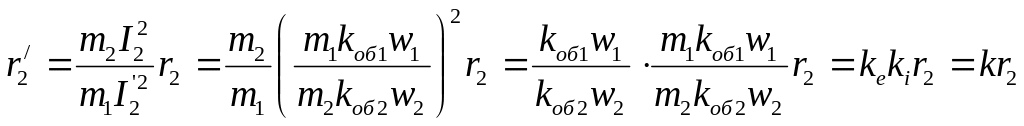, (31)

где k=k_e · k_i - коэффициент приведения сопротивлений.

При приведении индуктивного сопротивления рассеяния исходят из того, что угол ψ₂ между ЭДC E₂ и током I₂ остается неизменным

tgψ₂=x₂/r₂=x₂’/r₂’,

тогда x₂’=r₂’x₂/r₂=kx₂. (32)

При определении коэффициентов приведений для короткозамкнутой обмотки асинхронной машины принимают w₂=0,5; m₂=z₂; k_об2=1, тогда k_e=2w₁k_об1; k_i=2m₁k_об1/z₂; и k=4m₁(w₁k_об1)²/z₂.

Для Т-образной схемы замещения асинхронной машины запишем уравнения напряжений и токов в виде

U ₁= - Ė₁+Zİ₁ = - Ė₁ + r₁İ₁ + jx₁İ₁

Ė ^/₂ = Ė₁ = Z ^/_2Sİ ^/₂ =( r ^/₂ / S) İ ^/₂ + jx ^/₂İ ^/₂ (33)

İ₁ = İ₁₀ + (-İ ^/₂)

где Z ^/_2S=Z ^/₂+r ^/₂(1-S)/S=r ^/₂ + jx ^/₂ + r ^/₂ (1-S)/S = r ^/₂/S + jx ^/₂.

По своей структуре эта система уравнений аналогична системе ура­внений для трансформатора, ко вторичной обмотке которого подклю­чено сопротивление нагрузки r_МЕХ=r₂’(1-S)/S. Количественное различие между схемами замещения асинхронной машины и трансформа­тора обусловлено значительно большим током холостого ходе асинхронной машины I₁₀=(0,25-0,5)I_1НОМ. Это объясняется наличием в магнитной цепи асинхронной машины воздушного зазора δ между статором и ротором, что приводит к увеличению магнитного сопроти­вления цепи и соответствующему уменьшению электрического сопротив­ления намагничивающей ветви схемы замещения. Это утверждение хо­рошо иллюстрируется формулой, выведенной Л.Р.Нейманом

где Z_Э - полное сопротивление контура намагничивания эквивалентной схемы замещения,

Z_М - полное магнитное сопротивление.

Системе уравнений (33) соответствует пространственно-времен­ная диаграмма асинхронной машины, приведенной к трансформатору. рис.4. По своему виду эта диаграмма похожа на диаграмму трансфор­матора. но имеет несколько более сложное физическое толкование. Диаграмма асинхронной машины изображается на комплексной плоскости, во-первых, для однопериодной модели, во-вторых, имеет две системы осей: одни оси связаны со статором, а вторые связаны с заторможенным в произвольном положении ротором (как правило, оси фаз статора не совпадают с осями фаз ротора).

При переходе от комплексных величин, изображенных векторами на комплексной плоскости, которые вращаются с угловой скоростью ω₁=2πf₁ / p, к мгновенным фазным величинам нужно спроектировать векторы статорных величин на оси фаз статора (A₁; B₁; C₁), а векторы роторных величин на неподвижные произвольно ориенти­рованные оси фаз ротора (A₂; B₂; C₂).

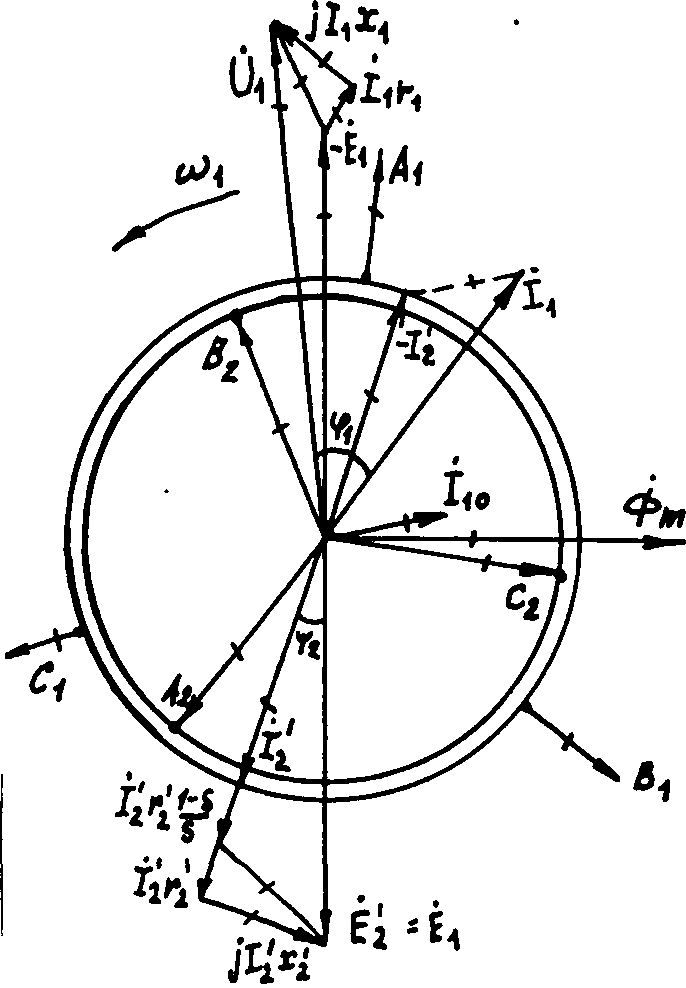
Рис.4. Пространственно-временная диаграмма асинхронной машины. P=1.

Итак, можно сделать вывод, что для исследования электромаг­нитных процессов в асинхронной машине может быть использована теория трансформаторов, что позволяет упростить задачу исследо­вания.

Т-образная схема замещения хорошо отражает реальные физиче­ские процессы, но при исследовании, например, механических характеристик асинхронной машины намного удобнее пользоваться вы­ражениями, которые содержат вместо ЭДС Е₁=E ^/₂ напряжение сети U₁. В Т-образной

Коэффициент мощности при понижении напряжения имеет тенден­цию к увеличению, особенно заметному при небольших нагрузках, так как уменьшается намагничивающий ток двигателя.

Чтобы определить, как влияет изменение напряжения на КПД двигателя, примем момент статического сопротивления М_С, созда­ваемый рабочей машиной, постоянным, не зависящим от угловой ско­рости вращения. Тогда при уменьшении напряжения механические по­тери остаются практически без изменения, потери в стали уменьша­ются приблизительно пропорционально квадрату напряжения источни­ка питания, потери в обмотке ротора увеличиваются пропорциональ­но I₂² (ΔР_Э2=m₂I₂²r₂, M_C=M=C_MI₂’Ф_m, при уменьшении магнитного потока Ф_m возрастает ток ротора I₂’ с тем, чтобы момент оставался постоянным), потери в обмотке ста­тора зависят от соотношения между токами I₁₀ и I₂, из которых ток намагничивания I₁₀ уменьшается, а ток ротора возрастает. В целом КПД асинхронного двигателя при малых нагрузках с уменьшением напряжения возрастает, а при увеличении нагрузки падает.

Приведенный выше анализ влияния изменение напряжения источ­ника питания на механические характеристики асинхронной машины выполнен без учета влияния насыщения стали и вытеснения токов в стержнях обмотки ротора короткозамкнутого асинхронного двигателя. Эти явления приводят к еще большему уменьшению значений мо­мента и тока асинхронного двигателя при уменьшении напряжения, подводимого к обмотке статора, по сравнению с теми значениями, которые определяются по формулам (52) и (56).