3.4.3. Параллельное включение реакторов и активных сопротивлений в цепь ротора

Как влияет на вид механической характеристики асинхронного двигателя параллельное включение активного сопротивления и реак­тора в цепь ротора?

В первый момент пуска асинхронного двигателя частота тока в роторе и реакторе велика. Поэтому основная часть тока ротора идет через активное сопротивление r_доб2, рис.16. Это сопротивление, в основном, и определяет величины пусковых тока и момента двигателя. По мере увеличения скорости и уменьшении часто­ты тока в роторе, индуктивное сопротивление реактора уменьшается, и через реактор начинает протекать все большая часть тока ротора. При скорости ротора близкой к номинальной частота тока в обмотке ротора примерно равна 1..2 Гц, тогда индуктивное сопротивление реактора будет незначительным, и почти весь ток будет протекать через реактор. Благодаря изменению параметров роторной цепи при пуске

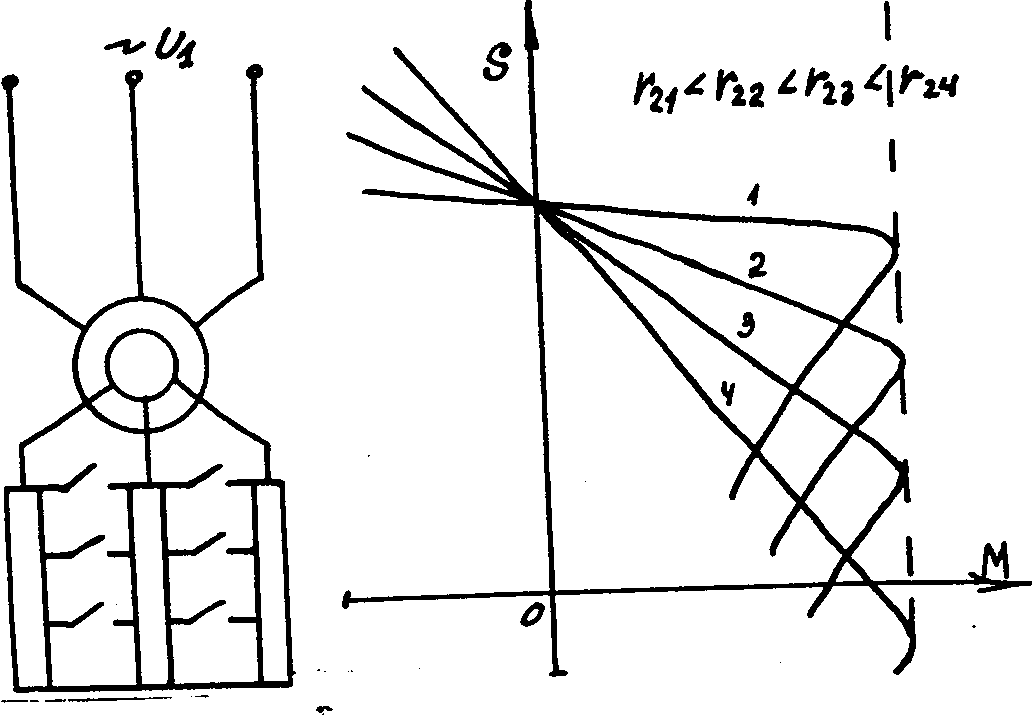
r₂₁<r₂₂<r₂₃<r₂₄ Рис.14. Механические характеристики асинхронной машины при изме­нении активного сопротивления в цепи ротора.

Расчет ступеней добавочных сопротивлений для пусковой диаграммы асинхронного двигателя осуществляется графическими или аналитическими методами [5, 6].

3.4.2. Последовательное включение реакторов и добавочных активных сопротивлений в цепь ротора

Реакторы позволяют получить плавное ускорение привода при малом количестве ступеней ускорения, играют роль автоматического регулятора тока в роторе и обеспечивают постоянство момента дви­гателя в процессе пуска.

Пусть активное пусковое сопротивление r’_доб2 и реактор с индуктивным сопротивлением x’_доб2 соединены последовательно и включены в каждую фазу обмотки ротора рис.15. В начальный момент пуска асинхронного двигателя, когда частота тока в обмотке ротора равна частоте сети, индуктивное сопротивление реактора велико и оно ограничивает величину пускового тока. По мере раз­гона двигателя ЭДС ротора E_2S=E₂S уменьшается, но

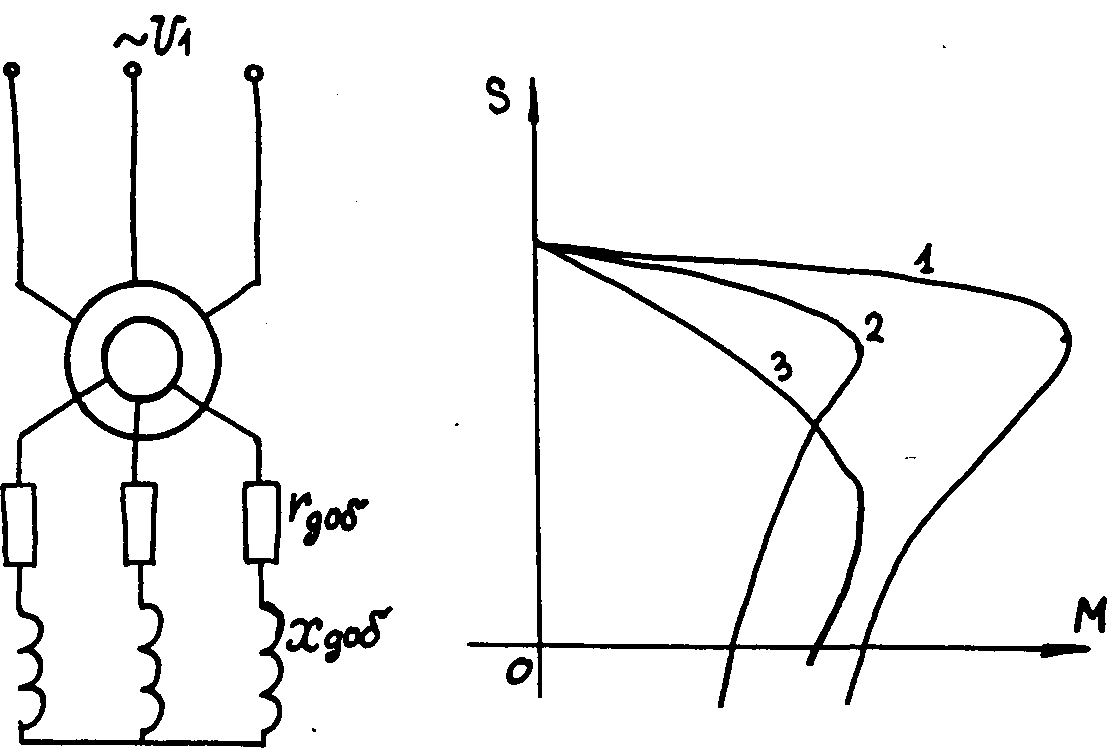
Рис.15. Механические характеристики асинхронного двигателя.

1 - естественная. 2 - при включении в цепь ротора добавочного индуктивного сопротивления. 3 -

C другой стороны, если бы удалось вращающуюся асинхронную машину заменить на эквивалентную ей по энергетическим и электро­магнитным соотношениям машиной с неподвижным ротором, то для исследования асинхронной машины можно было бы применить теорию трансформаторов.

Решение такой задачи возможно, поскольку, как было установ­лено в параграфе 1.3. при вращении ротора МДС и магнитные поля статора и ротора, вращаются с одинаковой угловой скоростью ω₁ и образуют результирующее вращающееся магнитное поле. Но одного этого условия еще недостаточно для приведения режима работы вра­щающейся асинхронной машины и эквивалентному режиму неподвижной машины. Для этого необходимо, чтобы остались неизменными величи­ны токов обмоток и их фазовые сдвиги относительно друг друга. В этом случае остаются неизменными величины результирующих МДС и магнитных потоков, а также величины потребляемой из сети мощно­сти и электромагнитной мощности, передаваемой через зазор с по­мощью магнитного поля от статора в ротор. Кроме того, при пере­ходе к неподвижной машине механическая мощность должна быть представлена равной ей электрической мощностью.

На основании второго закона Кирхгофа составим уравнения на­пряжений для фазы обмоток ротора и статора

(21)

где U₁ - фазное напряжение источника питания (сети);

I₁; I₂; r₁; r₂ – токи и активные сопротивления фаз обмо­ток статора и ротора;

Е₁; Е_2S – действующие значения ЭДС (11) и (15), наводимых основным магнитным потоком Ф;

Е_1σ; E_2σ - действующие значения ЭДС, наводимых потоками рассеяния.

ЭДС рассеяния обмоток статора и ротора можно выразить следующим образом

(22)

г де x₁; x_2S - индуктивные сопротивления рассеяния фаз ста­тора и вращающегося ротора, которые равны

, (23)

x₂ - индуктивное сопротивление рассеяния неподвижного ротора;

где L₁, L₂ - индуктивности фаз обмоток статора и ротора от потоков рассеяния Ф_1σ и Ф_2σ. Так как потоки рассеяния обмоток замыкаются, в основном, по воздуху, то будем считать индуктивности L₁ и L₂ величинами по­стоянными.

С учетом выражений для ЭДС рассеяния (22) систему уравнений напряжений (21) представим в виде

(24)

Из второго уравнения системы напряжений найдем ток фазы обмотки ротора

, (25)

Этому уравнению соответствует схема замещения вращающегося рото­ра

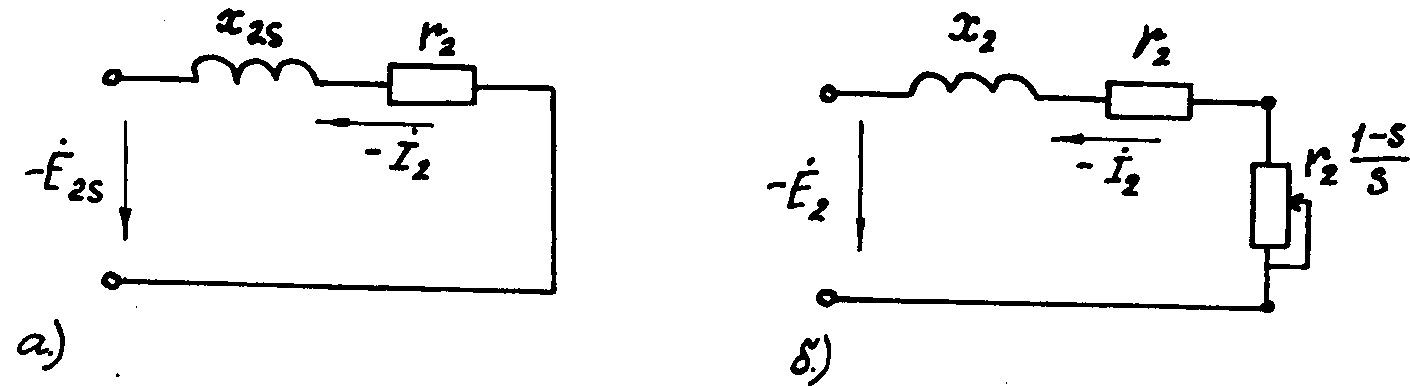
рис. 2а.

Рис.2. Схемы замещения вращающегося (а) и неподвижного (б) ротора

асинхронного двигателя.

Преобразуем выражение для тока ротора (25). Для этого раз­делим числитель и знаменатель на скольжение S, получим выра­жение для тока I₂ в виде

, (26)

Новому выражению для тока I₂ соответствует схема замещений рис.2б. В этой схеме замещения (по сравнению со схемой рис.2а) на зажимах вместо ЭДС вращения ротора Е_2S=SE₂ с частотой f₂=Sf₁ действует ЭДС при неподвижном роторе Е₂ с частотой f₁. Соответственно, вместо индуктивного сопротивления x_2S=Sx₂ и активного сопротивления r₂ вращающегося ротора име­ют место индуктивное сопротивление x₂ и активное сопротивление r₂/S неподвижного ротора. Активное сопротивление r₂/S мож­но представить в виде суммы двух сопротивлений r₂/S=r₂+r₂(1-S)/S. Введение добавочного сопротивления r₂(1-S)/S в схему замещения не оказывает влияния на фазу тока ротора I₂ относительно ЭДC Е₂. Действительно, из схем замещения рис.2 имеем

tgψ₂=x_2S/r₂=Sx₂/r₂=x₂/(r₂/S), (27)

Очевидно, что при переходе от схемы замещения асинхронной машины при вращающемся роторе рис.2а к схеме замещения при не­подвижном роторе рис.2б токи статора I₁ и ротора I₂ остают­ся неизменными по величине и по фазе, следовательно, не изменят­ся величина потребляемой из сети мощности P₁ (1), электромаг­нитная мощность Р_ЭМ (2), механическая мощность Р_МЕХ (3).

P₁ = m₁U₁I₁cosφ₁;

P_ЭМ = P₁ - ΔP_Э1 - ΔP_M1;

P_МЕХ = P_ЭМ - ΔP_Э2 = P₁ - ΔP_Э1 - ΔP_Э2ΔP_M1.

Так как в эквивалентном режиме при неподвижном роторе потери в статоре и роторе остаются такими же, как во вращающейся асинхронной машине, то мощность, потребляемая в добавочном сопротив­лении r₂(1-S)/S, равна полной механической мощности P_МЕХ, развиваемой асинхронной машиной при вращении

, (28)

1.5. Т-образная и Г-образная схемы замещения асинхронной машины

Как уже отмечалось, в неподвижном асинхронном двигателе электромагнитные процессы протекают, в основном так же, как в трансформаторе. В таком случае для анализа электромагнитных про­цессов в эквивалентной асинхронной машине с неподвижным ротором может быть использована Т-образная схема замещения трансформато­ра.

При составлении схемы замещения асинхронной машины рис.3 также, как в теории трансформаторов, обмотка ротора с числом фаз m₂ и числом витков в фазе w₂, заменяется приведенной об­моткой, имеющей число фаз m₁ и число витков фазы w₁, как у обмотки статора.

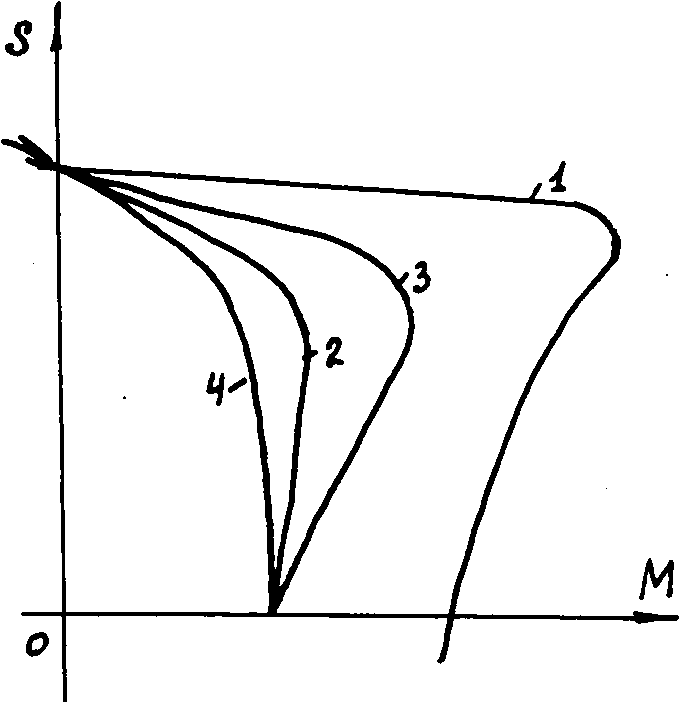
Рис.13. Влияние на механические характеристики асинхронного двигателя добавочного сопротивления, включенного в цепь статора. 1 - естественная характеристика; 2 - Z_доб=r_доб; 3 - Z_доб=x_доб; 4 – U₁<U_1НОМ