3. Выборочная средняя, мода, медиана, выб. Дисперсию, выб. Среднее квадратическое отклонение, исправленную выб. Дисперсию, коэф. Асимметрии и эксцесса;
Xi |
Ni |
Ni*Xi |
(Xi-Xср) |
(Хi-Xср)^2 |
Ni*(X-Xср)^2 |
14,34 |
8 |
114,72 |
-13,8485 |
191,781 |
1534,247618 |
16,51 |
8 |
132,08 |
-11,6785 |
136,3874 |
1091,098898 |
22,43 |
13 |
291,59 |
-5,7585 |
33,16032 |
431,0841893 |
26,69 |
23 |
613,87 |
-1,4985 |
2,245502 |
51,64655175 |
30,86 |
22 |
678,92 |
2,6715 |
7,136912 |
157,0120695 |
34,94 |
11 |
384,34 |
6,7515 |
45,58275 |
501,4102748 |
39,11 |
11 |
430,21 |
10,9215 |
119,2792 |
1312,070785 |
43,28 |
4 |
173,12 |
15,0915 |
227,7534 |
911,013489 |
|
100 |
2818,85 |
|
|
5989,583875 |
Xcp |
28,1885 |
Mo |
25 |
Me |
28,7 |
Dвыб |
59,8958 |
σ |
7,73924 |
|
60,5009 |
Ассиметрия |
-0,1007 |
Эксцесс |
-0,6434 |
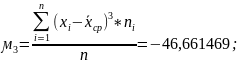
Мера остроты пика распределения случайной величины достаточно высокая
Асимметрия левосторонняя, о чем свою очередь свидетельствует отрицательное значение.
4. Проверить с помощью критерия Пирсона гипотезу о нормальном распределении генеральной совокупности
Xi |
Ni |
(X-Xср) |
Ui |
ᶲ(Ui) |
(Ni-n’i)^2 |
(Ni-n’i)^3 |
14,34 |
8 |
-13,8485 |
-1,78939 |
0,0804 |
4,332053 |
3,105648 |
16,51 |
8 |
-11,6785 |
-1,509 |
0,1276 |
6,875249 |
0,184003 |
22,43 |
13 |
-5,7585 |
-0,74407 |
0,3034 |
16,34757 |
0,685499 |
26,69 |
23 |
-1,4985 |
-0,19362 |
0,3918 |
21,11068 |
0,169087 |
30,86 |
22 |
2,6715 |
0,345189 |
0,3752 |
20,21625 |
0,157387 |
34,94 |
11 |
6,7515 |
0,872372 |
0,2732 |
14,72036 |
0,940268 |
39,11 |
11 |
10,9215 |
1,411185 |
0,1476 |
7,952874 |
1,1675 |
43,28 |
4 |
15,0915 |
1,949998 |
0,0596 |
3,211323 |
0,193693 |
Хнаб^2=6,6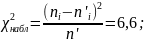
Xкр^2=11,1
Отсюда видно, что χкр^2 >χнаб^2, значит делаем вывод, что гипотезу о нормальном распределении можно принять.
5. Построить кривую Гаусса
X |
12,71 |
20,45 |
28,19 |
35,93 |
43,67 |
Y |
0,007 |
0,032 |
0,052 |
0,032 |
0,007 |
6. Оценить с надежностью γ=0,95 математическое ожидание a и среднее квадратическое отклонение σ нормально распределенного признака генеральной совокупности с помощью доверительных интервалов
t |
1,984 |
t(s/(n^1/2)) |
1,543201 |
q |
0,143 |
110,1463621 |
<a< |
114,9736379 |
10,60667537 |
<σ< |
14,14635934 |
при
q<1;