Международный университет природы, общества и человека «Дубна»

Кафедра прикладной математики и информатики

Курсовая работа

по математической статистике

на тему:

«Статическая обработка результатов проверки сосудов Дьюара для хранения жидкого азота, при проверке количества испаряющегося азота »

Выполнил: студент гр.2241

Казарцев С.В.

Руководитель: доц. Богомолова Е.В.

Дубна, 2014 Задача 1. Теоретическая часть

Если изучаемая случайная величина является непрерывной, то ранжирование и группировка наблюдаемых значений зачастую не позволяют выделить характерные черты варьирования ее значений. Это объясняется тем, что отдельные значения случайной величины могут как угодно мало отличаться друг от друга и поэтому в совокупности наблюдаемых данных одинаковые значения величины могут встречаться редко, а частоты вариантов мало отличаются друг от друга.

Нецелесообразно также построение дискретного ряда для дискретной случайной величины, число возможных значений которой велико. В подобных случаях следует строить интервальный вариационный ряд распределения.

Для построения такого ряда весь интервал варьирования наблюдаемых значений случайной величины разбивают на ряд частичных интервалов и подсчитывают частоту попадания значений величины в каждый частичный интервал.

1 Интервальный вариационный ряд - совокупность интервалов варьирования значений случайной величины с частотами попаданий в каждый из них значений величины.

Для построения интервального ряда необходимо:

1. определить величину частичных интервалов;

2. определить ширину интервалов;

3. установить для каждого интервала его верхнюю и нижнюю границы;

4. сгруппировать результаты наблюдении.

1

Вопрос о выборе числа и ширины интервалов группировки приходится решать в каждом конкретном случае исходя из целей исследования, объема выборки и степени варьирования признака в выборке.

Приблизительно число интервалов k можно оценить исходя только из объема выборки n :по формуле Стержеса: k = 1 + 3,32·lg n;

2. Обычно предпочтительны интервалы одинаковой ширины. Для определения ширины интервалов h вычисляют:

• размах варьирования R - значений выборки: R = x_max - x_min,

где x_max и x_min - максимальная и минимальная варианты выборки;

• ширину каждого из интервалов h определяют по следующей формуле: h = R/k.

3. Нижняя граница первого интервала x_h1 выбирается так, чтобы минимальная варианта выборки x_min попадала примерно в середину этого интервала: x_h1 = x_min - 0,5·h .

Промежуточные интервалы получают прибавляя к концу предыдущего интервала длину частичного интервала h:

x_hi = x_hi-1 +h .

Построение шкалы интервалов на основе вычисления границ интервалов продолжается до тех пор, пока величина x_hi удовлетворяет соотношению:

x_hi <x_max + 0,5·h .

2

Гистограммой частот -ступенчатая фигура, в основании которой находятся частичные интервалы длиной h, а высоты равны отношению n_i / h

Кумулята представляет собой ломаную, соединяющую точки часто­т и вариантов ряда.

Полигон- ломаную, соединяющую точки плоскости с координатами .

3

Оценка параметров генеральной совокупности

Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение s. Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной.

Точечной оценкой генеральной средней является выборочное среднее  .

Выборочным средним называется среднее арифметическое значение признака выборочной совокупности.

Если все значения x₁, x₂,..., x_n признака выборки различны (или если данные не сгруппированы), то:

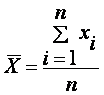
Если же все значения признака x₁, x₂,..., x_n имеют соответственно частоты n₁, n₂,..., n_k, причем n₁ + n₂ +...+ n_k = n (или если выборочное среднее вычисляется по вариационному ряду), то

В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего   значениями вариант считают середины интервалов.

Выборочное среднее является основной характеристикой положения, показывает центр распределения совокупности, позволяет охарактеризовать исследуемую совокупность одним числом, проследить тенденцию развития, сравнить различные совокупности (выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0).

Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения.

Выборочной дисперсией D_в называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения  .

Если все значения x₁, x₂,..., x_n признака выборки объема n различны, то:

Если же все значения признака x₁, x₂,..., x_n имеют соответственно частоты n₁, n₂,..., n_k, причем n₁ + n₂ +...+ n_k = n, то

Среднее квадратическое отклонение (стандартное отклонение) вычисляется как корень квадратный из дисперсии.

Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.

Непараметрическими характеристиками положения являются мода и медиана.

Модой M_o называется варианта, имеющая наибольшую частоту или относительную частоту.

Медианой M_e называется варианта, которая делит вариационный ряд на две части, равные по числу вариант.

При нечетном числе вариант (n=2k+1)

M_e = x_k+1,

а при четном числе вариант (n=2k)

M_e = (x_k + x_k+1)/2.

4

Исправленная выборочная дисперсия вычисляется по формуле:

5

Ассиметрия-отсутствие или нарушение симметрии.

Эксцесс- мера сплюснутости функции.

Найдем центральные эмпирические моменты третьего и четвертого порядка:      

     _{Найдем значение коэффициента асимметрии и эксцесса:}      

₆

Критерий согласия Пирсона (хи-квадрат) служат для проверки нулевой гипотезы H₀: генеральная совокупность Х имеет нормальное распределение.

и _{нам уже известны, дальше}

_{перейдем к нормированным вариантам} , вычислим теоретические частоты n’_i=nP_i. И по формулам выислим:

7 Говорят, что случайная величина нормально распределена или подчиняется закону распределения Гаусса, если ее плотность распределения имеет вид

, где a– математическое ожидание, а σ – стандартное отклонение.

Доверительным называется интервал, который с заданной надежностью   покрывает оцениваемый параметр.

Для оценки математического ожидания   случайной величины  , распределенной по нормальному закону, при известном среднем квадратическом отклонении   служит доверительный интервал

где   - точность оценки,   - объем выборки,   - выборочное среднее,   - аргумент функции Лапласа, при котором 

Интервальной оценкой (с надежностью γ) среднего квадратическогоотклонения нормально распределенного количественногопризнака X по «исправленному» выборочному среднему квадратическому отклонению s служит доверительный интервал:

(при q<1) и (при q>1).