
- •Застосування інформаційних технологій (AutoCad) у кінематичному аналізі важільних механізмів в задачах інженерної механіки
- •Передмова
- •Розділ і. Структурний та кінематичний аналіз механізму
- •Завдання
- •Провести кінематичне дослідження механізма компресора методом планів.
- •Структурний аналіз механізма
- •Побудова планів положень механізма
- •Побудова планів швидкостей
- •Побудова планів прискорень
- •Розділ іі. Основні відомості про графічний редактор AutoCad
- •Запуск AutoCad
- •Основні елементи вікна AutoCad
- •Початок роботи
- •Установка типу і точності представлення одиниць вимірювання
- •Границі креслення
- •Установка режиму крокової прив’язки
- •Режим Ortho
- •Робота з командами
- •Задання координат точок на кресленні
- •Побудова елементарних графічних об’єктів (примітивів)
- •Побудова полілінійних об’єктів та сплайнів
- •Багатокутник
- •Прямокутник
- •_Rectang Первый угол или [Фаска/Уровень/Сопряжение/Высота/Ширина]:
- •Команда «Поделить»
- •Команда «Разметить»
- •Команди редагування об’єктів
- •Команда „Стереть”
- •Команда „Перенести”
- •Команда „Копирование”
- •Буфер обміну Windows
- •Команда «Подобие»
- •Команда «Поворот»
- •Команда «Зеркало»
- •Команда «Массив»
- •Команда «Растянуть»
- •Команда «Обрезать»
- •Команда «Удлинить»
- •Команда «Масштаб»
- •Команда «Расчленить»
- •Додатковий засіб редагування «Ручки»
- •Текст на кресленні
- •Однорядковий текст
- •Вирівнювання
- •Багаторядковий текст
- •Текстові стилі
- •Редагування тексту
- •Точність графічних побудов на кресленні. Об’єктна прив’язка
- •Шари креслення
- •Властивості об’єктів
- •Штриховка
- •Розділ іii. Зміст завдання
- •Вимоги до оформлення розрахунково-пояснювальної записки
- •Вимоги до оформлення графічної частини розрахунково-графічної роботи
- •Завдання до виконання розрахунково-графічної роботи
- •Зразок оформлення титульного аркуша ргр
- •Бібліографічний список
Побудова планів прискорень
Побудова планів прискорень розглядається для II положення механізма (див. креслення-вкладку) і здійснюється в такій послідовності.
5.1.
Кривошип ОА
обертається рівномірно (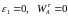 ).
У цьому випадку прискорення точки А
ланки 1 дорівнює її нормальному
прискоренню (напрямлено до центра
обертання О),
тобто
).
У цьому випадку прискорення точки А
ланки 1 дорівнює її нормальному
прискоренню (напрямлено до центра
обертання О),
тобто
 .
.
5.2. Визначається масштаб плану прискорень:
 ,
,
де
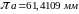 − довжина відрізка, що зображує вектор
прискорення
− довжина відрізка, що зображує вектор
прискорення
 на плані прискорень. Його довжина
вибирається за таким же принципом, як
довжина відрізка
на плані прискорень. Його довжина
вибирається за таким же принципом, як
довжина відрізка
 на плані швидкостей.
на плані швидкостей.
5.3. Визначається прискорення точки В. Точка В є спільною для ланок АВ і ВС, тому її рух залежить від руху цих ланок одночасно.
а) Розглядаємо рух ланки АВ. Вона здійснює плоскопаралельний рух. Приймаємо за центр обертання точку А і записуємо рівняння:
 ,
(4)
,
(4)
де
 та
та
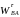 − відповідно нормальне і тангенціальне
прискорення точки В
відносно точки А.
− відповідно нормальне і тангенціальне
прискорення точки В
відносно точки А.
Прискорення
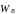 зображується на плані прискорень
відрізком
зображується на плані прискорень
відрізком
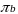 ,
,
 ,
,
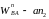 ,
а
,
а
 ,
так що останнє рівняння у відрізках
плану прискорень запишеться
,
так що останнє рівняння у відрізках
плану прискорень запишеться
 .
(4')
.
(4')
Визначаємо модулі векторів.
Нормальне
(або доцентрове) прискорення
 направлено від точки В
до точки А
і дорівнює
направлено від точки В
до точки А
і дорівнює
 .
.
Довжина
відрізка
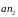 ,
що зображує вектор цього прискорення
на плані прискорень
,
що зображує вектор цього прискорення
на плані прискорень
 .
.
Тангенціальне
(або дотичне) прискорення
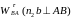 має напрям перпендикулярний до ланки
АВ
і за модулем невідомо.
має напрям перпендикулярний до ланки
АВ
і за модулем невідомо.
б) Розглядаємо рух ланки ВС. Вона теж здійснює плоскопаралельний рух. Приймаємо за центр обертання точку С і записуємо рівняння:
 ,
(5)
,
(5)
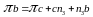 ,
(5')
,
(5')
де
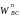 та
та
 − відповідно нормальне і тангенціальне
прискорення точки В
відносно точки С.
− відповідно нормальне і тангенціальне
прискорення точки В
відносно точки С.
Визначаємо модулі векторів.
Прискорення
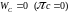 .
.
Нормальне
прискорення
 направлено від точки В
до точки С
і дорівнює
направлено від точки В
до точки С
і дорівнює
 .
.
Довжина
відрізка
 ,
що зображує вектор цього прискорення
на плані прискорень
,
що зображує вектор цього прискорення
на плані прискорень
 .
.
Тангенціальне
прискорення
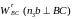 має напрям перпендикулярний до ланки
ВС
і за модулем невідомо.
має напрям перпендикулярний до ланки
ВС
і за модулем невідомо.
Побудова
плану прискорень. На площині довільно
вибираємо полюс
 .
Від нього відкладаємо відрізок
.
Від нього відкладаємо відрізок
 паралельно ОА,
у напрямі від точки А
до точки О
. Оскільки прискорення точки О
(як і точки С)
дорівнює нулю, то відповідна точка о
( с
) співпадає з полюсом
.
Згідно з векторними рівняннями (4'),
(5')
від точки а
відкладаємо в напрямі від В
до А
відрізок
паралельно ОА,
у напрямі від точки А
до точки О
. Оскільки прискорення точки О
(як і точки С)
дорівнює нулю, то відповідна точка о
( с
) співпадає з полюсом
.
Згідно з векторними рівняннями (4'),
(5')
від точки а
відкладаємо в напрямі від В
до А
відрізок
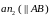 ,
а від полюса
у напрямі від В
до С
відрізок
,
а від полюса
у напрямі від В
до С
відрізок
 .
З точки
.
З точки
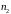 проводимо пряму, перпендикулярну АВ
(
проводимо пряму, перпендикулярну АВ
(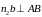 ),
а з точки
),
а з точки
 − перпендикулярну ВС
(
− перпендикулярну ВС
( ).
На їх перетині знаходимо точку b.
).
На їх перетині знаходимо точку b.
Модулі прискорень визначаються з плану:

5.4 Теорема подібності для планів прискорень: план прискорень ланки подібний їй і повернутий відносно неї.
Прискорення точки D2 (ланки АВ), з якою в даний момент співпадає повзун D, визначається за допомогою властивості подібності картини відносних прискорень фігур і ланки (теорема подібності для планів прискорень) і знаходиться із співвідношення:
,
звідки
 .
.
Значення AD2 = 12,5588 мм береться безпосередньо з креслення (див. Плани положень механізма).
Відрізок
 ,
проведений з полюса плану в точку d2,
зображує вектор прискорення точки D2.
Його значення береться з креслення
(див. Плани прискорень).
Абсолютне значення прискорення
,
проведений з полюса плану в точку d2,
зображує вектор прискорення точки D2.
Його значення береться з креслення
(див. Плани прискорень).
Абсолютне значення прискорення
 .
.
5.5. Прискорення точки D повзуна, який здійснює складний рух, визначається за теоремою Коріоліса:
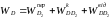 ,
(6)
,
(6)
 ,
(6')
,
(6')
де
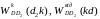 − прискорення Коріоліса та відносне
прискорення точки D
повзуна відносно D2
ланки 2.
− прискорення Коріоліса та відносне
прискорення точки D
повзуна відносно D2
ланки 2.
Коріолісове прискорення
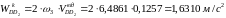 .
.
Відрізок
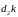 ,
що зображує коріолісове прискорення
,
що зображує коріолісове прискорення
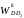 на плані прискорень
на плані прискорень
 .
.
Вектор
коріолісового прискорення має напрям
вектора відносної швидкості
 ,
попередньо повернутого в бік переносної
кутової швидкості
на 90º. В положенні ІІ, яке розглядається,
вектор коріолісового прискорення
має напрямок
перпендикулярно до ланки АВ униз.
,
попередньо повернутого в бік переносної
кутової швидкості
на 90º. В положенні ІІ, яке розглядається,
вектор коріолісового прискорення
має напрямок
перпендикулярно до ланки АВ униз.
Відносне
прискорення
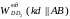 має напрям вздовж ланки АВ
і за модулем невідомо.
має напрям вздовж ланки АВ
і за модулем невідомо.
Абсолютне
прискорення
 точки D,
як точки, що належить ланці DЕ,
має напрям вздовж неї (поступальний
рух), тобто вертикальний.
точки D,
як точки, що належить ланці DЕ,
має напрям вздовж неї (поступальний
рух), тобто вертикальний.
Згідно
з рівнянням (6')
з точки d2
відкладається відрізок
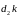 ,
що зображує коріолісове прискорення
,
через точку k
проводиться паралельно
ланці АВ
лінія дії відносного прискорення
,
що зображує коріолісове прискорення
,
через точку k
проводиться паралельно
ланці АВ
лінія дії відносного прискорення
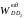 ,
а через полюс плану – пряма, паралельна
DЕ.
В перетині одержується точка d.
З’єднуючи точку d
з полюсом плану, отримують відрізок
,
а через полюс плану – пряма, паралельна
DЕ.
В перетині одержується точка d.
З’єднуючи точку d
з полюсом плану, отримують відрізок
 ,
що зображує абсолютне прискорення точки
D.
,
що зображує абсолютне прискорення точки
D.
Модуль
прискорення
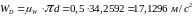 .
.
5.6. Кутові прискорення ланок.
Кутове
прискорення ланки АВ:
 .
.
Для
визначення напряму кутового прискорення
 точку В
разом з шатуном 2 повертаємо уявно
навколо нерухомої у відносному русі
точки А
в напрямі тангенціального прискорення
точку В
разом з шатуном 2 повертаємо уявно
навколо нерухомої у відносному русі
точки А
в напрямі тангенціального прискорення
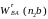 .
Одержаний для даного положення механізму
уявний напрям обертання проти стрілки
годинника визначає напрямок
.
.
Одержаний для даного положення механізму
уявний напрям обертання проти стрілки
годинника визначає напрямок
.
Аналогічно отримуємо кутове прискорення ланки ВС :
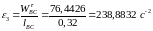 .
.
Напрямок
 − за рухом годинникової стрілки.
− за рухом годинникової стрілки.
Кутове
прискорення ланок 2 і 4 однакові:
 .
.
Ланка
5 рухається поступально, тому
 .
.
Значення прискорень точок і кутових прискорень ланок для всіх положень механізма наведені в табл. 2.
Таблиця 2
Прискорення точок механізма (в м/с2) та
кутові прискорення його ланок (в с-2)
-
Параметр
Положення кривошипа
0
І
ІІ
ІІІ

61,4109

39,0213
0,0007
17,6692
3,6224

11,7715
88,6012
22,5925
18,2953
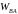
40,7582
88,6012
28,6814
18,6505

8,5659
26,8376
2,3564
45,1318
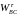
19,0618
8,2764
76,4426
3,8462
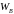
20,8980
28,0848
76,4789
45,2954
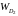
26,3659
19,6389
63,0661
51,6337

25,1330
0,2462
1,6310
24,6891

18,6673
4,0776
66,3729
12,4560

14,7841
18,5864
17,1296
78,6517
- 28,0273
- 210,9551
+ 53,7916
+ 43,5602
+ 59,5680
+ 25,8636
- 238,8832
- 12,0195
Примітка. Знак ”+” відповідає напряму кутового прискорення проти руху годинникової стрілки, “-“ – за рухом годинникової стрілки.
