3.Оценка точности опорных межевых сетей, предназначенных для целей государственного кадастра недвижимости.

Оценка точности заключается в вычислении средних квадратических ошибок следующих элементов проекта геодезической сети: − СКО положения пункта в наиболее слабом месте сети m0; − СКО положения наиболее слабых смежных пунктов mI-J; − СКО дирекционного угла ma I-J; − СКО длины линии msI-J; − СКО определения площади геометрической фигуры, образованной пунктами ГО mp и сравнение их с нормативными величинами. СКО элементов вычисляются по заданной нормативно СКО угловых и линейных измерений (mβ и mL), которые соответствуют запроектиро- ванному классу геодезического построения (см. табл. 2.4, 2.6). В качестве нормативных требований, предъявляемых к геодезическим построениям для целей ГКН, фигурирует СКО положения наиболее слабых смежных пунктов mI-J и СКО определения длины линии в наиболее слабом месте. Оценка точности проекта геодезической сети выполняется на основании теории метода наименьших квадратов, детально изложенной в работах. Основой для выполнения оценки точности является выполненный проект геодезической сети с определенными графически координатами исходных и определяемых пунктов и запроектированные измерения. Оценка точности выполняется на основании принятия гипотезы о нормальном характере распределения случайных ошибок в векторе измерений, который затем будет получен в результате реализации выполненного проекта. Оценка точности необходима для анализа выполненного проекта геодезического построения и определения его соответствия целям и задачам Государственного кадастра недвижимости, создаваемого в заданной территориальной зоне.

Оценка точности – вычисление СКО уравненных элементов и сравнение полученных значений с нормативными допусками. Под СКО понимают: 1) ош. положения пункта относ-но ближайшего исходного (mi); 2) ошибку взаимного положения 2-х определяемых п-тов (mi-j); 3) ош. опред-ния длины линии в относ.мере; 4) ош. ориен-ния направления (mαi-j); 5) ош. опред-я площади структурной единицы город. кадастра (mР). Вычисление СКО элементов выполняется по заданной точности углов и лин. измерений: mβ = Const, mb/b = Const Необходимо найти: mi, mi-j, , mαi-j, mР. Для выполнения оценки точности по схеме запроект. сети необх. составить матрицу весовыхкоэф-тов:Q=(A^T*P*A)^-1 (1)

A – матрица парам. уравнений поправок, кот. в общем виде имеет размерность n*t (Ant); n – число всех запроек. измерений (строк); t – удвоенное число определяемых п-тов (число столбцов).Например,

Ant =А4x2 =

Уравнение поправок для запроект. углов в индексном виде запис-ся след.образом:

V_βk’=(a_kj-a_ki)^.∆x_k+(b_kj-b_ki)^.∆y_k+a_jk^.∆x_j+b_jk^.∆y_j-a_ik^.∆x_i-b_ik^.∆y_i (2)

В уравнении (2) k' обозначает порядк. номер запроект. угла (в примере k' будет меняться от 1 до 3 – 3 угла); индексы k, j, i – обозн-ют название п-тов, кот.образуют запроект. угол (либо пункт 1, 2, 3);

∆x_k,∆y_k; ∆x_j, ∆y_j; ∆x_i, ∆y_i-поправки, приближенные к значениям координат опред-мых п-тов, кот.на этапе оценки точности проекта остаются неизв-ми величинами и кот. обозначают название столбцов матрицы А.

akj, bkj, aik, bik – коэф-ты, кот.необходимо получить в числ. виде и кот. находятся по след. уравнениям (3): 206265 "

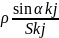a_kj= ; b_kj=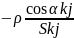 ; 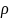=_206265*(a₁₃= )

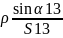αkj, Skj – соотв-но дирекц. угол и длина стороны, кот.измер-ся со схемы запроект. геод. сети. Для преобр-ния уравнения (2) к виду, кот.соотв-етзапроект. измерению, необходимо индексный рисунок положить на схему запроект. сети для соот. измерения. Индекс. рис. (соотв. рис.1):

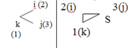
Всоотв. срис.1: V_β1=(a₁₃-a₁₂)∆x₁+(b₁₃-b₁₂)∆y₁+a₃₁^.∆x₃+b₃₁^.∆y₃-a₂₁^.∆x₂-b₂₁∆y₂

При исх. пунктах (1, 2) коэф-ты параметрич. уравнения обнуляются, затем записываем рез-ты в матрицу (a31, b31). Вершиной угла будет уже 2 (а не 1):

V_β2=-a₃₂*^.∆x₃-b_32*∆y₃

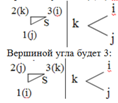
V_β3=(a₃₂-a₃₁) *^.∆x₃+(b₃₂-b₃₁)_*∆y₃

Парам. ур-е поправок для запроект. длин линий в общем виде запис-сяслед.образом:

Парам.ур-е поправок для запроект. длин линий в общем виде запис-ся след. образом: V_S=-cosα_ij∆x_i-sinα_ij∆y_i+cosα_ij∆x_j-sinα_ij∆y_j

Для преобр-ния индексного урав-я (4) к виду, кот.соотв-етзапроект. измерению, необходимо индекс. рис. наложить на схему запроект. сети:

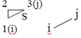
.к. коэф-ты при исх.пунктах обнуляются, то

V_S13=-cosα₁₃∆x₁-sinα₁₃∆y₁+cosα₁₃∆x₃-sinα₁₃∆y₃= cosα₁₃∆x₃-sinα₁₃∆y₃

В урав-ях (3) размерности Skj д/быть такими, чтобы величины коэф. (akj, bkj) были бы как можно ближе к 1.Q=(A^T*P*A)^-1

Р – матрица весов запроект. измерений. В общем виде имеет размер n*n (Р n*n ). Для рис.1 имеет размер 4*4 (Р 4*4 - квадратная матрица). Р n*n = Р 4*4 =

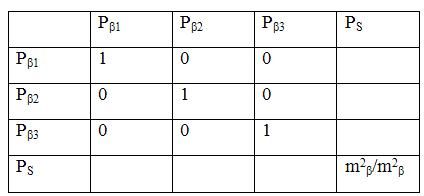
Вес запроект. угла выч-ся по ф-ле:P_βk’=µ²/m²_β (5)

μ – СКО единицы веса. На этапе предвычисления точности она приравн-ся к mβ: μ = mβ (6), т.е. Рβk = 1 (Рβ1=1; Рβ2=1; Рβ3=1).

Вес запроектирован.длины линии вычисляются по ф-ле:

P_s=m_β²/m_β²

На основании условия (6):P_S=µ²/m²_β

В результате решения ур-я (1) получается матрица вес.коэф-ов, кот. имеет размер t*t (2*2 – для данной сети). t*t = Q 2*2 =

На диагонали матрицы Q находятся вес.коэф-ты, кот. определяют точность положения пункта mi (QX3, QY3) .

Ошибка положения пункта по оси х: m_x3= µ _x3 ; по оси ординат: m_y3=µ _y3Ошибка пункта (m_i): m₃=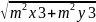 = = µ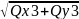

m₃= µ. Т.о. m₃=m_β (7)

Для варианта, когда геод. сеть состоит из неск-ких опред-мых п-тов, ф-ла длявычисления ошибки положения пункта имеет след.вид:

m_i= µ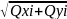 =m_β (8)

В том случае, когда необходимо вычислить ошибку определения пункта в наиболее слабом месте сети, используют макс. сумму диагональных элементов, кот.опред-ет наиболее слабый пункт

m_i=m_β (9)

Заключит.этапом оценки точности явл. сравнение полученных рез-тов с нормативной величиной.