Реализация овощной продукции

Товар	Реализация в текущем периоде, руб. p1q1	Изменение цен в текущем периоде по сравнению с базисным, % ip*100%-100%	Расчетные графы
			ip	p1q1 / ip
Морковь	23 000	+4,0	1,040	22 115
Свекла	21 000	+2,3	1,023	20 528
Лук	29 000	-0,8	0,992	29 234
итого	73 000	х	х	71 877

Решение: вычислим средний гармонический индекс

I_p = = = 1.016 или 101,6 %

Цены по данной товарной группе в текущем периоде по сравнению с базисным в среднем возросли на 1,6%.

При расчете свободного индекса физического объема товарооборота (I_{q =} ) можно использовать среднюю арифметическую формулу. При этом в числителе производиться замена: q₁= i_q q₀. Тогда индекс имеет вид:

I_q =

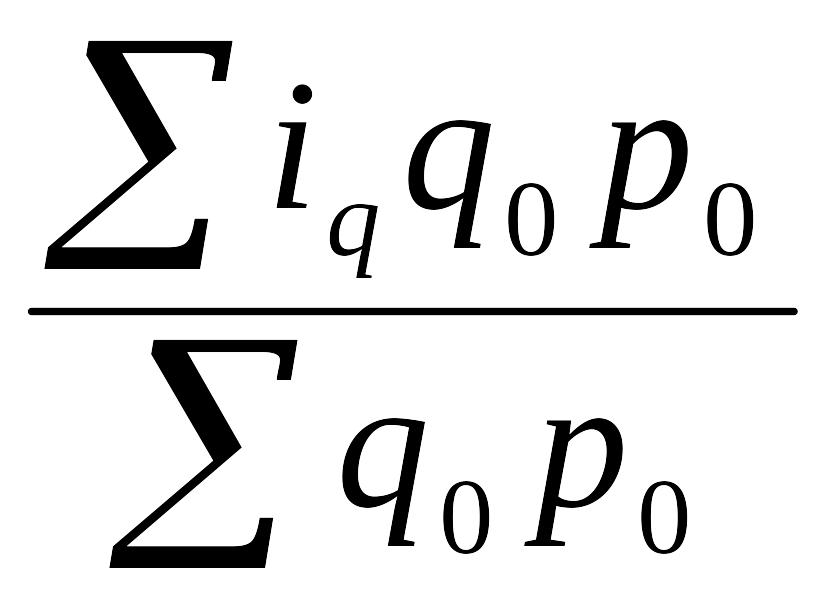
Пример. Предположим, что в нашем распоряжении имеются данные:

Реализация товаров в натуральном и стоимостном выражении

Товар	Реализация в базисном периоде, руб q0p0	Изменение физического объема реализации в текущем периоде по сравнению с базисным, % Ip*100%-100%	Расчетные графы
			ip	p1q1 / ip
Мандарины	46 000	-6,4	0,936	43 056
Апельсины	51 000	+1,3	1,013	51 663
Грейпфруты	27 000	-8,2	0,918	24 786
Итого	124 000	х		119 505

Рассчитать средний арифметический индекс.

Решение:

I_q = = = 0.964 или 96,4 %

Физический объем реализации данных товаров в среднем снизился на 3,6 %.

В средней арифметической форме также может рассчитываться и индекс производительности труда по трудоемкости, известный как индекс С.Г. Струмилина:

.

Системы индексов.

Индексы могут использоваться для анализа динамики социально-экономических явлений за ряд последовательных периодов. В этом случае для достижения сопоставимости они должны рассчитываться по единой схеме. Такая схема расчета индексов за несколько временных периодов называется системой индексов.

В зависимости от информационной базы и целей исследователя индексная система может строиться в четырех вариантах.

Рассмотрим систему индексов на примере сводного индекса цен, рассчитываемого за "n" периодов:

А. Цепные индексы цен с переменными весами:

. . .

Б. Цепные индексы цен с постоянными весами:

; ; ; . . . .

В. Базисные индексы цен с переменными весами:

; ; ; . . . .

Г. Базисные индексы цен с постоянными весами:

; ; ; . . . .

Индексы постоянного и переменного состава.

Все рассмотренные выше индексы рассчитывались по нескольким товарам, реализуемым в одном месте, или видам продукции, производимым на одном предприятии. Рассмотрим теперь случай, когда один товар реализуется в нескольких местах или вид продукции производится на ряде предприятий.

Если реализуется только один вид продукции, вполне правомерно рассчитывать его среднюю цену в каждом периоде. Индекс переменного состава представляет собой отношение двух полученных средних значений:

.

Данный индекс характеризует не только изменение индивидуальных цен в местах продажи, но и изменение структуры реализации по предприятиям розничной или оптовой торговли, рынкам, городам и регионам. Для оценки воздействия этого фактора рассчитывается индекс структурных сдвигов:

.

Последним в данной системе является рассмотренный выше индекс цен фиксированного состава, который не учитывает изменение структуры:

.

Между данными индексами существует следующая взаимосвязь: .

Пример. Провести анализ изменения цен реализации товара А в двух регионах.

Реализация товара А в двух регионах.

регион	июнь		Июль		Расчетные графы, руб
	Цена, руб p0	Продано, шт. q0	Цена, руб p1	Продано, шт q1	q0p0	q1p1	q1p0
1	12	10 000	13	18 000	120 000	234 000	216 000
2	17	20 000	19	9 000	340 000	171 000	153 000
итого		30 000		27 000	460 000	405 000	369 000

Решение:

Вычислим индекс цен переменного состава:

I^пс_р = : = : = 15,00:15,33=0,978 или 97,8%

Из таблицы видно, что цена в каждом регионе в июле по сравнению с июнем возросла. В целом же средняя цена снизилась на 2,2% (97,8-100). Такое несоответствие объясняется влиянием изменения структуры реализации товаров по регионам: в июне по более высокой цене продавали товара вдвое больше, в июле же ситуация принципиально изменилась (в данном условном примере для наглядности числа подобраны таким образом, чтобы это различие в структуре продаж было очевидным).

Рассчитаем индекс структурных сдвигов:

I_стр = : = : = 0,891 или 89,1%

Первая часть этого выражения позволяет ответить на вопрос, какой бы была средняя цена в июле, если бы цены в каждом регионе сохранились на прежнем июньском уровне. Вторая часть отражает фактическую среднюю цену июня. В целом по полученному значению индекса мы можем сделать вывод, что за счет структурных сдвигов цены снизились на 10,9 %.

Рассчитанный индекс цен фиксированного состава равен 1,098 или 109,8%. Отсюда следует вывод: если бы структура реализации товара А по регионам не изменилась, средняя цена возросла бы на 9,8%. Однако влияние на среднюю цену первого фактора оказалось сильнее, что отражается в следующей взаимосвязи: 1,098*0,891=0,978.

Аналогично строятся индексы структурных сдвигов, переменного и фиксированного состава для анализа изменения себестоимости, урожайности и пр.

Территориальные индексы.

Территориальные индексы служат для сравнения показателей в пространстве, т.е. по предприятиям, округам, городам, районам и пр.

Построение территориальных индексов определяется выбором базы сравнения и весов или уровня, на котором фиксируются веса. При двусторонних сравнениях каждая территория может быть и сравниваемой (числитель индекса), и базой сравнения (знаменатель). Веса как первой, так и второй территории в принципе также имеют равные основания использоваться при расчете индекса. Однако это может привести к различным или даже противоречивым результатам. Избежать подобной неопределенности можно несколькими способами. Один из них заключается в том, что в качестве весов принимаются объемы проданных товаров по двум регионам, вместе взятым:

.

Территориальный индекс цен в этом случае рассчитывается по следующей формуле:

.

Пример. Известны цены и объемы реализации товаров по 2 регионам:

Товар	Регион А		Регион В		Расчетные графы
	Цена, руб pа	Реализа-ция, т qа	Цена, руб pb	Реализа-ция, т qb	Q=qa +qb	Q *pa	Q *pb
1	11,0	30	12,0	35	65	715,0	780,0
2	8,5	45	9,0	50	95	807,5	855,0
3	17,0	15	16,0	90	105	1785,0	1680,0
итого	х	х	х	х	х	3307,5	3315,0

Рассчитать территориальный индекс цен.

Решение:

I_pb/a = = = 1.002 или 100,2%

Цены в регионе В на 0,2% превышают цены в регионе А. Этому выводу не противоречит и обратный индекс:

I_pa/b = = = 0.998 или 99.8%

В формуле данного территориального индекса вместо суммарных иногда используются стандартизованные веса (стандартизованная структура). В качестве таких весов может выступать структура продажи данных видов продукции по более крупному территориальному образованию, например, республике. В этом случае индекс имеет вид:

.

Второй способ расчета территориальных индексов учитывает соотношение весов сравниваемых территорий. При этом способе первый шаг заключается в расчете средней цены каждого товара по двум территориям, вместе взятым:

.

После этого непосредственного рассчитывается территориальный индекс:

.

По данным нашего примера получим:

;

;

.

С учетом рассчитанных средних цен вычислим индекс:

, или 102,2 %.

Данный подход к расчету территориального индекса обеспечивает известную взаимосвязь: .

Индекс физического объема реализации при этом строится следующим образом:

.

Аналогично строятся индексы для сравнения цен территории А с ценами территории Б.