1. 3 Префиксное кодирование, сущность, эффективность

Префиксное кодирование основано на выработке систем кодов переменной длины, которые принято называть системами префиксных кодов (или кодов префикса)[8]. Особенность этих систем состоит в том, что в пределах каждой из них более короткие по длине коды не совпадают с началом (префиксом) более длинных кодов – так называемое свойство префикса.

Системы префиксных кодов обычно получают построением кодовых деревьев. Степень ветвления в этих деревьях зависит от основания системы представления информации. Рассмотрим случай двоичной системы представления, которой соответствуют бинарные кодовые деревья. Как известно, каждый внутренний узел бинарного дерева имеет до двух исходящих ребер. Пронумеруем эти ребра так, чтобы одному из них соответствовал двоичный символ «0», а другому – «1». Так как в дереве не может быть циклов, от корневого узла к листовому узлу всегда можно проложить единственный маршрут. Если ребра дерева пронумерованы, то каждому такому маршруту соответствует некоторая уникальная двоичная последовательность. Множество всех таких последовательностей, очевидно, образует систему префиксных кодов.

Первоначально каждому символу информационного алфавита ставится

в соответствие код нулевой длины («пустой» код) и вес, равный вероятности появления символа на выходе информационного источника в рамках выбранной информационной модели. Все символы алфавита сортируются по убыванию или возрастанию их весов, после чего упорядоченный ряд символов в некотором месте делится на две части так, чтобы в каждой из них сумма весов символов была примерно одинакова. К кодам символов, принадлежащих одной из частей, добавляется «0», а к кодам символов, принадлежащим другой части, добавляется «1» (добавляемое значение формирует очередной крайний правый разряд кода). Как нетрудно понять, каждая из указанных частей сама по себе является упорядоченным рядом символов. Каждый из этих рядов, если он содержит более одного символа, в своюочередьделится на две части в соответствии с описанным выше принципом, и к кодам символов вновь добавляются соответствующие двоичные значения ит.д. Процесс завершается тогда, когда во всех полученных таким образомрядах остается ровно по одному символу.

Алгоритм Шеннона - Фано в действительности не строит кодовое дерево, однако его работу можно проиллюстрировать таким построением[7]. При разделении группы символов происходит как бы разветвление некоторого узла бинарного дерева (листовой узел становится узлом родителем для двух новообразованных дочерних узлов), а присвоение нулей и единиц равносильно установлению соответствия между кодами и маршрутами движения по дереву от корневого узла к листовому узлу.

Префиксный код в теории кодирования – это код со словом переменной длины, удовлетворяющий условию Фано.

Условие Фано: неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо другого более длинного кода [9].

Например, если один из символов первичного алфавита имеет код «110», то в качестве кодов для других символов нельзя использовать последовательности «0» и «11», в тоже время последовательности «10» и «0» использовать можно (при условии что они не являются префиксом других кодов символов данного алфавита).

Декодирование префиксных кодов однозначно выполняется слева направо. При этом сопоставление с таблицей кодов всегда дает точное указание конца одного кода и начала следующего. Это дает возможность не использовать разделители.

1. 4 Алгоритм Шеннона – Фано

Алгоритм Шеннона - Фано - один из первых алгоритмов сжатия. Он был разработан независимо друг от друга в 1948 году Клодом Элвудом Шенноном (публикация «Математическая теория связи») и, позже, Уго Фано (опубликовано как технический отчёт) [1].

Данный алгоритм основывается на первой теореме Шеннона, которая называется также основной теоремой о кодировании при отсутствии помех, формулируется следующим образом:

«При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак кодируемого алфавита, будет сколь угодно близко к отношению средних информаций на знак первичного и вторичного алфавитов» [10].

Используя понятие избыточности кода, можно дать более короткую формулировку теоремы:

«При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю».

Алгоритм Шеннона - Фано использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся - кодом большей длины.

Коды Шеннона - Фано префиксные, то есть никакое кодовое слово не является префиксом любого другого. Это свойство позволяет однозначно декодировать любую последовательность кодовых слов. Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. В отличие от алгоритма Шеннона - Фано, этот алгоритм остаётся всегда оптимальным и для вторичных алфавитов m₂ с более чем двумя символами.

Кодирование Шеннона – Фано относится к вероятностным методам сжатия, точнее, методам контекстного моделирования нулевого порядка. Этот алгоритм использует избыточность сообщения, заключённую в неоднородном распределении частот символов его первичного алфавита, то есть заменяет коды более частых символов короткими двоичными последовательностями, а коды более редких символов - более длинными двоичными последовательностями.

Алгоритм представляет собой рекурсивную процедуру, позволяющую на основе заданного вероятностного распределения появления символов на выходе источника информации поэтапно формировать отвечающую ему систему префиксных кодов.

Код Шеннона - Фано строится с помощью дерева или таблицы. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева. Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0 [4].

При построении кода Шеннона - Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне может ухудшить варианты разбиения на следующем уровне и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона - Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннон - Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона - Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.

Алгоритм кодирования:

1. Выписываются в ряд символы алфавита в порядке уменьшения их вероятности появления

2. Множество символов алфавита последовательно делятся на два подмножества, так чтобы сумма вероятностей появления символов одного подмножества была равна (или примерно равна) сумме вероятностей появления символов другого подмножества. Для первого подмножества, каждому символу приписывается код «0», а для второго – «1»

3. Разбиения на подмножества повторяются до тех пор, пока все не будут состоять из одного элемента.

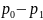
Когда размер подалфавита становится равен нулю или единице, то дальнейшего удлинения префиксного кода для соответствующих ему символов первичного алфавита не происходит, таким образом, алгоритм присваивает различным символам префиксные коды разной длины. На шаге деления алфавита существует неоднозначность, так как разность суммарных вероятностей может быть одинакова для двух вариантов разделения (учитывая, что все символы первичного алфавита имеют вероятность больше нуля).

Пример кодового дерева.

Исходные символы: A,B,C,D,E,F

0

1

1

0

1

0

1

0

Полученный код: A-11, B-101, C-100, D-00, E-011, F-010