Теорема Гюйгенса — Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

,

где  — полная масса тела.

8) Закон Сохранения Импульса

Импульсом называют векторную величину, равную произведению массы тела на ее скорость:

При взаимодействии тел замкнутой системы полный импульс системы остается неизменным:

Закон сохранения импульса есть следствие второго и третьего законов Ньютона. Пример использования закона сохранения импульса.

Рассмотрим неупругое столкновение, при котором выполняется закон сохранения импульса. Пусть при абсолютно неупругом столкновении двух тел их скорость будет общей после удара. Ее нужно определить. Напишем векторное уравнение, соответствующее закону сохранения импульса системы:

После проецирования векторов на выбранную ось получим скалярное уравнение, которое позволит определить искомую величину v_общ. Еще один пример - реактивное движение. Рассмотрим простейший случай этого движения, при котором происходит одномоментное взаимодействие - выстрел из винтовки.

До выстрела скорости винтовки и пули были равны нулю. После выстрела они имели различные скорости. Если известна скорость пули, ее масса и масса ружья, можно определить скорость, которую приобрело ружье после выстрела:

Отсюда после проецирования векторов на выбранную ось получим:

Момент импульса материальной точки относительно точки O определяется векторным произведением , где   — радиус-вектор, проведенный из точки O,   — импульс материальной точки. Момент импульса материальной точки относительно неподвижной оси    равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса    не зависит от положения точки O на оси z.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что  , получим .

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):  .

Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело: .

Применение законов сохранения к решению задач по механике

Для решения задач с использованием закона сохранения импульса, так же, как и в задачах, решаемых с помощью законов Ньютона, следует выбрать инерциальную систему отсчета и рассмотреть замкнутую систему тел.

Для приближенного решения практических задач можно при соблюдении ряда условий применять закон сохранения импульса и в незамкнутых системах. К таким условиям относятся малое время действия внешних сил и их малая величина по сравнению с внутренними силами.

Кроме того, встречаются случаи, когда при несохранении полного импульса в незамкнутой системе, некоторые проекции этого импульса на выбранные направления, вдоль которых сумма внешних сил равна нулю, остаются постоянными.

На чертежах, иллюстрирующих решение задач, необходимо изображать направления для проецирования скоростей и импульсов, а также сами скорости и (или) импульсы тел.

При решении же, вместо законов Ньютона надо записывать закон сохранения импульса, сначала в векторной форме, а затем в проекциях на выбранные направления.

Проиллюстрируем сказанное на конкретных примерах.

9) Единая мера различных форм движения материи называется энергией. Энергия системы материальных тел характеризует эту систему с точки зрения возможных в ней количественных и качественных превращений движения. Эти превращения обусловлены как взаимодействием тел системы между собой, так и с внешними по отношению с системе телами.       Движение является неотъемлемым свойством материи. Поэтому всякое тело обладает энергией, являющейся мерой его движения. Для количественной характеристики качественно различных форм движения, изучаемых в физике, вводятся соответствующие им виды или формы энергии – механическая, внутренняя, электромагнитная и другие.       Причиной изменения состояния механического движения тела, а, следовательно, и его энергии, является взаимодействие тела с другими телами. Для характеристики воздействия этих тел на рассматриваемое тело в механике введено понятие силы. Поэтому можно говорить, что изменение движения и энергии вызывается силами. Процесс изменения энергии тела под действием силы называется процессом свершения работы, а приращение энергии тела в этом процессе называется работой, совершенной силой. Опыт показывает, что сила, приложенная к телу, совершает работу только тогда, если тело при этом перемещается.       Из курса физики средней школы известно, что при прямолинейном поступательном движении тела работа, совершаемая постоянной силой F, тем больше, чем больше составляющая силы F_τ, касательная к траектории и чем больше путь s, пройденный телом за время действия силы:

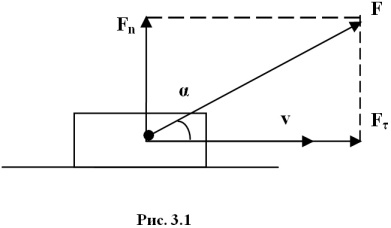
                                                                              (3.1)

      В общем случае сила может изменяться как по величине, так и по направлению, поэтому формула (3.1) является лишь одним из частных случаев. Однако если рассматривать д остаточно малое перемещение, то движение материальной точки можно считать прямолинейным, а силу – постоянной. Поэтому элементарная работа, совершаемая силой F на перемещении dr равна:

                                               (3.1')

      Работа, совершаемая силой F на конечном пути s (путь 1-2 на рис. 3.2), равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках:

                                                        (3.2)

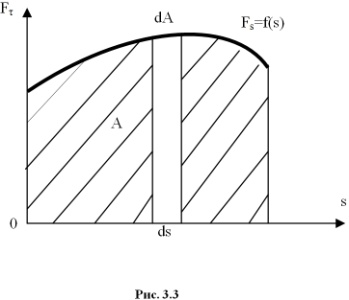
      Для вычисления этого интеграла надо знать зависимость F_τ=∫(s). Очевидно, что работа, совершаемая силой F на пути 0-s, численно измеряется площадью, заштрихованной на рис. 3.3. Если сила F не зависит от s (F_τ=const), то A = F_ss.       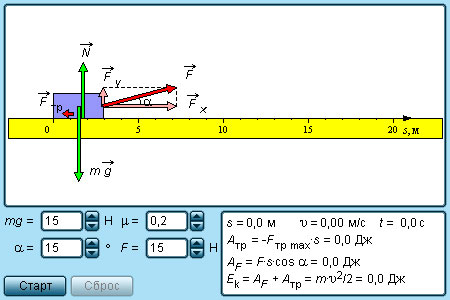Из выражения (3.1') следует, что сила, действующая на тело, не совершает работы, если:       а) тело покоится (ds=0);       б) сила перпендикулярна к направлению перемещения тела (α=90°, F_τ=0).       Если угол α < 90°, то работа силы F положительна (составляющая F_τ совпадает по направлению с вектором скорости v), поэтому в данном случае силу Fназывают движущей силой. Если угол α > 90°, то работа силы F отрицательна (F_τи v противоположны по направлению) и силу F называют силой сопротивления(например, сила трения).       Единица работы – джоуль (Дж): 1 Дж – это работа, совершаемая силой в 1 Н на пути в 1 м:

1 Дж = 1 Н*м.

      Если на тело, движущееся поступательно, одновременно действует несколько сил (рис. 3.4), то работа равнодействующей силы равна алгебраической сумме работ составляющих сил:

      Если работа, совершаемая силой F при перемещении точки из одного произвольного положения 1 в другое произвольное положение 2 (рис. 3.5), не зависит от траектории перемещения, т.е. выполняется условие

0 А_1-2 = А_1-а-2 = А_1-b-2,

то такая сила называется консервативной (или потенциальной).       Из уравнения (3.2) следует, что изменение направления движения вдоль траектории на противоположное вызывает изменение знака работы (cos α меняет свой знак). Поэтому при перемещении материальной точки вдоль замкнутой траектории L, например, 1-a-2-b-1, работа консервативной силы тождественно равна нулю:

                                                        (3.3)

      Примерами консервативных сил являются силы всемирного тяготения, силы упругости, силы электростатического взаимодействия.       Все силы, не удовлетворяющие условию (3.3) (т.е. работа этих сил зависит от траектории перемещения точки), называются неконсервативными или диссипативными. Примером таких сил являются силы трения, которые всегда направлены в сторону, противоположную направлению движения (cos α = -1 ) . Поэтому работа сил трения при перемещении материальной точки вдоль замкнутой траектории всегда отрицательна и никогда не равна нулю.       Для характеристики скорости совершения работы силой F, вводится понятие мощности, численно равной работе, совершаемой силой за единицу времени:                                                                                                                       (3.4)       Подставляя в (3.4) выражение (3.1') для элементарной работы, получим:                                 (3.5)       Следовательно, мощность (мгновенная мощность) силы равна произведению касательной составляющей силы и скорости движения, т.е. скалярному произведению векторов силы и скорости. Если P≠const, то пользуются понятием средней мощности за некоторый промежуток времени t, в течение которого сила совершила работу А:                                                                                                                        (3.6)       Единица мощности – ватт (Вт): 1 Вт – мощность, при которой за время 1 с совершается работа 1 Дж:

1 Вт = 1 Дж/с.

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.

Работой A, совершаемой постоянной силой   называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус углаα между векторами силы   и перемещения   (рис. 1.18.1): 

A = Fs cos α.

Работа является скалярной величиной. Она может быть как положительной (0° ≤ α < 90°), так и отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж).

Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.

Рисунок 1.18.1. Работа силы  :

Если проекция   силы   на направление перемещения   не остается постоянной, работу следует вычислять для малых перемещений Δs_i и суммировать результаты: 

Это сумма в пределе (Δs_i → 0) переходит в интеграл.

Графически работа определяется по площади криволинейной фигуры под графиком F_s(x) (рис. 1.18.2).

Рисунок 1.18.2. Графическое определение работы. ΔAi = FsiΔsi

Примером силы, модуль которой зависит от координаты, может служить сила упругости пружины, подчиняющаяся закону Гука. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу   модуль которой пропорционален удлинению пружины (рис. 1.18.3).

Рисунок 1.18.3. Растянутая пружина. Направление внешней силы   совпадает с направлением перемещения     k – жесткость пружины.

Зависимость модуля внешней силы от координаты x изображается на графике прямой линией (рис. 1.18.4).

Рисунок 1.18.4. Зависимость модуля внешней силы от координаты при растяжении пружины

По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины: 

Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы   равна по модулю работе внешней силы   и противоположна ей по знаку.

Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил.

Модель. Механическая работа

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа: