Практическое задание 2. «Вычисление основных статистических характеристик по результатам тестирования: оценка нормальности распределения» Цель занятия

Оценка нормальности распределения результатов тестирования с использованием коэффициентов асимметрии и эксцесса.

Краткие теоретические сведения

В основу методов описательной статистики, положено предположение о том, что исследуемые признаки распределены по нормальному закону распределения

Нормальное распределение характеризуется средним арифметическим (математическим ожиданием) m и стандартным (среднеквадратичным) отклонением r. Краткое обозначение распределения N(m,r²), где r² - дисперсия. График (рис. 1) нормального распределения симметричен относительно центра распределения (точки m), чем меньше r, тем больше вероятность появления случайной величины.

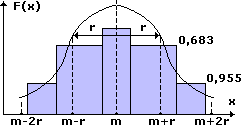
Рис. 1. Нормальное распределение

Характерное свойство нормального распределения состоит в том, что 68% всех его наблюдений лежат в диапазоне [m-r,m+r] , 95,5% - в диапазоне [m-2r,m+2r], 99,7% - в диапазоне [m-3r,m+3r] (так называемое правило трех сигм) .

Рассмотренное свойство лежит в основе различных прикладных статистических методов, в том числе и инструментах оценки качества (гистограммах, картах Шухарта и др.)

Так, анализ гистограмм позволяет произвести оценку степени соответствия выборки известному теоретическому распределению, в частности нормальному распределению, на основе графического представления (рис. 2.).

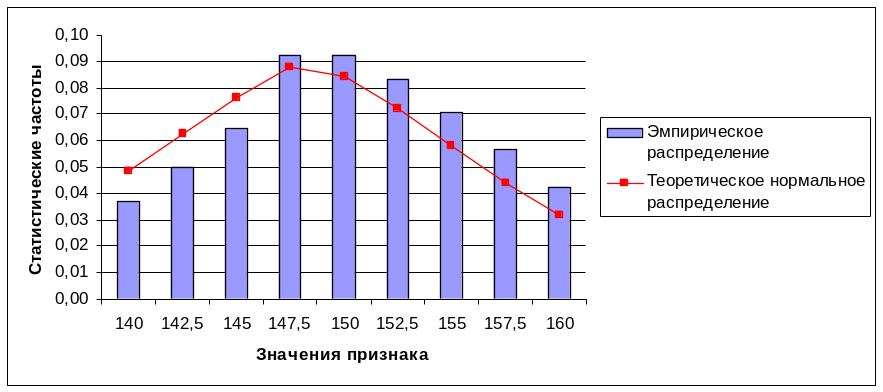
Рис.2. Пример оценки степени соответствия выборки известному теоретическому распределению посредством гистограммы

Как видно из рисунка, эмпирическое распределение напоминает форму нормальной кривой, однако различия присутствуют.

Выводы, сделанные на основе графического представления данных можно подкрепить путем расчета таких числовых характеристик как асимметрия и эксцесс.

Асимметрия – показатель, отражающий перекос распределения относительно среднего арифметического влево или вправо. В тех случаях, когда какие-нибудь причины благоприятствуют более частому появлению значений, которые выше или, наоборот, ниже среднего, образуются асимметричные распределения.

При положительной асимметрии в распределении чаще встречаются более низкие значения признака, а при отрицательной - более высокие.

Сильная асимметрия встречается в специфических выборках. Если мы возьмем учеников-отличников и измеряем IQ, то вероятно получим распределение, скошенное вправо (в сторону высоких баллов). Так же, изучая экстраверсию менеджеров, мы, скорее всего получим скошенное распределение в сторону сильной экстраверсии, т. к. большая часть менеджеров общительные люди.

Эксцесс – показатель, отражающий высоту распределения. В тех случаях, когда какие-либо причины способствуют преиму­щественному появлению средних или близких к средним значений, об­разуется распределение с положительным эксцессом. Если же в рас­пределении преобладают крайние значения, причем одновременно и бо­лее низкие, и более высокие, то такое распределение характеризуется отрицательным эксцессом и в центре распределения может образоваться впадина, превращающая его в двувершинное.

Можно говорить о нормальности распределения, если асимметрия находится в интервале [–0.2;+0.2], а эксцесс – в интервале [2;4].