3.2 Расчет зубчатой конической прямозубой передачи

Материал зубчатых колёс выбираем по таблице 9.6 [2]: для шестерни – сталь 40Х улучшенную 270НВ, , ; для колёс - сталь 40Х улучшенную 260НВ, , .

Определяем допускаемые контактные напряжения по формуле 9.30 [2]. Предел контактной выносливости

для шестерни ;

для колеса .

Эквивалентное число циклов перемены напряжения согласно циклограмме нагружения для колеса и шестерни тихоходной ступени соответственно:

;

где

ч.

с=1 – число колес, находящихся в зацеплении с расчетным

По рис. 9.9 [2] базовое число циклов .

Коэффициент долговечности, учитывающий влияние срока службы и режима нагружения.

для колеса;

для шестерни.

Допускаемые контактные напряжения при коэффициенте безопасности будут равны:

для шестерни - ;

для колеса - .

Среднее значение допускаемых контактных напряжений

.

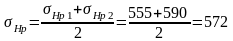Определяем допускаемые напряжения на изгибы по формуле 9.35 [2]:

для колеса: .

для шестерни .

Коэффициент долговечности . С учетом коэффициента безопасности и , коэффициент, учитывающий влияние двустороннего приложения нагрузки получим:

для шестерни - .

для колеса - .

Определяем углы делительных конусов (см. табл. 9.2)[2]:

Определяем средний диаметр шестерни по формуле (9.17)[2]:

где коэффициент, учитывающий неравномерность распределения нагрузки по шири­не венца (см. рис, 9.8)[2]; коэффициент ширины шестерни по фор­муле (9.19)[2].

.

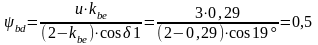Ширина венца

.

Определяем внешний диаметр вершин зубьев

Внешнее конусное расстояние

.

Проверяем рекомендацию табл. 9.2 [2] Условие соблюдается.

Определяем модуль и числа зубьев.

По табл. 9.2 (п.3) [2] внешний окружной модуль . Принимаем .

Число зубьев

.

Определяем биоэквивалентное число зубьев:

С помощью формулы 9.22 производим проверку по контактным напря­жениям (9.22)[2].

Предварительно определяем:

окружное усилие ,

окружная скорость .

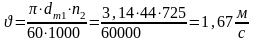По табл. 9.10 [2] назначаем 8-ю степень точности. По табл. 9.9 [2] , по табл. 9.7 б_н =0,006 где, коэффициент, учитывающий влияние разность шагов зацепления зубьев шестерни и колеса, б_н - коэффициент, учитывающий влияние вида зубчатой передачи

Удельная окружная динамическая сила по формуле (9.29) [2].

.

Удельная расчетная окружная сила в зоне ее наибольшей концентрации по формуле (9.16) [2].

По формуле 9.15 [2]

Удельная расчетная окружная сила по формуле 9.25 [2]

Определяем коэффициенты z в формуле (9.22) [2]:

коэффициент, учитывающий механические свойства материала.

коэффициент, учитывающий форму сопряженных поверхностей зубьев;

По формуле (9.24) [2]:

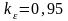, (ст. 191 [2]).

коэффициент, учитывающий суммарную длину контактных линий.

Контактная прочность обеспечена.

По формуле 9.27 производим проверку по напряжениям изгиба:

По графику (см. рис. 9.6)[2] в зависимости от биоэквивалентного числа зубьев находим:

и

Расчет необходимо провести для менее прочного звена, т.е. с наименьшим отношением

-для шестерни; -для колеса;

Расчет ведем по шестерне.

Из графика (см. рис. 9.5 [2]) коэффициент концентрации нагрузки

Удельная окружная динамическая сила по формуле (9.29) [2].

где (см. табл. 9.8 [2]), имеют прежние значения.

Удельная расчетная окружная динамическая сила в зоне ее наибольшей концентрации по формуле по формуле (9.15) [2].

Коэффициент динамической нагрузки по формуле (9.15)[2].

По формуле (9.12) [2]

.

Напряжение изгиба

,

где коэффициент, учитывающий наклон зуба, коэффициент изменения учитывающий перекрытие звеньев.

Условие прочности выполняется. Следовательно, прочность по напряжениям изгиба обеспечена.

Определяем силы в зацеплении.

Окружная сила Н;

Радиальная сила,

Осевая сила

где угол главного профиля зуба (стр.173.[2])