Идеалы. Кольца классов вычетов

Пусть — произвольное кольцо.

Чтобы некоторое подмножество в вновь было кольцом (под- кольцом кольца ), необходимо и достаточно выполнение следую­щих условий:

1) это подмножество должно быть подгруппой аддитивной груп­пы кольца; другими словами, вместе с любыми а и b оно должно содержать разность а - b (свойство модулей)-,

2) вместе с а и b оно должно содержать произведение ab.

Среди подколец особую роль играют подкольца, называемые

идеалами; их роль аналогична роли нормальных подгрупп в теории групп.

Непустое подмножество m кольца называется идеалом, точнее, правым идеалом, если:

1) из следует, что (свойство модулей);

2) из следует для произвольного из . Слова­ми: модуль вместе с каждым своим элементом а должен содер­жать все «правые кратные» .

Равным образом, модуль называется левым идеалом, если из следует для произвольного .

Наконец, подмножество называется двусторонним идеалом, если оно является одновременно правым и левым идеалом.

Для коммутативных колец все три понятия совпадают и поэтому говорят просто об идеалах. Идеалы будут обозначаться строчны­ми готическими буквами.

Примеры идеалов в коммутативных кольцах:

1. Нулевой идеал, состоящий из одного нуля.

2. Единичный идеал , содержащий все элементы кольца.

3. Идеал (а), порожденный элементом а и состоящий из всевоз­можных выражений вида

То, что это множество действительно является идеалом, увидеть легко: разность двух таких выражений имеет, очевидно, тот же вид, а произвольное кратное выглядит так:

т. е. имеет вид

Идеал (а) является, очевидно, наименьшим среди идеалов, содер­жащих элемент а, потому что каждый идеал должен содержать во всяком случае все кратные и все суммы , а по­тому и все суммы вида Идеал (а) может, таким образом, определяться как пересечение всех идеалов, содержащих элемент а.

Если кольцо о обладает единицей е, то для можно воспользоваться записью вида Следова­тельно, в этом случае идеал (а) состоит из всех обычных кратных . Например, идеал (2) в кольце целых чисел состоит из всех четных чисел.

Идеал, порожденный одним элементом а, называется главным. Нулевой идеал всегда главный: это идеал (0). Единичный идеал также является главным, если —кольцо с единицей е, потому что тогда . В некоммутативных кольцах необходимо разли­чать правые и левые главные идеалы. Правый идеал, порожденный элементом а, состоит из всевозможных сумм .

4. Точно так же можно определить левый идеал, порожденный несколькими элементами как совокупность сумм вида

или как пересечение всех левых идеалов кольца о, содержащих элементы Этот идеал обозначают через и го­ворят, что элементы составляют базис этого идеала.

5. Аналогично можно определить левый идеал (М), порожден­ный бесконечным множеством М; он является совокупностью всех конечных сумм вида

Классы вычетов. Любой левый или правый идеал кольца , являясь подгруппой аддитивной группы, определяет некоторое разбиение кольца о на смежные классы или классы вычетов по идеалу . Два элемента а, b называются сравнимыми по идеалу или сравнимыми по модулю , если они принадлежат одному классу вычетов, т. е. если . Обозначение:

или, в краткой форме,

Вместо «а не сравнимо с b» пишут

Если, в частности, — главный идеал ( ) в коммутативном кольце, то вместо можно было бы также писать . Но в целях упрощения записи в этом случае пишут, опуская пару скобок, .

Таким путем приходят, например, к обычным сравнениям по модулю целого числа: (словами: а сравнимо с b по мо­дулю n) означает, что а — b принадлежит идеалу (n), т. е. явля­ется кратным числа n.

Операции над сравнениями. Сравнение по некоторому левому идеалу остается, очевидно, верным, если к обеим частям прибавить один и тот же элемент с или если обе части умножить слева на один и тот же элемент с. Если — двусторонний идеал, то обе части сравнения можно умножить на с и справа. Отсюда, далее, следует: если , то

итак, сравнения по двустороннему идеалу можно почленно скла­дывать и умножать.

Обе части сравнения можно также умножать на обычное целое число n. В случае n = -1, если скомбинировать приведенные выше рассуждения, получается, в частности, что сравнения можно и почленно вычитать.

Следовательно, со сравнениями можно оперировать точно так же, как с равенствами. Только сокращать, вообще говоря, нельзя: в области целых чисел, например,

но сравнение неверно, хотя

Двусторонние идеалы находятся в том же отношении к поня­тию гомоморфизма колец, что и нормальные подгруппы к поня­тию гомоморфизма групп. Обратимся к понятию гомомор­физма.

Гомоморфизм определяет разбиение кольца на классы: класс будет состоять из всех элементов , имеющих один и тот же образ . Это разбиение на классы мы можем описать точнее:

Класс n кольца , который при гомоморфизме соответ­ствует нулевому элементу, является двусторонним идеалом в , а остальные классы являются классами вычетов по зтому иде­алу.

Доказательство. Сначала докажем, что n —модуль. Если а и b при гомоморфизме переходят в нуль, то в нуль переходят -b и разность а - b следовательно, вместе с а и b классу n принадлежит и разность а - b.

Далее, если а переходит в нуль и — произвольный элемент кольца, то переходит в и, следовательно, принадле­жит n. Равным образом, переходит в нуль и элемент . Следова­тельно, n — двусторонний идеал.

Элементы одного и того же класса вычетов по n, представителем которого служит а, переходят в , т. е. в , и, следовательно, принадлежат одному классу . Если, наоборот, элемент b переходит в , то b - а переходит в 0 и, сле­довательно, , т. е. b лежит в том же классе вычетов, что и а. Тем самым требуемое доказано.

Итак, каждому гомоморфизму соответствует некоторый двусто­ронний идеал, являющийся его ядром.

Обратим теперь эту связь — будем исходить из произвольного идеала m кольца и зададимся вопросом: существует ли гомо­морфный образ кольца такой, что классы вычетов по идеалу m отображаются в элементы кольца ?

Чтобы построить такое кольцо, в качестве элементов конструируемого кольца возьмем просто классы вычетов по модулю m; класс вычетов а + m обо­значим через , класс вычетов b + m — через и определим как класс, в котором лежит сумма а + b, и как класс, в котором лежит произведение ab. Если — какой-нибудь другой элемент из , а — другой элемент из , то в соот­ветствии со сказанным выше

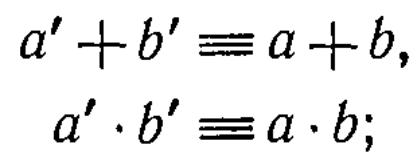
следовательно, лежит в том же классе вычетов, что и ; точно так же лежит в том же классе вычетов, что и . Таким образом, наше определение суммы и произведения классов не зависит от выбора элементов а, b в классах .

Каждому элементу а соответствует класс вычетов , и это отображение гомоморфно, потому что сумма а+b переходит в сумму , а произведение ab - в произведение .

Следова­тельно, классы вычетов образуют некоторое кольцо (§ 12). Это кольцо мы назовем кольцом классов вычетов или фактор-кольцом кольца по идеалу m или кольца по модулю m. С по­ мощью указанного выше соответствия кольцо о гомоморфно ото­бражается на кольцо . В этой ситуации идеал m играет ту же роль, что раньше играл n.

Здесь мы видим принципиальную важность двусторонних идеалов: они позволяют строить кольца, гомоморфные данному кольцу. Элементами такого нового кольца являются классы вы­четов по некоторому двустороннему идеалу. Любые два класса вычетов складываются и умножаются, потому что можно склады­вать и умножать два произвольных представителя этих классов. Из следует, что ; таким образом, сравнения при пере­ходе к классам вычетов становятся равенствами, и операции над сравнениями в кольце соответствуют операциям над равенствами в кольце .

Построенные здесь кольца частного вида, гомоморфные дан­ному кольцу , — кольца классов вычетов — исчерпывают, по существу, все кольца, гомоморфные кольцу . Действительно, если — произвольное кольцо, гомоморфное кольцу , то мы уже видели, что элементы из взаимно однозначно соответствуют классам вычетов по некоторому двустороннему идеалу n в . Класс вычетов соответствует элементу Сумма и про­изведение двух классов вычетов переходят соответственно в и, следовательно, им соответствуют элементы

и

Таким образом, сопоставление классам вычетов элементов из является изоморфизмом. Мы доказали следующее утверждение:

Каждое кольцо , гомоморфное кольцу , изоморфно некоторому кольцу классов вычетов . При этом n является двусторонним идеалом, элементы которого имеют нулевой образ в . Обратно, любое кольцо классов вычетов является гомоморфным образом кольца (теорема о гомоморфизмах колец).