Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

ГОУ ВПО Нижегородский государственный педагогически университет им.К.Минина

Факультет математики, информатики и физики

Кафедра алгебры и геометрии

Кольца, тела, поля.

Курсовая работа

студента группы МИ-10

Коржавин М. С.

Научный руководитель:

Глуздов В.А.

Нижний Новгород

2014

Оглавление

Оглавление____________________________________________________________2

Кольца________________________________________________________________4

Гомоморфизмы и изоморфизмы___________________________________________8

Построение частных_____________________________________________________9

Кольца многочленов____________________________________________________11

Примеры______________________________________________________________18

Выводы_______________________________________________________________20

Список используемой литературы_________________________________________21

Введение:

{Формулировка введения не до конца обдумана}

Кольца

Алгебра и арифметика оперируют объектами различной при­роды; это — целые, рациональные, вещественные, комплексные, алгебраические числа, многочлены или рациональные функции от n переменных и т. д.

Под системой с двойной композицией подразумевается про­извольное множество элементов а, b, ..., в котором для любых двух элементов а, b однозначно определены сумма а+b и про­изведение а*b, вновь принадлежащие данному множеству.

Система с двойной композицией называется кольцом, если операции над элементами этой системы подчиняются следующим законам:

I Законы сложения:

а) Закон ассоциативности: а + (b + с) = (а + b) + с.

б) Закон коммутативности: a + b = b+a.

в) Разрешимость уравнения а+х = b для всех а, Ь.

(Однозначная разрешимость не требуется, а получается дальше как следствие.)

II Закон умножения:

а) Закон ассоциативности: а*bc = ab*с.

III Законы дистрибутивности:

а) а * (b + с) = ab + ас;

б) (b+с)*а = bа + са.

Примечание. Если для умножения выполняется закон коммутативности:

II б), ab — b-a,то кольцо называется коммутативным.

К законам сложения. Три закона I а), б), в) означают в со­вокупности, что элементы кольца образуют абелеву группу относительно сложения (Эту группу называют аддитивной группой кольца). Таким образом, мы можем перенести на кольца теоремы абелевых групп: су­ществует один и только один нулевой элемент 0 со свойством

а+0 = а для всех а.

Далее, для каждого элемента а существует противоположный элемент -а со свойством

(-а) + а = 0.

Таким образом, уравнение а+х = b не только разрешимо, но и однозначно разрешимо; его единственное решение — элемент

х = (- а) + b,

который мы обозначаем также и через b-а. Так как

а-b = а+(-b),

любая разность может быть превращена в сумму, следовательно, в этом смысле для разностей имеют место те же правила пере­становки, что и для сумм, например,

(а-b)-с = (а-с)-b.

-(-а) = а и а - а = 0.

К законам ассоциативности. На основе закона ассоциативности для умножения можно опреде­лить сложные произведения

и доказать их основное свойство:

Точно так же можно определить суммы

и доказать их основное свойство:

В силу I 6) в любой сумме можно произвольным образом пере­ставлять слагаемые, а в коммутативных кольцах то же самое верно и для произведений.

К законам дистрибутивности. Если имеет место закон коммута­тивности для умножения, то, конечно, закон III 6) является следствием закона III а).

Из III а) с помощью индукции по n получаем

и, равным образом, из III 6):

Оба эти закона дают привычное правило для перемножения сумм:

Законы дистрибутивности выполняются также и для вычита­ния; например,

в чем легко убедиться непосредственно:

В частности,

или: произведение равно нулю, когда равен нулю один из сомно­жителей.

Обращение этого предложения, не обязательно верно: может случиться так, что

В этом случае элементы а и b называют делителями нуля, при­чем а - левым делителем нуля, а b - правым делителем нуля. (В коммутативных кольцах оба эти понятия совпадают.) Оказы­вается удобным и сам нуль считать делителем нуля. Поэтому элемент а называется левым делителем нуля, если существует такой элемент , что (Предполагается, что в кольце есть элементы, отличные от нуля)

Если в кольце нет делителей нуля, отличных от самого нуля, т. е. если из ab = 0 следует, что или а = 0, или b = 0, то гово­рят о кольце без делителей нуля. Если, кроме того, кольцо комму­тативно, то оно называется целостным.

Примеры. Все указанные ранее кольца (кольцо целых чисел, кольцо рациональных чисел и т. д.) являются примерами колец без делителей нуля. Кольцо непрерывных функций на интервале (—1, 1) обладает делителями нуля, потому что если положить

то окажется, что

Пары целых чисел (а₁а₂) с операциями

образуют кольцо с делителями нуля.

Равенство ах=ay можно сокращать на а, если а не являет­ся левым делителем нуля. (В частности, в целостном кольце можно сокращать на любой элемент )

Задача. Построить, исходя из произвольной абелевой группы, кольцо, аддитивная группа которого есть данная группа, а умножение таково, что произведение любых двух элементов равно нулю.

Единичный элемент. Если кольцо обладает левым единичным элементом е:

и одновременно — правым единичным элементом е'

то оба эти элемента должны быть равны, так как

Точно так же любой правый единичный элемент равен е и левый единичный элемент тоже. При этих условиях элемент е называют просто единичным элементом или единицей и говорят о кольце с единичным элементом или о кольце с единицей. Часто единич­ный элемент обозначают символом 1, если это не приводит к путанице с числом 1.

Целые числа образуют кольцо с единицей, а четные числа — кольцо без единицы. Существуют также кольца, в которых есть несколько правых единичных элементов, но ни одного левого или наоборот.

Обратный элемент. Если а — произвольный элемент кольца с единицей е, то под левым обратным элементом к а подразуме­вается элемент со свойством

а под правым обратным — элемент со свойством

Если элемент а обладает левым обратным и правым обратным элементами, то последние опять совпадают, так как

и, следовательно, каждый правый обратный, как и каждый левый обратный для элемента а равны указанному выше элементу. В этом случае говорят: элемент а обладает обратным элементом, а сам обратный элемент обозначают через .

Степени и кратные. На основе закона ассоциативности для каждого элемента а в кольце можно определить степени аⁿ (n — натуральное число) и получить обыч­ные правила действий:

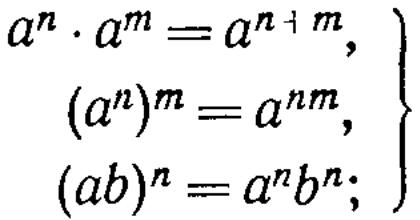
при этом последнее равенство справедливо для коммутативных колец.

Если кольцо обладает единицей, а элемент а — обратным, то можно ввести нулевую и отрицательные степени, при этом равенства (1) остаются верными.

Точно так же в аддитивной группе можно ввести кратные

тогда:

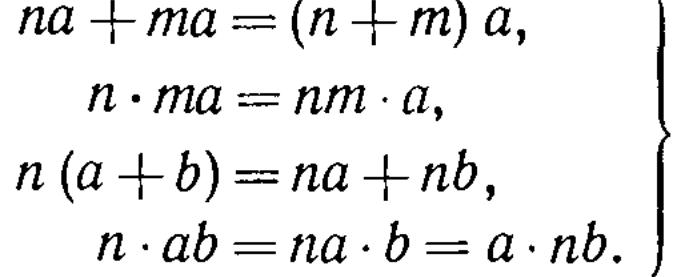
Как и в случае степеней, положим

тогда равенства (2) окажутся выполненными для всех целых n и m (положительных, отрицательных и нуля).

Вместе с тем выражение n * а не следует рассматривать как настоящее произведение двух элементов кольца, потому что n в общем случае не является элементом кольца, а представляет собой нечто внешнее: целое число. Если, однако, кольцо обладает единицей е, то nа можно рассматривать как настоящее произве­дение, а именно:

теорема о биноме:

где - целое число

Задача. Если элементы а и b перестановочны, т. е. ab = ba, то а пере­становочен с — b, nb и b^-1. Если а перестановочен с b и с, то он перестано­вочен с b+с и bс.

Тело. Кольцо называется телом, если:

а) в нем есть по крайней мере один элемент, отличный от нуля:

б) уравнения

при разрешимы.

Если, кроме того, кольцо коммутативно, то оно называется полем или рациональным кольцом.

Доказывается, что из а) и б) следует

в) существование левой единицы е. Действительно, для каж­дого уравнение ха = а разрешимо; обозначим его решение через е. Для произвольного b уравнение ах = b разрешимо; сле­довательно,

Точно так же устанавливается существование правой единицы и вообще единичного элемента.

Из в) следует непосредственно

г) существование левого обратного а^-1 для каждого и, равным образом, правого обратного; итак, установлено существо­вание обратного элемента вообще.

Так же как в случае групп, далее докажем, что, наобо­рот, из в) и г) следует б).

Задача. Провести доказательство.

В теле нет делителей нуля, потому что из ab = 0, с помощью умножения на а^-1 следует равенство b = 0.

Уравнения (3) разрешимы однозначно, потому что из сущест­вования двух решений х, х', скажем, первого уравнения следо­вало бы, что

ах = ах'

и с помощью умножения на а^-1 слева

х = х'.

Решения уравнений (3), естественно, равны

В коммутативном случае , поэтому пишут также b/а.

Отличные от нуля элементы произвольного тела составляют относительно операции умножения группу — мультипликативную группу тела.

Таким образом, тело объединяет в себе сразу две группы: мультипликативную и аддитивную. Обе они связаны дистрибутив­ными законами.

Примеры.

1. Рациональные числа, вещественные числа, комплексные числа образуют поля.

2. Поле из двух элементов 0 и 1 строится следующим образом: эти элементы перемножаются, как числа 0 и 1. Относительно сложения элемент 0 является нулевым элементом:

0 + 0 = 0; 0 + 1=1; 1+0 = 1;

пусть далее 1 + 1=0. Правило сложения то же, что и в компо­зиции циклической группы с двумя элементами; тем самым выполнены законы сложения. Законы умножения также выпол­нены, потому что они выполняются для обычных чисел 0 и 1. Первый закон дистрибутивности доказывается перебором всех воз­можностей: если в требуемое равенство входит нуль, то все три­виально, так что остается рассмотреть лишь случай

который приводит к справедливому равенству 0 = 0. Наконец, уравнение 1* х = а разрешимо при каждом а: решением служит х = а.

Гомоморфизмы и изоморфизмы

Пусть — системы с двойной композицией. Согласно общему определению, отображение из называется гомоморфизмом, если соотношения а+b=с и ab = d при этом отображении сохраняются, т. е. если сумма а + b переходит в сумму , а произведение a*b — в произведение . Множество , являющееся в образом множества , называется в этом слу­чае гомоморфным образом множества . Если отображение взаимно однозначно, то отображение называют изоморфизмом в соответствии с нашим общим определением и пишут Отношение рефлексивно и транзитивно, а так как отображение, обратное к изо­морфизму, является изоморфизмом, это отношение и симметрично.

Гомоморфный образ кольца является кольцом.

Доказательство. Пусть — кольцо, —система с двой­ной композицией, а — гомоморфное отображение из на . Мы должны показать, что —снова кольцо. Как и в случае групп, доказательство проводится следующим образом.

Пусть — любые три элемента из ; докажем какое-либо из правил вычисления, например, , для чего фиксируем прообразы а, b, с элементов . Так как — кольцо, выполняется равенство а (b + с) = ab + ас, а в силу гомоморфности отображения . Точно так же прово­дится доказательство всех законов ассоциативности, коммутатив­ности и дистрибутивности. Для доказательства разрешимости урав­нения нужно найти прообразы а, b и решить уравнение а+х = b, откуда в силу гомоморфности получится, что .

Нулю и противоположному элементу —а элемента а соответ­ствуют при гомоморфизме нуль и противоположный элемент из кольца . Если обладает единицей, то ей соответствует еди­ничный элемент в .

Доказательство такое же, как в случае групп.

Если кольцо коммутативно, то коммутативно и .

Если — целостное кольцо, то не обязано быть целостным;

кольцо может быть целостным и тогда, когда таковым не является. Но если отображение изоморфно, то, конечно, все алгебраические свойства кольца переносятся на кольцо . Отсюда следует утверждение:

Изоморфный образ целостного кольца (соответственно поля) является целостным кольцом (соответственно полем).

Здесь уместно сформулировать одну почти тривиальную тео­рему, которая будет важна:

Пусть и — два кольца, не имеющие общих элементов; пусть содержит подкольцо изоморфное . Тогда существует кольцо содержащее .

Доказательство. Удалим из элементы кольца и заменим их на соответствующие при изоморфизме элементы кольца . Суммы и произведения на замененных и оставшихся элементах определим так, как это получается при изоморфном соответствии для исходных элементов в (Например, если перед заменой элементов выполнялось равенство , затем а' заменялся на а, а b' и с' оставались неизменными, то мы пола­гаем ab'=c'.) Таким способом из возникает кольцо , которое и в самом деле содержит .

Построение частных

Если коммутативное кольцо вложено в некоторое тело , то внутри из элементов кольца можно строить частные (из ab=ba следует, что , если слева и справа умножить на )

Для них имеют место следующие правила:

тогда и только тогда, когда

Для доказательства нужно убедиться в том, что обе части после умножения на bd дают одно и то же и что из bdx = bdy следует х = у.

Таким образом, мы видим, что частные а/b составляют неко­торое поле , которое называется полем частных коммутативного кольца . Далее, из правил (1) усматривается, что способ, кото­рым дроби сравниваются, складываются, умножаются, оказывается известным, как только эти операции определяются над элементами кольца , т. е. строение поля частных полностью определяется строением кольца , или: поля частных изоморфных колец изо­морфны. В частности, любые два поля частных одного и того же кольца обязательно изоморфны, или: поле частных определяется кольцом 34 однозначно с точностью до изоморфизма, если только вообще данное кольцо обладает полем частных.

Зададимся теперь вопросом: какие коммутативные кольца обладают полями частных? Или, что то же самое, — какие ком­мутативные кольца могут быть погружены в поля?

Для того чтобы кольцо можно было погрузить в тело, необходимо прежде всего, чтобы в не было делителей нуля, потому что в теле делителей нуля нет. В коммутативном случае это условие и достаточно: каждое целостное кольцо можно по­грузить в некоторое поле (Для некоммутативных колец без делителей нуля эта теорема неверна. Соответствующий пример был впервые построен Мальцевым А- И. (Math. Ann., 1936, 113, S. 686-691) )

Доказательство. Мы можем исключить тривиальный слу­чай, когда состоит только из нулевого элемента. Рассмотрим множество всех пар элементов (а, Ь), где . Этим парам позднее мы сопоставим дроби а/b.

Положим , если ad = bc. (Ср. приведенные выше формулы (1).) Определенное таким образом отношение ~ является, очевидно, рефлексивным и симметричным; кроме того, оно и транзитивно, потому что из

следует, что

и поэтому

Таким образом, в силу и коммутативности кольца :

Отношение ~ обладает, таким образом, всеми свойствами экви­валентности. Эта последняя опреде­ляет некоторое разбиение пар (а, b) на классы, при котором эквивалентные пары попадают в один класс. Класс, которому при­надлежит пара (а, b), будет обозначаться символом а/b. Как следствие этого определения равенство a/b = c/d оказывается выполненным тогда и только тогда, когда т. е. когда ad = be.

В соответствии с предыдущими формулами (1) мы определим сумму и произведение новых символов а/b равенствами

и

Эти определения корректны, потому что, во-первых, если

и , то и выражения имеют смысл;

во-вторых, праьы; части не зависят от выбора представителей (а, b) и (с, d) классов а/b и c/d. Действительно, заменим в (2) а и b на а' и b', где

ab' —bа';

тогда

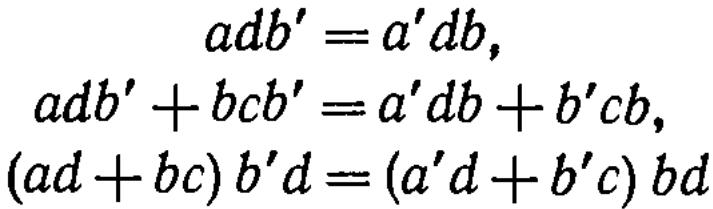
и, следовательно,

Точно так же:

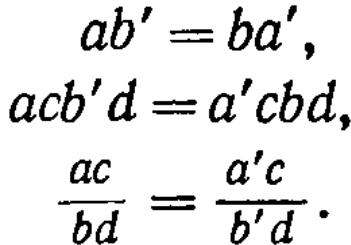
Соответствующие равенства получаются при замене (с, d) на (с', d’), где cd' = dc'.

Без труда показывается, что полученная конструкция обла­дает всеми свойствами поля. Например, закон ассоциативности сложения получается так:

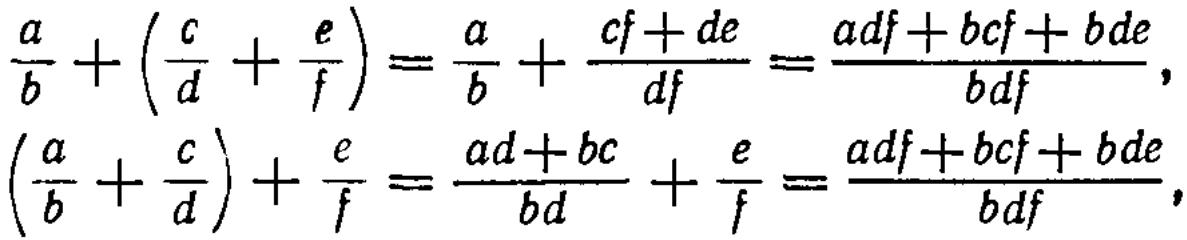
а остальные законы аналогично.

Чтобы установить, что построенное поле содержит кольцо , мы должны отождествить элементы из с некоторыми дробями. Делается это так.

Сопоставим элементу с все дроби , где . Эти дроби равны между собой:

так как

Следовательно, каждому элементу с сопоставляется лишь одна дробь. При этом различным элементам с, с' сопоставляются раз­личные дроби, потому что из

следует, что

или, так как , можно осуществить сокращение:

Итак, элементам кольца взаимно однозначным образом сопо­ставлены совершенно определенные дроби.

Если или в кольце , то для произвольных это означает, что

соответственно

Следовательно, дроби складываются и умножаются так же,

как элементы кольца ; поэтому они составляют систему, изо­морфную кольцу . В силу сказанного мы можем заменить дроби на соответствующие им элементы с. Тем самым

мы получаем требуемый результат: построенное поле содержит кольцо

Мы доказали, следовательно, существование поля, содержа­щего заданное целостное кольцо .

Построение частных является первым средством построения из данных колец других колец (в данном случае — полей). На­пример, именно так из кольца обычных целых чисел строится поле ( рациональных чисел.