
- •Ковалев а.Н. Эконометрика
- •Ковалев а.Н. Эконометрика
- •Методические рекомендации для проведения лабораторных занятий и самостоятельной работы студентов по курсу «Эконометрика» предназначено для студентов всех специальностей и направлений подготовки вуза.
- •Содержание
- •Введение
- •Тема 1. Предмет, метод и задачи эконометрики
- •Контрольные вопросы
- •Тема 2. Парная регрессия и корреляция
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Задача 6. В результате наблюдения 16 пар переменных (х и y) получены следующие данные:
- •Тема 3. Множественная регрессия и корреляция
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Тема 4. Нелинейные регрессионные модели
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Тема 5. Регрессионные модели с переменной структурой
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Контрольные вопросы
- •Задания для лабораторных занятий и самостоятельного решения
- •Тема 7. Системы одновременных уравнений
- •Контрольные вопросы
- •Задания для практических занятий и самостоятельного решения
- •Глоссарий
- •Словарь терминов
- •Примерная тематика рефератов
- •Список литературы
- •Ковалев Александр Николаевич Эконометрика
- •308023, Г. Белгород, ул. Садовая, 116а
Тема 4. Нелинейные регрессионные модели
Основными направлениями изучения данной темы является рассмотрение нелинейных зависимостей, линеаризации регрессионных моделей, производственных функций.
Изучив данную тему студент должен знать:
–- виды нелинейных зависимостей;
– подходы к линеаризации регрессионных моделей;
– производственные функции и их анализ.
Контрольные вопросы
Какие классы нелинейных регрессий Вы знаете?
По каким признакам классифицируются методы оценки параметров нелинейных моделей?
Каким образом линеаризуются нелинейные модели?
Каковы причины нелинеаризуемости моделей?
Охарактеризуйте производственную функцию Кобба–Дугласа с постоянной эластичностью замещения
Что такое «предельная норма замещения»?
Задания для лабораторных занятий и самостоятельного решения
Задача 1. На основании данных о cреднемесячном обороте розничной торговле на душу населения (у) и среднедушевых денежных доходах населения по субъектам РФ (х), за последний год, представленных на официальном сайте Федеральной службы государственной статистики России (www.gks.ru), расчитайте параметры следующих функций (задание выполняется по вариантам, т.е. по федеральным округам):.
линейной;
степенной;
показательной;
праболы;
равносторонней гиперболы.
Оцените каждую модель через коэффициент детерминации, среднюю ошибку аппроксимации и F - критерий Фишера.
Задача 2. На основании данных о ВРП регионов Российской Федерации (у), среднегодовой полной учетной стоимости основных фондов по субъектам РФ (х1), численность занятых в экономике соответствующего региона (х2) за последний год, представленных на официальном сайте Федеральной службы государственной статистики России (www.gks.ru), расчитайте параметры функции Кобба-Дугласа и дайте им экономическое обоснование (задание выполняется по вариантам, т.е. по федеральным округам).
Задача 3. Имеются данные о доходах и потреблении в регионе за 2002-2011 гг., млн. руб. Постройте уравнения регрессии вида и y = axb. Проведите дисперсионный анализ полученных результатов.
Годы |
Доход |
Потребление |
2002 |
751 |
672 |
2003 |
779 |
696 |
2004 |
810 |
737 |
2005 |
864 |
767 |
2006 |
857 |
762 |
2007 |
874 |
779 |
2008 |
906 |
823 |
2009 |
942 |
864 |
2010 |
988 |
903 |
2011 |
1015 |
927 |
Задача 4. Взаимосвязь между производительностью труда и стажем полученная в результате наблюдения 48 рабочих характеризуется следующим уравнением:
УХ = 53Х0,5
при: ![]()
![]()
Определите коэффициент эластичности.
Задача 5. Зависимость между объемом выпуска продукции и затратами труда и капитала характеризуются следующей функцией Кобба–Дугласа:
V = 1,89 К0,33 L0,67
Как изменится объем выпуска продукции при увеличении затрат капитала на 7,1% и снижении числа работников на 3,2%.
Задача 6. Зависимость спроса на свинину У от цены на неё Х1 и от цены на говядину Х2 представлена уравнением:
![]()
Необходимо:
Представить данное уравнение в естественной форме (не в логарифмах), т.е. потенцировать его обе части .
Оценить значимость параметров данного уравнения, если известно, что t–критерий для параметра а1 при Х1 составил 0,856, а для параметра а2 при Х2 составил 1,025.
Тесты
1. Коэффициент корреляции для модели парной нелинейной регрессии рассчитывается по формуле:
а)
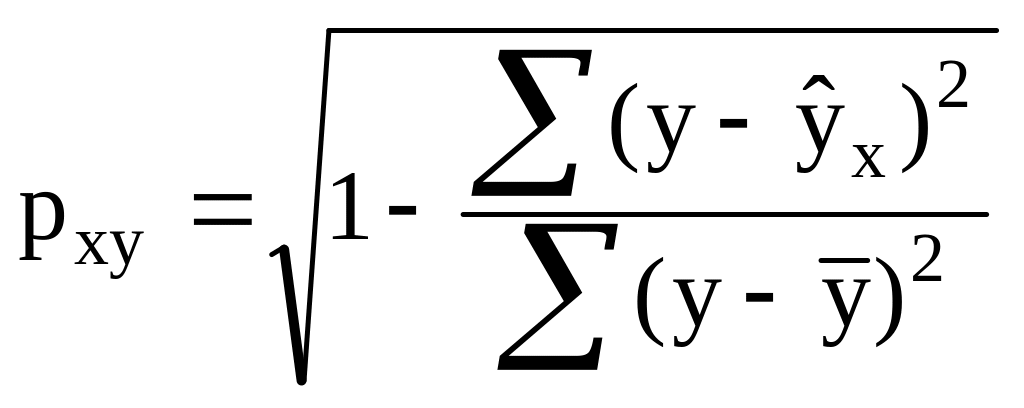 ;
;
б)
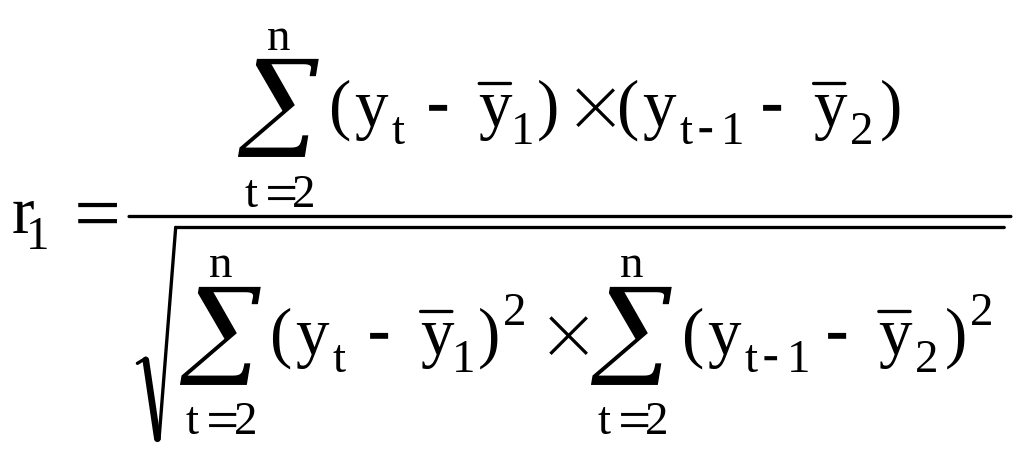 ;
;
в)
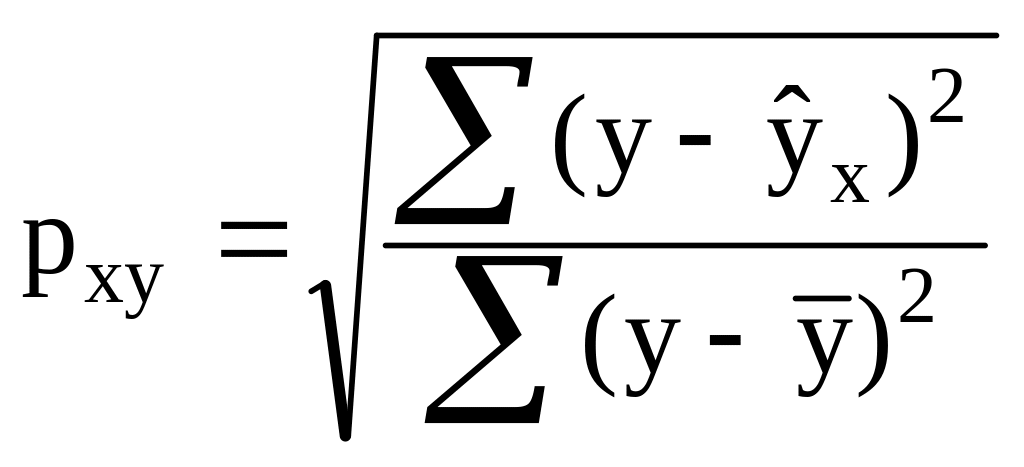 ;
;
г) .
2. Регрессионная модель в форме равносторонней гиперболы является:
а) регрессионной моделью, линейной по переменной;
б) регрессионной моделью, линейной по объясняющим параметрам;
в) регрессионной моделью, нелинейной по переменной;
г) регрессионной моделью, нелинейной по объясняющим параметрам.
3.
Коэффициент эластичности для функции
![]() равен:
равен:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
4. Степенная регрессионная модель является:
а) регрессионной моделью, линейной по переменной;
б) регрессионной моделью, линейной по объясняющим параметрам;
в) регрессионной моделью, нелинейной по переменной;
г) регрессионной моделью, нелинейной по объясняющим параметрам.
5.
Коэффициент эластичности для функции
![]() равен:
равен:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
6. Экспоненциальная регрессионная модель является:
а) регрессионной моделью, линейной по переменной;
б) регрессионной моделью, линейной по объясняющим параметрам;
в) регрессионной моделью, нелинейной по переменной;
г) регрессионной моделью, нелинейной по объясняющим параметрам.
7.
Коэффициент эластичности для функции
![]() равен:
равен:
а)
![]() ;
;
б) ;
в)
![]() ;
;
г)
![]() ;
;
8. Показательная регрессионная модель является:
а) регрессионной моделью, линейной по переменной;
б) регрессионной моделью, линейной по объясняющим параметрам;
в) регрессионной моделью, нелинейной по переменной;
г) регрессионной моделью, нелинейной по объясняющим параметрам.
9. Полиномиальная регрессионная модель является:
а) регрессионной моделью, линейной по переменной;
б) регрессионной моделью, линейной по объясняющим параметрам;
в) регрессионной моделью, нелинейной по переменной;
г) регрессионной моделью, нелинейной по объясняющим параметрам.
