Тема 3. Множественная регрессия и корреляция

При изучении данной темы необходимо уяснить понятие множественной регрессии, изучить линейную модель множественной регрессии, метод наименьших квадратов, определить параметры уравнения множественной регрессии, показатели качества регрессии, линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками, проблему мультиколлинеарности.

Изучив данную тему студент должен знать:

– понятие множественной регрессии;

– классическую линейную модель множественной регрессии;

– расчет параметров уравнения множественной регрессии и метод наименьших квадратов;

– множественный коэффициент корреляции и множественный коэффициент детерминации;

– линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками;

– мультиколлинеарность и методы её устранения.

Контрольные вопросы

1. Что показывают коэффициенты множественной корреляции и детерминации?

2. Какие гипотезы проверяют с помощью критерия Фишера?

3. Приведите формулы расчета оценок коэффициентов множественной линейной регрессии по МНК.

4. Какими свойствами обладают МНК–оценки классической линейной эконометрической модели?

5. Перечислите свойства фактической ошибки эконометрической модели.

6. Каким образом проверяется наличие автокорреляции ошибок модели?

7. Каковы последствия мультиколинеарности факторов?

8. Что такое «ложная корреляция»?

Задания для лабораторных занятий и самостоятельного решения

Задача 1. На основании данных о среднемесячном обороте розничной торговле на душу населения (у), среднедушевых денежных доходах населения по субъектам РФ (х1) и численностью населения (х2), за последний год, представленных на официальном сайте Федеральной службы государственной статистики России (www.gks.ru), исследуйте зависимость между вышеуказанными переменными, построив уравнение множественной регрессии и дав интерпретацию его параметров. Задание выполняется по вариантам, т.е. по федеральным округам. Также рассчитайте:

• коэффициенты множественной корреляции и детерминации;

• парные и частные коэффициенты корреляции;

• скорректированный коэффициент множественной детерминации;

• F-критерий Фишера;

• среднюю ошибку аппроксимации.

• включите в данную модель еще 2-3 фактора и определите имеет ли место мультиколлинеарности в полученном уравнении регрессии.

Дайте интерпретацию полученным результатам.

Задача 2. При исследовании факторов, влияющие на академическую успеваемость студентов, получена следующая эконометрическая модель:

У_Х = 1,05 + 1,58Х₁ + 0.58Х₂

n = 150 R² = 0,35

где

У_Х -оценка, полученная студентом на экзамене;

Х₁ - доля лекций, посещенных данным студентом;

Х₂-доля выполненных им домашних заданий.

Дайте интерпретацию коэффициентам регрессии.

Согласуются ли знаки коэффициентов с Вашими ожиданиями.

Предположим, что лекции занимают 25 часов, а выполнение всех домашних заданий – 50 часов. Если у студента появился лишний час, который он может посвятить учебе, следует ли ему с целью повышения будущей оценки пойти на лекцию, или лучше остаться дома и заниматься домашними заданиями.

Как бы изменились ваши рекомендации, если бы структура курса была иной: 50 часов лекций и 10 часов на выполнение домашних заданий.

Как вы интерпретируете значение R² = 0,35.

Задача 3. Имеются данные о 20 крупнейших по размеру активов российских банках.

Изучите влияние величины активов и собственных средств на величину балансовой прибыли банка.

Место по активам	Банк	Активы (тыс. руб.)	Собственный капитал (тыс. руб.)	Балансовая прибыль (тыс. руб.)
1	Сбербанк России	859 389 961	103 158 215	10 193 908
2	Внешторгбанк	151 434 783	54 819 440	6 811 611
3	Альфа-банк	113 485 535	23 575 900	336 921
4	Газпромбанк	109 307 948	24 229 687	707 940
5	Международный промышленный банк	108 523 559	28 031 236	101 800
6	Международный московский банк	83 527 023	3 162 286	336 459
7	Росбанк	70 114 866	8 840 582	237 329
8	Банк Москвы	66 404 075	4 233 569	267 031
9	МДМ-банк	47 189 348	5 223 902	3 552
10	Сургутнефтегазбанк	45 329 343	1 284 655	40 180
11	Доверительный и инвестиционный банк	44 339 783	4 255 064	288 406
12	Ситибанк	43 769 237	5 415 056	615 682
13	Промышленно-строительный банк	37 008 645	3 019 428	353 796
14	"Менатеп Санкт-Петербург"	29 002 604	2 315 349	151 925
15	"Уралсиб"	27 782 862	6 718 455	192 945
16	Райффайзенбанк Австрия	25 069 302	2 127 745	406 643
17	БИН-банк	22 425 691	3 372 372	41 599
18	"Петрокоммерц"	22 096 880	5 538 419	308 164
19	"Еврофинанс"	19 959 242	3 323 362	765 762
20	Номос-банк	19 596 150	4 074 932	14 033

Задача 4. Имеются данные о размерах накопления, доходов и стоимости имущества домашних хозяйств:

(тыс. руб.)

Годы	1	2	3	4	5	6	7
Доходы,	6,0	8,3	6,8	4,5	4,5	9,0	7,5
Стоимость имущества	90	60	60	23	135	45	45
Накопления	0,3	1,1	0,8	0,6	0,3	1,1	0,9

Исследуйте зависимость между размером накопления, величиной доходов и стоимостью имущества, построив уравнение множественной регрессии и дав интерпретацию его параметров.

Задача 5. Зависимость расходов на продукты питания по совокупности семей характеризуется следующим уравнением:

y_x = 0,6 + 0,35x₁ + 730x₂,

где у_х – расходы семьи на продукты питания за месяц;

х₁ – месячный доход на одного члена семьи;

х₂ – размер семьи.

Дайте интерпретацию полученных коэффициентов.

Задача 6. Оцените статистическую значимость коэффициента а₁ если его значение полученное в результате 22 наблюдений равно -645,7, при остаточной дисперсии равной 59 и общей дисперсии равной 234.

Задача 7. Рассчитайте множественный коэффициент корреляции между кредитоспособностью клиента, объемом его деятельности и стоимостью имущества если остаточная дисперсия равна 237, а общая дисперсия 678.

Задача 8. Для изучения влияния стоимости основных и оборотных средств на величину валового дохода было исследовано 12 торговых предприятий и получены следующие данные:

Номер предприятия	Валовой доход за год, млн.руб.	Среднегодовая стоимость, млн.руб.
		основных фондов	оборотных средств
1	244	142	126
2	76	34	67
3	54	20	65
4	136	60	76
5	145	67	34
6	106	122	60
7	132	139	65
8	67	149	50
9	96	137	43
10	284	185	127
11	192	138	106
12	90	118	55

Необходимо:

1. Построитель линейное уравнение множественной регрессии и экономически интерпретировать его параметры.

2. Рассчитать частные коэффициенты эластичности.

3. Определить стандартизированные коэффициенты регрессии.

4. Сделать вывод о тесноте связи результата и факторов.

5. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции. Сделайте вывод.

6. Дайте оценку полученного уравнения на основе коэффициента детерминации и общего F–критерия Фишера.

Задача 9. Имеются следующие данные:

(млрд. руб.)

Годы	ВВП	M2
1	1359	861
2	1472	908
3	1598	1023
4	1782	1163
5	1990	1286
6	2249	1389
7	2508	1500
8	2723	1633
9	3052	1795
10	3166	1954

Оцените гомоскедастичность остатков уравнения регрессии ВВП по М2 используя тест Гольдфельда–Квандта.

Тесты

1. Среднее значение коэффициента эластичности результативного фактора в модели множественной регрессии рассчитывается по формуле:

а) ; б) ;

в) ; г) .

2. Индекс множественной корреляции в модели множественной регрессии рассчитывается по формуле:

а) 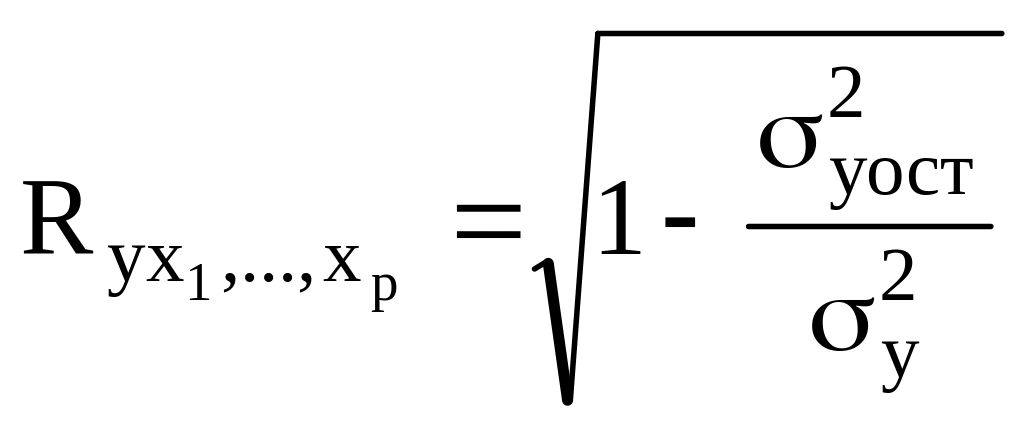; б) ;

в) ; г) .

3. Множественная регрессия – это:

а) уравнение связи с одной объясняющей переменной;

б) уравнение связи с несколькими независимыми переменными;

в) уравнение связи с несколькими зависимыми переменными;

г) уравнение связи с отсутствующими независимыми переменными.

4. Скорректированный индекс множественной детерминации в модели множественной регрессии рассчитывается по формуле:

а) ; б) ;

в) 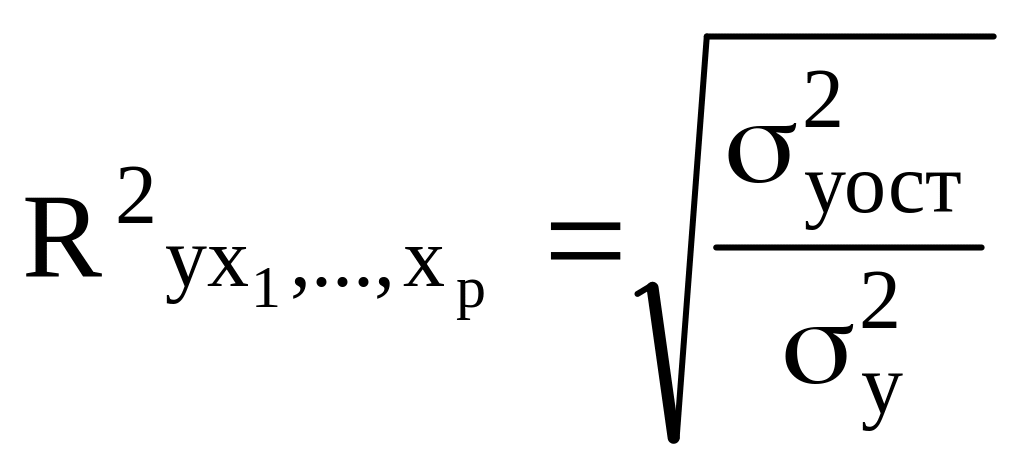; г) .

5. Для оценки мультиколлениарности факторов используют:

а) коэффициент множественной детерминации;

б) метод Гольдфельда-Кванта;

в) индекс множественной корреляции;

г) F-критерий Фишера.

6. Значение F-критерия Фишера в модели множественной регрессии рассчитывается по формуле:

а) ;

б) ;

в) ;

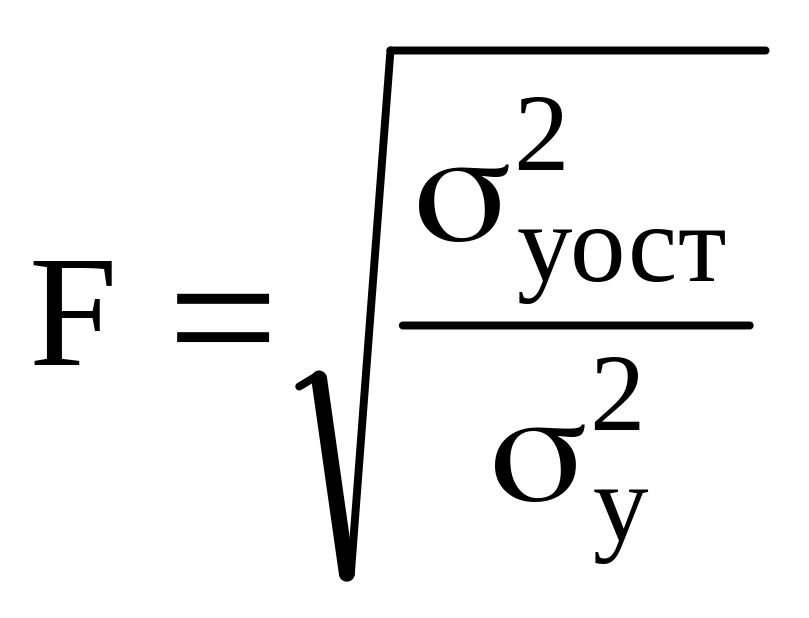г) .

7. Гомоскедастичность означает:

а) для каждого значения фактора остатки имеют одинаковую дисперсию;

б) для каждого значения фактора остатки имеют разную дисперсию;

в) для каждого значения фактора остатки имеют нулевую дисперсию;

г) для каждого значения фактора имеются нулевые остатки.

8. Значение частного F-критерия Фишера в модели множественной регрессии рассчитывается по формуле:

а) ;

б) ;

в) ;

г) .

9. Для оценки гомоскедастичности факторов используют:

а) коэффициент множественной детерминации;

б) метод Гольдфельда-Кванта;

в) индекс множественной корреляции;

г) F-критерий Фишера.

10. Средняя ошибка коэффициента уравнения множественной регрессии рассчитывается по формуле:

а) ;

б) ;

в) ;

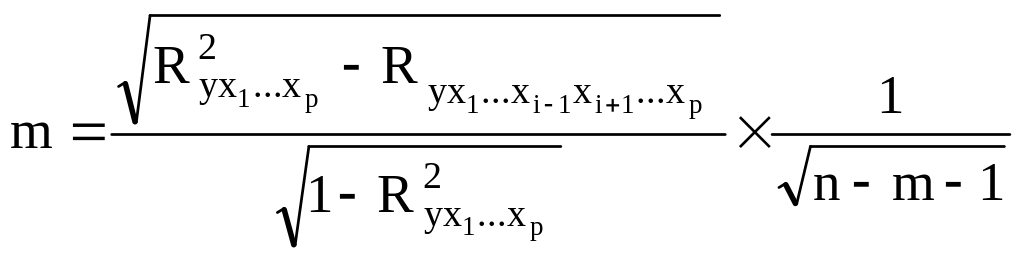г) .

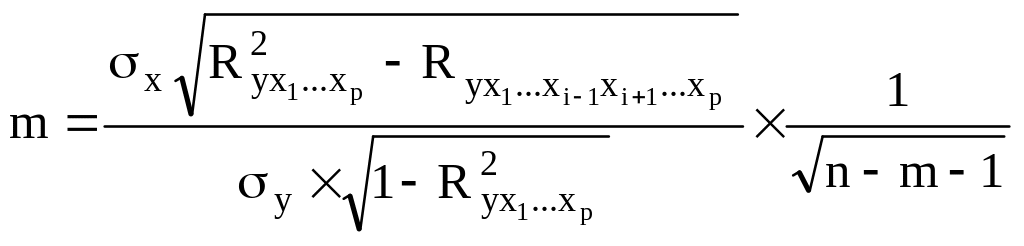11. Оценка статистической значимости присутствия каждого из факторов в модели проводится с помощью:

а) t-критерия Стьюдента;

б) частного F-критерия Фишера;

в) F-критерия Фишера;

г) критерия Дарбина-Уотсона.

12. Значение t-критерия Стьюдента для коэффициента уравнения множественной регрессии рассчитывается по формуле:

а) ;

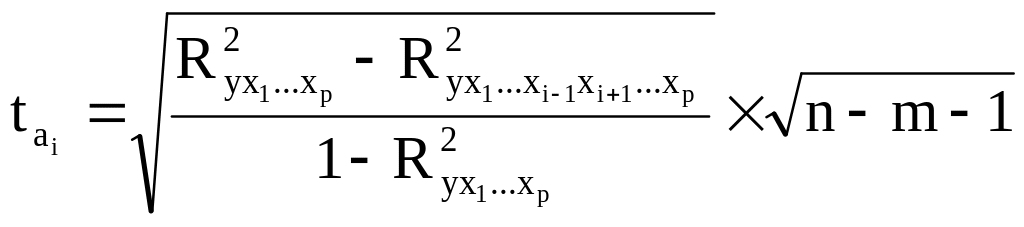б) ;

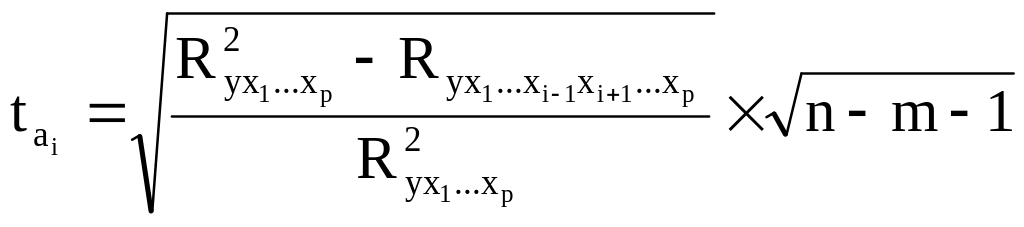в) ;

г) .

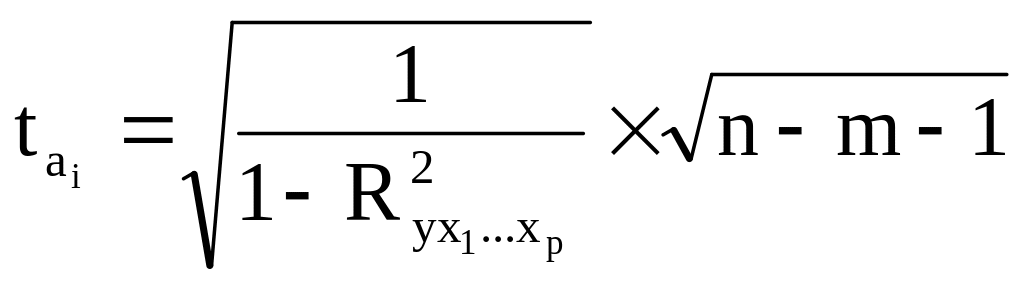13. Оценка значимости коэффициентов множественной регрессии проводиться с помощью:

а) t-критерия Стьюдента;

б) F-критерия Фишера;

в) критерия Энгеля-Грангера;

г) критерия Дарбина-Уотсона.

14. Значение коэффициента уравнения множественной регрессии рассчитывается по формуле:

а) ;

б) ;

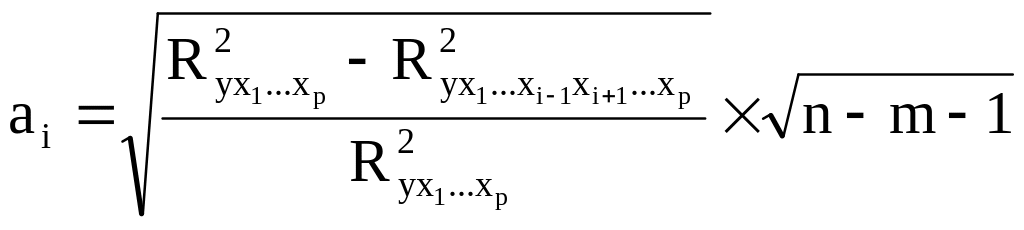в) ;

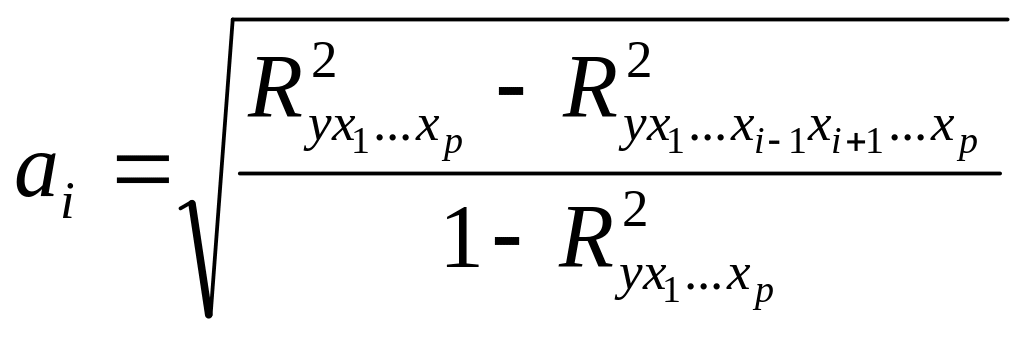г) .

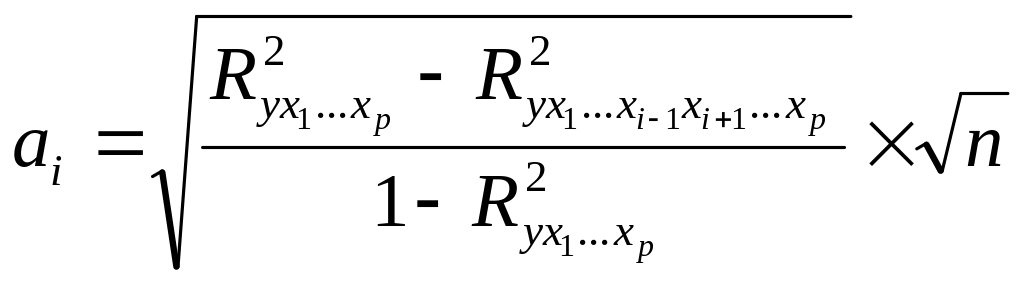15. Мультиколинеарность – это:

а) ненормальное распределение переменных;

б) взаимная коррелированность объясняющих переменных;

в) непостоянная для каждого значения фактора дисперсия;

г) взаимная некоррелированность объясняющих переменных.

16. Применение метода главных компонент позволяет:

а) предотвратить эффект мультиколинеарности;

б) ввести в модель новые объясняющие факторы, не зависящие от имеющихся;

в) избежать гетероскедастичности дисперсии остатков;

г) избежать автокорреляции остатков.

17. Введение новых переменных в модель множественной регрессии ограничивается:

а) остановкой роста скорректированного коэффициента детерминации;

б) отрицательным знаком параметра при новой переменной;

в) положительным знаком параметра при новой переменной;

г) отсутствием корреляции между объясняющими факторами.