Глава 2. Специальная часть

2.1 ВВВЕДЕНИЕ

2.1 Физические основы ЯМР

2.2 Методы измерений

2.2.1 Общие слова про керн и ГИС

2.2.2 Техническое описание аппаратурно-методического комплекса «Протон-20м»

2.3 Определение петрофизических характеристик горных пород стандартными методами

2.4 Определение петрофизических характеристик горных пород методом ЯМР

Годом открытия ЯМР считается 1945-й, когда американцы Феликс Блох из Стэнфорда и независимо от него Эдвард Парселл и Роберт Паунд из Гарварда впервые наблюдали сигнал ЯМР на протонах. К тому времени уже было много известно о природе ядерного магнетизма, сам эффект ЯМР был теоретически предсказан, и было сделано несколько попыток его экспериментального наблюдения. Важно отметить, что годом раньше в Советском Союзе, в Казани, Евгением Завойским было открыто явление электронного парамагнитного резонанса. Сейчас уже хорошо известно, что Завойский также наблюдал и сигнал ЯМР, это было перед войной, в 1941 году. Однако в его распоряжении был магнит низкого качества с плохой однородностью поля, результаты были плохо воспроизводимыми и потому так и остались неопубликованными. Справедливости ради надо заметить, что Завойский был не единственным, кто наблюдал ЯМР до его «официального» открытия. В частности, американский физик Исидор Раби (лауреат Нобелевской премии 1944 года за исследование магнитных свойств ядер в атомных и молекулярных пучках) в конце 30-х годов также наблюдал ЯМР, но счел это аппаратурным артефактом.

После создания спектрометров ядерного магнитного резонанса, Парселл разрабатывал методики измерения магнитных моментов ядер и частиц, исследовал молекулярные структуры, поведение ядер при низких температурах, измерял атомные константы. В 1948 г. совместно с Н. Бломбергеном и Р. Паундом ввел представление о спиновой температуре более высокой, чем температура решетки, а в 1951 г. с Паундом – о положительной и отрицательной спиновой температуре. В 1950 г. с Р. Паундом впервые наблюдал индуцированное излучение, осуществив инверсию населенностей ядерных систем путем быстрого изменения направления магнитного поля.

Исследования керна ямр-релаксометром Введение

Ядерный магнитный резонанс относится к методам квантовой радиофизики. В его основе лежит наблюдение эффектов, вызванных взаимодействием ядер, обладающих магнитным моментом, с окружающими микрочастицами при воздействии на всю систему постоянного и переменного магнитных полей. Методы ЯМР широко применяются в различных областях химии, биологии, геофизики и медицины.

По напряженности постоянного магнитного поля методы ЯМР классифицирут на ЯМР в Земном, слабом и сильном полях по величине напряженности, выраженной в Эрстедах (Э) или Гауссах (Гс):

• Земное (0,5 Э)

• Слабое (до 500 Э)

• Сильное (более 500 Э)

Метод ЯМР применяется как для каротажа, так и для лабораторных исследований керна. В основе метода ЯМР лежат три эффекта:

1. Ядерная намагниченнось

2. Ядерная прецессия

3. Ядерная релаксация.

Физические основы метода ямр

Физические процессы, происходящие при ЯМР, для наглядности и решения практических задач рассматриваются одновременно в рамках классической и квантовой механики.

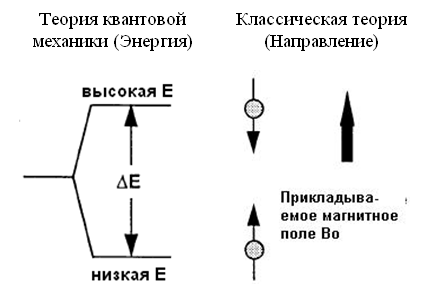Схематичная иллюстрация энергетического состояния протона.

Явление ЯМР наблюдалось на различных ядрах, имеющих нечетное количество протонов или нейтронов, например ядрах водорода ('Н), углерода (13С) или натрия (23Na).

Ядра атомов водорода обладают собственным механическим и магнитным μ моментами:

,

где h – постоянная Планка (h = 6,626∙10-34 Дж∙с),

I – спин (квантовое число, верчение) принимает только целые, полуцелые или нулевое значения. В частности, спин протона (ядра водорода) I = ½;

γ – гиромагнитное отношение, определяющее магнитные свойства ядра.

Магнитный и механический моменты ядра совпадают по направлению. Благодаря чему, в классическом представлении ядро можно уподобить волчку, у которого вдоль оси расположен магнит.

Будучи выведенными из равновесия, они прецессируют в статическом магнитном поле (слева) точно так же, как и макушка детского волчка в гравитационном поле Земли (справа).

При помещении ядер в постоянное магнитное поле с напряженностью Н их магнитные моменты μ стремятся ориентироваться в направлении вектора данного поля, что ведет к возникновению ядерной намагниченности М – сумме магнитных моментов единицы объема вещества:

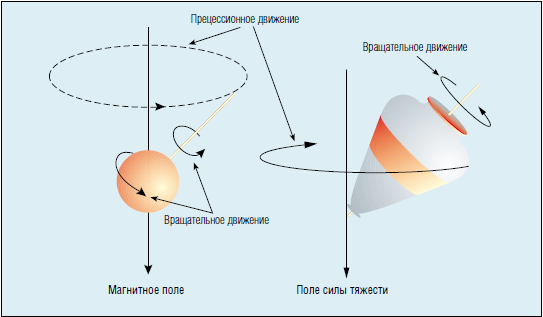
Рис. Прецессирующие протоны. Ядра водорода — протоны — ведут себя подобно вращающимся стержневым магнитам.

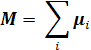
Во внешнем магнитном поле вектор ядерной намагниченности определяется следующим соотношением:

,

где æ – ядерная магнитная восприимчивость (≈10-10)

При снятии внешнего магнитного поля происходит разрушение приобретенной ядерной намагниченности из-за беспорядочного теплового движения атомов и молекул вещества. Так как это происходит в магнитном поле Земли, ядра ориентируются вдоль этого поля, прецессируя (совершая затухающее вращение) вокруг него подобно волчку в поле силы тяжести с так называемой Ларморовой частотой

.

Основной эффект, наблюдаемый методом ЯМР, состоит в излучении энергии на частоте ω.

Вектор ядерной намагниченности М имеет две составляющие - продольную = , совпадающую по направлению с внешним полем Н0, и поперечную = , перпендикулярную Н0.В стационарном состоянии = , = 0.

Если мы нарушим это состояние, например, наложением дополнительного постоянного магнитного поля Нд, не совпадающего по направлению с Н0, то вектор М примет направление суммарного поля Н = Н0 + Нд и возрастет по величине пропорционально Н. Если быстро отключить поле Нд, то начнется процесс возвращения вектора ядерной намагниченности М к своему первоначальному стационарному положению, то есть релаксация. Этот процесс растянут во времени. Скорость установления продольной компоненты (t) характеризуется постоянной во времени Т1, так называемой спин-решеточной или продольной релаксцией. А скорость установления поперечной компоненты (t) – временем спин-спиновой или поперечной релаксацией.

Экспоненциальное приближение к равновесному значению М0 описывается уравнением:

где t - время, в течение которого на протоны воздействует магнитное поле; - величина намагниченности на время t, когда направление поля H0 принимает положение, совпадающее с осью z; - окончательная и максимальная величина намагниченности данного поля.

Постоянная T1 означает период, в течение которого намагниченность достигает 63 % своего окончательного значения, а трехкратное Т1, означает время, за которое достигается 95 % поляризации (Рис. 2.10). Флюиды имеют различные времена поляризации T1, что находит широкое применение в промысловой геофизике.

Рис. 2.10. График изменения продольной релаксации во времени. Процесс намагничивания.

Таблица 2.4.

Флюид	Т1
Газ и Нефть	Медленное
Вода связанная	Быстрое
Вода свободная	Среднее

Времена поляризации Т1 для разных флюидов.

Выше было отмечено, что скорость затухания поперечной составляющей вектора ядерной намагниченности определяется спин-спиновым взаимодействием. Однако на поведение этой составляющей существенно влияет и неоднородность внешнего магнитного поля, которая приводит к тому, что частоты прецессии в разных элементарных объемах исследуемого образца отличаются на величину γΔНо, где ΔНо – разность напряженности поля в соседних точках образца. Поэтому реальная скорость затухания (t) определяется постоянной времени Т*2, которая меньше Т2:

Графически разницу между Т2* и Т2 хорошо видно в цикле CPMG для измерений ЯМР, который будет описан ниже (Рис.2.13.). Для наглядности можно совместить во времени графики для продольной и поперечной намагниченности (Рис. 2.11).

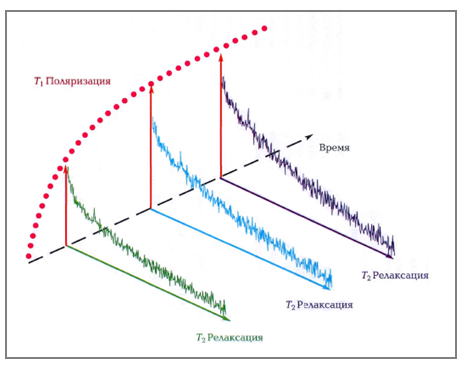
Рис.. Времена релаксации Т1 и Т2 (или поляризации и релаксации).

Т1 описывает скорость нарастания продольной намагниченности , а Т2 – скорость спада поперечной намагниченности .

Одновременное воздействие на систему спинов постоянного Н и переменного Н1 магнитного полей создает дополнительные эффекты. При кратковременном действии переменного магнитного поля вектор ядерной намагниченности повернется вокруг направления этого поля на угол φ:

φ = ω1t = γН1t,

пропорциональный напряженности переменного (осциллирующего) поля Н1 и времени его действия t. Это дает нам возможность получать восстановления времен релаксации, поворачивая магнитное поле одним или серией импульсов (т.е. единичным или серийным кратковременным включением переменного поля Н1). Термины угол-импульс, такие как импульс π (или стовосьмидесятиградусный импульс) и импульс π/2 (или девяностоградусный импульс), относятся к углу, на который осуществляется изменение направления намагниченности с помощью Н1.

Если под действием РЧ импульса намагниченность отклонится от оси z (т.е. от равновесного положения), то после выключения РЧ импульса намагниченность, в результате появления у нее поперечных компонент, начнет прецессировать вокруг направления поля Н0. Если мы поместим образец в приемную катушку, то изменяющееся во времени магнитное поле создаст малое индукционное напряжение, которое может быть зарегистрировано с помощью соответствующих методов. Амплитуда этого сигнала пропорциональна резонансной частоте ω и намагниченности M0; затухание сигнала во времени называют спадом свободной индукции (ССИ) или спадом свободой прецессии (ССП).

Спин- решеточная релаксация.

   

Ядерные спины всегда взаимодействуют со своим окружением (решеткой), но вследствие того, что это взаимодействие мало, допустимо различать спиновую температуру и температуру решетки. Однако, благодаря имеющемуся слабому взаимодействию между двумя системами, устанавливается тепловое равновесие. Поэтому необходимо рассмотреть скорость установления равновесия. Этот процесс играет существенную роль для установления природы ЯМР.

   Рассмотрим систему ядер, помещенную в постоянное магнитное поле  ₀ (поле  ₁ отсутствует). Для термического перехода, помимо взаимодействия системы спинов ядер с решеткой, требуется существование определенного энергетического состояния этой системы (решетки), при котором возможен переход. Это можно проиллюстрировать, предположив, что резервуар (решетка) имеет только два уровня энергии, расстояние между которыми точно такое же, как и у ядерной системы.

   Если ядро и резервуар вначале находятся в противоположных состояниях (рис. 4а), то одновременный переход, указанный стрелками, удовлетворяет закону сохранения энергии. Следовательно, ядро может отдавать энергию решетке. С другой стороны, если обе системы находятся в верхнем состоянии (рис. 4б), то одновременный переходневозможен, т.к. при этом не сохраняется энергия. Вероятности переходов с поглощением и испусканием одинаковы. При наличии спин- решеточного взаимодействия это равенство нарушается, т.к. в этом случае скорость ядерного перехода зависит от вероятности того, что резервуар находится в состоянии, при котором возможен переход.

 

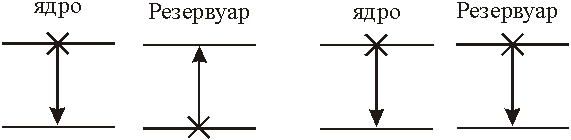
Рис.4. Переходы: а - разрешенный; б - запрещенный.

Возвращаясь к нашей системе, получим:

                     (n – n_равн.)=(n – n_равн.)₀exp(- t/T₁),                                                (2.18)

n – разность заселенности двух уровней или избыток заселенности.

   Т.о., разность между избыточным числом ядер в произвольный момент времени и его значение в состоянии теплового равновесия (т.е. к моменту, когда t=Т₁) уменьшится в е раз. Это времяхарактеризует скорость, с которой система ядерных спинов приходит в тепловое равновесие с другими степенями свободы данного образца (решетки). Величину Т₁ обычно называют временем спин- решеточной релаксации. В течение этого времени устанавливается разность заселенности уровней, отвечающая данному значению Н₀ и температуры. Результатом этой разности является появление результирующего макроскопического магнитного момента образца. Поэтому можно сказать, что Т₁ представляет собой время, необходимое для намагничивания образца.

   Процесс спин- решеточной релаксации приводит к уширению резонансной линии, т.к. переходы, индуцируемые другими степенями свободы молекулы, делают конечным время жизни ядра в данном состоянии. Порядок величины уширения, вызванного этим процессом, равна:

                      Dn»p¤2Dt,                                                                                     (2.19)

где Dn [Гц].

   В выражении (2.19) Dt – характеристическое время того процесса, который приводит неопределенностив значении резонансной частоты, т.е. обуславливает уширение сигнала. Т.о., ширина линии в единицах частоты, обусловленная спин- решеточной релаксацией, приблизительно равна 1/Т₁.

   Время спин- решеточной релаксации существенно зависит от окружающей среды и типа ядра. Передача магнитной энергии от протонов и других ядер со спином 1/2 к другим степеням свободы может происходить только одним путем – посредством флуктуаций локальных магнитных полей. Ядра с более высокими значениями спина имеют электрические квадрупольные моменты, которые могут взаимодействовать с флуктуирующими электрическими полями. Поэтому значения Т₁ для таких ядер меньше. Для жидкостей значения времен спин- решеточной релаксации лежат в пределах 10^-2 – 10² с. в твердых телах Т₁ меняется от 10^-4 – 10⁴ с.

Спин- спиновая релаксация.  

   Кроме взаимодействия с решеткой, ядра могут также взаимодействовать между собой. Этот процесс характеризуется временем спин- спинового взаимодействия, которое обозначается обычно как Т₂. На каждый магнитный момент ядра действуют не только постоянное магнитное поле Н₀, но и слабое локальное магнитное поле  _лок, создаваемое магнитными ядрами. Магнитный диполь на расстоянии r создает поле m/r³.

   С ростом r напряженность поля  _лок быстро падает, так что существенное влияние могут оказывать только ближайшие соседние ядра. По этой причине разные ядра оказываются в разных постоянных магнитных полях. Результатом чего должен быть разброс (неопределенность) значений энергетических уровней совокупности резонирующих ядер, т.е. неопределенность частоты резонансных сигналов, и как следствие этого – уширение линий. Изменение ориентации и диффузия молекул в жидкостях, газах и некоторых твердых телах происходят обычно настолько быстро, что локальное магнитное полеусредняется до очень малой величины (10⁴ – 10⁵ раз) по сравнению с  _лок для жесткой решетки, т.е. при фиксированном относительно друг друга расположении ядер. В соответствии с таким усреднением наблюдаются узкие резонансные линии. По величине разброса локального поля  _лок с помощью уравнения резонанса можно найти разброс частоты ларморовой прецессии:

                                                       Dn=m _лок/Iħ.                                              (2.20)

   Если в какой- либо момент времени ядерные диполи прецессируют в фазе, то время, необходимое, чтобы фазы прецессии разошлись, равно (Δν)^-1. это время можно рассматривать как часть времени Т₂.

   Существует еще один аспект взаимодействия соседних ядер (магнитных диполей), который также следует учитывать при изучении причин уширения линий. Ядерные спины даже в твердых телах прецессируютвокруг направления внешнего магнитного поля  ₀. Поэтому создаваемые ими локальные поля можноразложить на статическую компоненту  _ст (направленную вдоль  ₀) и осциллирующую  _осц. Эта компонента создает магнитное поле, которое может индуцировать переходы соседнего ядра, если это ядро прецессирует с той же частотой. В результате ядро j, создающее магнитное поле, осциллирующее с ларморовой частотой, может вызвать переход у ядра i. Энергия для такого процесса берется от ядра j, и происходит одновременная переориентация (переброс) обоих ядер, т.е. обмен энергией при сохранении общей энергии ядер (рис.5.).

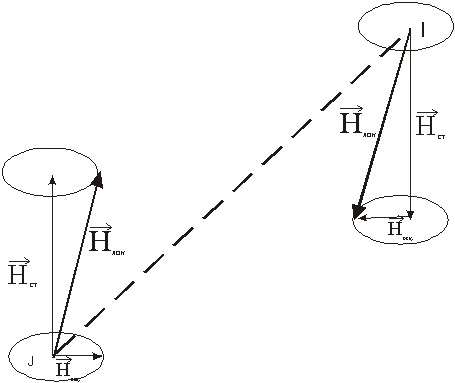
Рис.5. Локальные поля, создаваемые ядерным магнитным диполем.

   Однако время жизни каждого из них на данном энергетическом уровне уменьшается. Поскольку относительные фазы ядер изменяются за время (Δν)^-1, то для спинового обмена требуется интервал времени такого же порядка. Этот процесс вызывает дальнейшее уменьшение времени Т₂, т.е. уширениерезонансной линии (наблюдаемое при фиксированной частоте) на величину порядка  _лок. Оба эти фактора учитываются в величине Т₂, которая определяется как время жизни спинов в определенном состоянии и которая представляет собой величину, обратную ширине спектральной линии:

                                                     Т₂=1/(πΔν).                                                   (2.21)

   Дипольное уширение и спин- спиновый обмен – это не только лишь два подхода к интерпретации одного итого же явления. В образце, содержащем ядра А и В, не может быть взаимного спин- спинового обмена между данными ядрами, т.к. частоты прецессии сильно различаются. Однако дипольное взаимодействие между ядрами А и В будет наблюдаться, а следовательно, и уширение сигнала.

   Следует отметить, что кроме спин- решеточной и спин- спиновой релаксации имеются иные причиныуширения линий ЯМР. К этому приводит неоднородность постоянного магнитного поля  , т.к. в действительности получается наложение линий поглощения от молекул, находящихся в различных частях образца. На форму линии, а значит и на ее ширину, могут влиять насыщение, нестационарные (переходные) процессы, а также технические характеристики аппаратуры.

Магнитный момент - основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток. Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина. Магнитный момент измеряется в А⋅м2 или Дж/Тл (СИ), либо эрг/Гс (СГС), 1 эрг/Гс = 10-3 Дж/Тл.

В случае плоского контура с электрическим током магнитный момент вычисляется как

,

где I — сила тока в контуре, S — площадь контура, — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.

Для произвольного замкнутого контура магнитный момент находится из:

,

где — радиус-вектор, проведенный из начала координат до элемента длины контура

В общем случае произвольного распределения токов в среде:

,

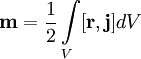где — плотность тока в элементе объёма dV.

Мо равновесная намагниченность - определяет порядок величины резонансного поглощения: Мо = Хо Н0, где xо - статич. ядерная восприимчивость.

Намагниченность - векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно М или J. Определяется как магнитный момент единицы объёма вещества:

Здесь, M — намагниченность; m вектор определяющий магнитный момент; V — объём.

Свойство веществ, горных пород, минералов, определяемое магнитным моментом единицы объема и в общем случае характеризующее их способность к созданию магнитных полей.

Ядерная намагниченности – (М) вектор, который описывает конус, угол раствора которого Θ определяется расстройкой частоты радиоимпульса относительно частоты прецессии: cos Θ = ∆ ω/ ωэф . При малых расстройках – H»Ho—ω/γ, ωэф ≈ ω1 ─ конус вырождается в плоскость zoy. Если при этом длительность импульса

τ=π/2 ω1,

то в момент τ вектор →М будет находиться в плоскости χoy (90°-ный импульс).

Ядерная прецессия - когда атом вещества находится в магнитном поле, магнитный момент его ядра вынуждает ядро прецессировать (эффект, аналогичный действию силы тяжести на вращающийся волчок, заставляющей качаться его ось). Частота, или скорость, прецессии ядра зависит от величины магнитного поля и от магнитного момента ядра. Таким образом, если известна сила поля и удается определить частоту прецессии, то можно вычислить магнитный момент. Для того чтобы определить частоту прецессии, образец исследуемого материала помещается в магнитное поле мощного электромагнита, вынуждая ядра образца прецессировать с постоянной скоростью.

В данной дипломной работе применялись два метода:

1. Для изучения продольной релаксации Т₁ использовались два девяностоградусных импульса, то есть метод 90 – τ – 90, где τ – это время между первым и вторым импульсом.

2. Для изучения поперечной релаксации Т₂ использовался цикл КПМГ.

Цикл Карра-Пурселла-Мейбума-Гилла (КПМГ, CPMG).

Последовательный ряд импульсов, первый из которых 90-градусный, за которым следует серия 180-градусных импульсов, называется циклом Карра-Пурселла-Мейбума-Гилла. Этот метод основан на создании серии эхо-сигналов. Процедура измерения начинается с ориентирования протонов, после чего следуют отклонение спинов, прецессия, расфазировка и рефокусировка. Затухающий сигнал называется спадом свободной индукции (ССИ), а время затухания — Т₂*, где звездочка означает, что данное затухание не является свойством породы. У каротажных приборов величина Т₂* сравнима с длительностью отклоняющего импульса, т.е. составляет несколько десятков микросекунд.

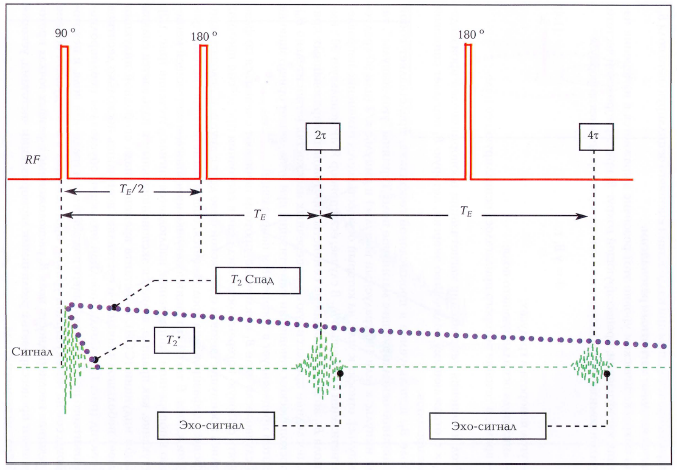
Рис.. Цикл CPMG для измерения Т₂.

Константа времени спада поперечной релаксации называется временем поперечной релаксации и обозначается как Т₂. Амплитуда серии эхо спина при времени t, являющаяся амплитудой поперечной намагниченности , вычисляется по формуле

,

где - величина поперечной намагниченности при t = 0 (время, при котором заканчивается 90⁰ импульс).

Спад эхо-сигналов (рис..), который зависит от количества и распределения водорода во флюидах, измеряется записью снижения амплитуды релаксации во времени.

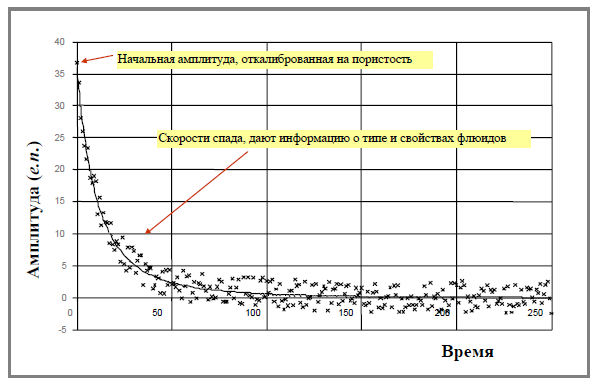
Рисунок. Спад эхо-сигналов.

Продольная поперечная релаксации.

Продольная (Т₁) и поперечная (Т2) релаксации вызываются магнитными взаимодействиями между наблюдаемыми протонами и другими ядрами, С ато­марной точки зрения релаксация Т₁ происходит тогда, когда прецессирующая система протонов передает энергию своему окружению, и называется спин-ре­шеточной релаксацией. Релаксация Т₂, обусловлена спин-спиновым воздействием ядер и всегда происходит быстрее, чем продольная; следовательно, время Т₂ всегда меньше или равно Т₁.

Существует три типа релаксации ЯМР в реальной породе, которые обладают различными временами действия:

• релаксация на поверхности зерен (T_s);

• релаксация в результате диффузии молекул (T_D);

• релаксация в поровых флюидах (объемная) (Т_в).

Все три процесса действуют одновременно, и времена Т₁ и Т₂ поровых флюидов выражаются как:

,

Относительный вклад каждого из механизмов зависит от типа флюида в порах (вода, нефть или газ), размера пор, силы поверхностной релаксации и смачиваемости поверхности породы. В общем случае для гидрофильного кол­лектора:

Поверхностная релаксация возникает за счет эффектов взаимодействия протонов с поверхностью зерен и контролируется распределением пористости по размерам пор, формой пор и релаксационной активностью поверхности.

Согласно теоретическим разработкам принципа ограниченности быстрой диффузии основную составляющую Ts можно определить по формуле:

,

где - поверхностная релаксивность;

- удельная поверхность порового пространства.

Для простых форм удельная поверхность — это функция размера пор. На­пример, для модели с набором идеальных сфер она составляет 3/r, где r — радиус сферы.

Поверхностная релаксивность зависит от минералогии породы; так, на карбонатной поверхности она слабее, чем на кварцевой.

Диффузионная релаксация проявляется в неоднородном магнитном поле, где молекулярное движение вызывает расфазировку протонов. Она возникает, в частности, при использовании средств измерений, формирующих неоднородное магнитное поле, например, как при ЯМТК (Томографический ЯМР-каротаж). Диффузия не оказывает воздействия на скорость спада сигнала Т₁.

Объемная релаксация определяется собственно свойствами флюида, насыщающего поровое пространство. Эффект объемной релаксации слабее поверхностной и становится заметным, когда взаимодействие протонов с поверхностью ограничено, например, при лабораторных ЯМР-исследованиях пластовых флюидов, в кавернозных карбонатах, для углеводородов в гидрофильных коллекторах (протоны УВ не контактируют с поверхностью пор).