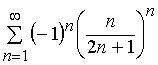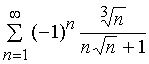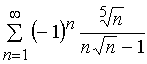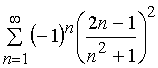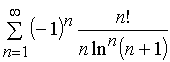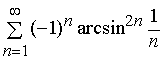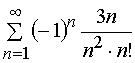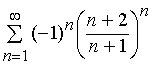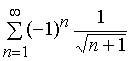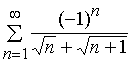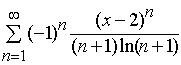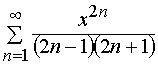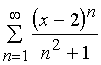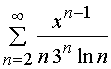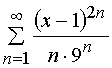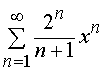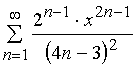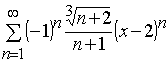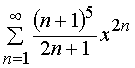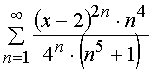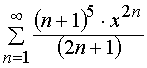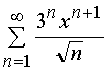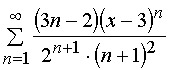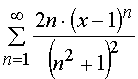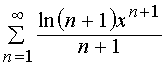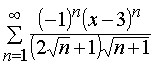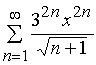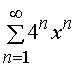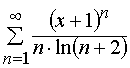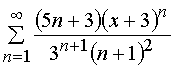3. Задания для самостоятельной работы на 2 семестр
3.1. Типовой расчет №3
Функции нескольких переменных.
Кратные интегралы. Дифференциальные уравнения.
Задача 1 – 10. Найти наибольшее и наименьшее значения функции z = f (x; y) в ограниченной замкнутой области D. Область D изобразить на чертеже.
1. Z = x2 – y2 + 3xy + 7 ; D : -2 x 2, -2 y 2 .
2. Z = x2 + 2y2 – 1 ; D : x -2, y -2, x + y 4 .
3. Z = 3 – x2 – xy – y2 ; D : x 1, y -1, x +1 y .
4. Z = x2 + y2 + x – y ; D : x 1, y -1, x + y 2 .
5. Z = x2 +2xy +2y2 ; D : -1 x 1, -1 y 3 .
6. Z = 3x2 – 3xy +y2 + 1 ; D : x -1, y -1, x + y 1 .
7. Z = 5 + 2xy – x2 ; D : -1 y 4 – x2 .
8. Z = x2 – 2xy – y2 + x ; D : x 0, y 1, x + y + 2 0 .
9. Z = x2 – xy – 2 ; D : 4x2 – 4 y 1 .
10. Z = x2 + xy + 3y2 ; D : -1 x 1, -1 y 1 .
Задача 11 – 20.
Даны: функция трех переменных u = f (x, y,
z), точка
M0 (x0;
y0; z0) и вектор
(а1,
а2,, а3) .
Найти:
1) grad u в точке М0;
2) производную в точке М0 по направлению вектора ;
3) наибольшую крутизну поверхности u = f (x, y, z) в точке М0.
11.
M0 (1;
-2; 1) ;
(-1;
2; 2) .
12. u = ln|3x2 – 2y + z| ; M0 (1; 1; 0) ; (0; 4; 3) .
13.
M0 (1;
1; 2) ;
(-3;
0; 4) .
14.
M0 (1;
2; 2) ;
(3;
0; -4) .
15.
M0 (2;
2; 1) ;
(1;
-2; 2) .
16. u = ln|10 – x2 – y2 – z2| ; M0 (2; 2; 1) ; (-4; 0; 3) .
17.
M0 (3;
4; 0) ;
(2;
-1; 2) .
18. u = x2y2 + x2z2 + y2z2 ; M0 (-1; 2; 1) ; (0; 6; 8) .
19.
M0 (3;
4; 0) ;
(2;
2; -1) .
20. u = ln|12 – x2 – y2 + z| ; M0 (1; 1; -5) ; (3; 0; -4) .
Задача 21 – 30. Вычислить двойной интеграл по области D . Область интегрирования D изобразить на чертеже.
21.
D : y = x2
, y = 2 – x2
.
22.
D : x = 1 , y = x2
, y = 0 .
23.
D : y = x , y = x3
, x
0 .
24.
D : y = x2
, y =
.
25.
D : x = 1 , y =
,
y = -x2
.
26.
D : x = 1 , y = x2
, y = 0 .
27.
D : y = x2
, y =
.
28.
D : x = 1 , y =
y = -x3
.
29.
D : y = x , y =
.
30.
D : x = 1 , y = x2 , y = -
.
Задача 31 – 40. Найти решения дифференциальных уравнений первого порядка, удовлетворяющие указанным начальным условиям.
31 .
,
.
32.
,
.
33.
,
.
34.
,
35.
,
36.
,
.
37.
,
38.
,
39.
,
40.
,
Задача 41 – 50. Решить дифференциальные уравнения второго порядка: а) найти общее решение; б) найти решение, удовлетворяющее указанным начальным условиям.
51. а)
.
б)
,
,
52. а)
.
б)
,
,
53. а)
б)
,
,
54. а)
б)
,
,
55. а)
б)
,
,
56. а)
б)
,
,
57. а)
б)
,
,
58. а)
б)
,
,
59. а)
б)
,
,
60. а)
б)
,
,
Задача 61 – 70. Найти решение задачи Коши:
3.2. Типовой расчет №4
Ряды. Криволинейные интегралы.
Задача 1 – 10. Выяснить, какие из данных рядов сходятся и какие расходятся. Для знакочередующихся рядов выяснить также (в случае сходимости) абсолютную или условную сходимость.
1. а)
,
б)
.
2. . а)
,
б)
.
3. а)
,
б)
.
4. а)
,
б)
.
5. а)
,
б)
.
6. а)
,
б)
.
7. а)
,
б)
.
8. а)
,
б)
.
9. а)
,
б)
.
10. а)
,
б)
.
Задача 11 – 20. Исследовать на сходимость знакопеременные ряды:
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|
|
|
|
|
Задача 21 – 30. Найти интервал сходимости степенного ряда:
21. а) |
б)
|
22. а)
|
б)
|
23.
а) |
б)
|
24. а)
|
б)
|
25 а) |
б)
|
26. а) |
б)
|
27. а) |
б)
|
28. а) |
б)
|
29. а) |
б)
|
30. а) |
б)
|
Задача 31 – 40. Определить область сходимости данных рядов.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
Задача 41 – 50.
Разложить функцию
в ряд Фурье в указанном интервале.
Выписать полученный ряд и три первых
члена разложения отдельно.
41.
в
интервале
.
42.
в
интервале
.
43.
в
интервале
.
44.
в
интервале
.
45.
в
интервале
.
46.
в
интервале
.
47.
в
интервале
.
48.
в
интервале
.
49.
в
интервале
.
50.
в
интервале
.
Задача 51 - 60. Вычислить криволинейный интеграл. Сделать чертеж дуги кривой L.
51.
,
где L – отрезок прямой от точки (1;
0) до точки (0; -1).
52.
,
где L – отрезок прямой от точки (2;
0) до точки
.
53.
,
где L – дуга кривой y = ln x от точки
(1; 0) до точки (е; 1).
54.
,
где L – дуга кривой y = x2 от
точки (1; 1) до точки (2; 4).
55.
,
где L – верхняя половина окружности
x = sin2t, y = cos2t. Интегрировать в направлении
против часовой стрелки.
56.
,
где L – дуга кривой y = x2 от
точки (0; 0) до точки (1; 1).
57.
,
где L – первая четверть окружности
x = 2cost, y = 2sint. Интегрировать в
направлении против часовой стрелки.
58.
,
где L – отрезок прямой от точки (1;
2) до точки (2; 4).
59.
,
где L – дуга кривой y = x2 от
точки (1; 1) до точки (2; 4).
60.
,
где L – верхняя половина эллипса
x = 4sint, y = 3cost. Интегрировать
в направлении против часовой стрелки.