2.6. Розширений мінімаксний китерій

Розглянемо на завершення ще один метод, що допускає інтепретацію в якості розширеного мінімаксного критерію. У ньому використовуються найпростіші поняття теорії імовірності, а також, у деякій мірі, теорії ігор. Читач може, проте, при першому читанні пропустити цей розділ, оскільки в технічних додатках цей критерій досі застосовується мало.

Основним тут є припущення про те, що кожному з п можливих зовнішніх станів F_j приписана ймовірність його появи q_j :

Сформуємо з п ймовірностей q_j вектор q=(q₁,…, q_n} і позначимо через W⁽ⁿ⁾ множину всіх n-мірних ймовірнісних векторів. Вибір якогось варіанту рішення Е_і призводить при достатньо довгому застосуванні E_i до середнього результату Якщо ж тепер випадковим чином з розподілом ймовірностей змішати т варіантів рішень E_i, то в результаті одержимо середнє значення

У реальній ситуації вектор q= (q₁,…,q_n), що відноситься до стану F_j, буває, як правило, невідомим. Орієнтуючись щодо значення е(р, q) на найменш вигідний розподіл q станів F_j і добиваючись, з іншого боку, максимального збільшення е(р, q) за рахунок вибору найбільше вдалого розподілу р варіантів рішення E_i, одержують у результаті значення, що відповідає розширеному ММ-критерію.

Позначимо тепер через Е(р) узагальнений варіант рішення, що визначається за допомогою вибору ймовірнісного вектора а через – множину всіх таких варіантів.

Тоді розширений ММ-критерій формулюється в такий спосіб:

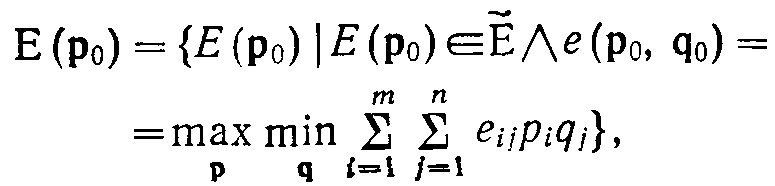(3.18 )

де р - ймовірнісний вектор для E_i, a q - ймовірнісний вектор для F_j.

Таким чином, розширений ММ-критерий задається метою знайти найвигідніший розподіл ймовірностей на множині варіантів E_i, коли в ситуації , що багаторазово воспроизводится , нічого не відомо про можливості станів F_j. Тому передбачається, що F_j розподілені найменш вигідним способом.

2.7. Застосування класичних критеріїв

З вимог, запропонованих розглянутими критеріями до аналізованої ситуації, стає ясно, що внаслідок їх жорстких вихідних позицій вони застосовні тільки для ідеалізованих практичних рішень. У випадках, коли потрібна занадто сильна ідеалізація, можна одночасно застосовувати по черзі різноманітні критерії. Після цього серед декількох варіантів, відібраних таким чином в якості оптимальних, доводиться усе-таки примусово виділяти деяке остаточне рішення . Такий підхід дозволяє, по-перше, краще проникнути в усі внутрішні зв'язки проблеми прийняття рішень і, по-друге, послабляє вплив суб'єктивного чинника.

Вибір рішення за класичними критеріями проілюструємо таким прикладом.

Нехай деяку машину (технологічну установку, конвеєр, верстат і т.п.) потрібно піддати перевірці з припиненням, звичайно ж, її експлуатації. Через це припиняється випуск продукції. Якщо ж експлуатації машини перешкоджає не виявлена своєчасно несправність, то це призведе не тільки до припинення роботи, але і додатково до поломки.

Варіанти рішення такі:

E₁ - повна перевірка;

E₂ - мінімальна перевірка;

Е₃ - відмова від перевірки.

Машина може знаходитися в таких станах:

F₁ - несправностей немає;

F₂ - є незначна несправність;

F_j - є серйозна несправність.

Результати включають витрати на перевірки й усунення несправності, а також витрати, пов'язані з втратами в продукції і з поломкою.

Таблиця 2.2.

Варіанти рішення про перевірки машини і їхньої оцінки (у 10³) відповідно до ММ- і BL-критеріїв для q_j= 0,33

	F 1	F2	F3	MM - критерій		BL - критерій
				eir=min eij	max eir	eir=eijqj	Max eir
E1 E2 E3	-20,0 -14,0 0	-22,0 -23,0 -24,0	-25,0 -31,0 -40,0	-25,0 -31,0 -40,0	-25,0	-22,33 -22,67 -21,33	-21,33

Вони приведені в табл. 2.2. Відповідно до ММ-критерію (3.3), варто проводити повну перевірку (E₀={E₁}). BL - критерій у припущенні, що всі стани машини рівноймовірні (q_j=0,33), рекомендує відмовитися від перевірки (E₀={E₁}). Табл. 3.3 ілюструє застосування S-критерію. Їм у якості оптимальної рекомендується мінімальна перевірка.

Наш приклад свідомо обраний так, що кожний критерій пропонує нове рішення. Невизначеність стану, у якому перевірка застає машину, перетворюється тепер у відсутність ясності, якому ж критерію слідувати. Таким чином, ми начебто б мало що виграли. Якнайбільше, можна було б

Таблиця 2.3.

Матриця залишків для прикладу «Рішення про перевірки машини»

і їхня оцінка (у 10³) відповідно до S-критерію

	F1	F2	F3	S - критерій
				eir=max aij	min eir
E1 E2 E3	+20,0 +14,0 0	0 +1,0 +2,0	0 +6,0 +15,0	+20,0 +14,0 +15,0	+14,0

перевірити після цього, чи приймають величини e_ir для якого-небудь критерію приблизно рівні значення, як, наприклад, е_2r= 14,0*10³ і e_3r= 15,0*10³ у табл. 2.3; рекомендації такого критерію виглядають менш переконливими. Оскільки різноманітні критерії пов'язані з різними аспектами ситуації, у якій приймається рішення, найкраще для порівняльної оцінки рекомендацій тих або інших критеріїв одержати додаткову інформацію про саму ситуацію. Якщо прийняте рішення відноситься до сотень машин з однаковими параметрами, то доцільно притримуватися BL-критерію. Якщо ж число реалізацій невелике, то більша вагу одержують більш обережні рекомендації S- або ММ-критеріїв.

У області технічних задач різноманітні критерії часто приводять до одного результату. Припустимо, що в аналізованому прикладі серйозна несправність (стан F₃) зустрічається вдвічі частіше, ніж будь-який інший стан (q₁=q₂; q₃=0,5), тоді BL-критерій, як і ММ-критерий, рекомендує повну перевірку (E₀={E₁}).

Бувають і такі ситуації, коли всі критерії дають однакові результати. Якщо для нашого приклада (табл. 2.2) за допомогою відповідних заходів удасться так знизити витрати на повну перевірку, що у відповідному рядку ми будемо мати e₁₁=-18,0*10³, e₁₂= -20,0*10³ і e₁₃= -22,0*10³, то всі три критерії рекомендуватимуть повну перевірку.

Будь-який варіант, що обирається в даному випадку всіма розглянутими критеріями, є слабко домінуючим. Сильне домінування має місце, коли для всіх результатів е_1j одного з аналізованих варіантів справедливо

е_1j  е_ij для j=1, ..., п і

е_1j<е_ij, хоча б для одного j.

Над зазначеним варіантом E₁ інші варіанти домінують. Його можна виключити з матриці рішень, тому що для всякого F, він дає гірший результат за інші.

Якщо якийсь варіант Е₁ домінує сильно, тобто виконуються умови

е_1j  e_ij для усіх j=1, ..., п та

е_1j >е_ij хоча б для одного j,

то навіть при відсутності інформації про можливі зовнішні стани F_j ніякої проблеми щодо прийнятого рішення немає. Для всякого F_j варіант Е₁ – найкращий.