3.2.3 Расчет по наклонному сечению

q₁=q=19,975 кН/м

Поскольку п. 5.26 /1/ допускает не устанавливать поперечную арматуру в многопустотных плитах, выполняю проверку прочности сечения плиты на действие поперечной силы при отсутствии поперечной арматуры согласно п. 3.32 /1/.

Рисунок 5 – Расчетная схема многопустотной плиты для расчетов по I группе предельных состояний.

Проверим условие 72 [3]

2,5 R_bt b h₀>

2.5 1.3 310 190=191.425 кН>56.93кН, т.е. условие выполняется

Проверим условие 93 [3], принимая упрощенно Q_b1=Q_bmin

С=2,5h₀=2.50.19=0.475м

Из п. 3.32 /1/ для лёгкого бетона при марке по плотности D1800

Нахожу усилие обжатия от растянутой продольной арматуры

По формуле (79) /1/:

Согласно п. 3.31 /1/ ,

Проверяю условие (93) /3/

Для обеспечения прочности поперечных сечений требуется поперечная арматура. Поперечная арматура устанавливается в рёбрах как показано на рисунке 4. Поперечную арматуру законструируем из арматуры класса Ат-VI d=3мм (А_sw=11*7,1=78,1мм², R_sw=650МПа, Е_s=1,9·10⁴МПа) с шагом s=100мм.

Согласно формуле (72) /1/ проверяю прочность по наклонной полосе ребра плиты между наклонными трещинами.

Для лёгких бетонов β=0,02

таким образом прочность бетона рёбер плиты обеспечена.

Прочность наклонных сечений по поперечной силе проверяю из условия (75) /1/. Так как для одного ребра имеем

, то принимаем в расчете все 11 рёбер. Тогда для всей плиты , тогда

Поскольку , то принимаю

Определяю M_b и q_sw.

Согласно п.3.32 /2/определяем длину проекции опасного наклонного сечения с, так как 0,56·q_sw=0,56·507,65=284,284 кН/м >q₁=19,975 кН/м значение с определяется по формуле:

Окончательно принимаю с=0,95м.

Длина проекции наклонной трещины равна

Так как принимаю с₀=0,29м, тогда

, т.е. прочность наклонного сечения по поперечной силе обеспечена.

Требования п. 3.32 /1/ также выполняются, поскольку

, кроме того удовлетворены требования п. 5.27 /1/ поскольку

3.3 Расчет по II группе предельных состояний

Согласно таблице 2 /1/, пустотная плита, эксплуатируемая в закрытом помещении и армированная напрягаемой арматурой класса Ат-V I диаметром 8мм, должна удовлетворять 3 категории требований по трещиностойкости, т. е. допускается непродолжительное раскрытие трещин шириной a_crc1=0,3мм и продолжительное – a_crc2=0,2мм. В соответствии с таблицей 19 /7/ прогиб плиты от действия постоянной и длительной нагрузок не должен превышать f_u=29,7мм.

3.3.1 Определение геометрических характеристик

Геометрические характеристики плиты рассчитаны вручную.

Определение геометрических характеристик приведенного сечения.

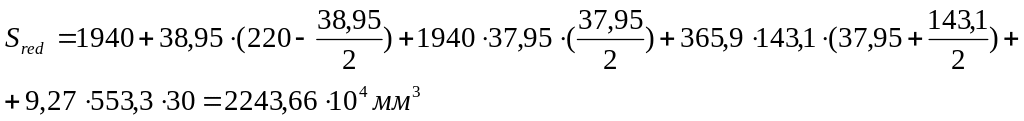
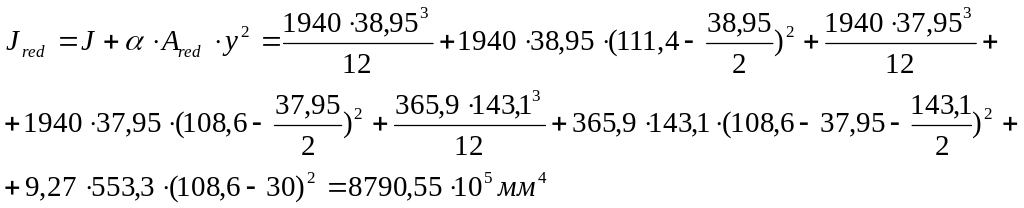
По таблице 38 [4] для двутаврового сечения при =1,5

3.3.2 Определение потерь предварительного напряжения

Определяю первые потери предварительного напряжения по позициям 1-6 таблицы 5 /1/:

Потери от релаксации напряжений в арматуре:

Потери от деформации анкеров в виде инвентарных зажимов

,

Таким образом усилие обжатия Р₁ с учетом потерь по позициям 1-5 таблицы 5 /1/ равно:

Точка приложения усилия Р₁ совпадает с центром тяжести сечения напрягаемой арматуры, поэтому e_op=y₀-a=10 8-30=78мм.

Для определения потерь от быстронатекающей ползучести бетона необходимо вычислить напряжения в бетоне в середине пролёта от действия силы Р₁ и изгибающего момента M_w от собственного веса плиты. Нагрузка от собственного веса плиты равна q_sw=2,39·2=4,78 кН/м (из таблицы 3), тогда момент от собственного веса плиты равен

Напряжение на уровне растянутой арматуры (y=e_op=78мм) будет равно:

Напряжение на уровне крайнего верхнего волокна (y=h-y₀=220-108=112мм):

Назначаю передаточную прочность удовлетворяющую требованиям п. 26 /1/.

Потери от быстронатекающей ползучести

потери на уровне растянутой арматуры

потери на уровне крайнего сжатого волокна

Первые потери: , тогда усилие обжатия с учетом первых потерь определяется:

Определяю максимальные сжимающие напряжения в бетоне от действия силы Р₁ без учёта собственного веса, принимая y=y₀=108мм

Поскольку , требования п.1.29 /1/ удовлетворены

Определяю вторые потери предварительного напряжения по позициям

7-11 таблице 5 /1/

Потери от усадки лёгкого бетона

Напряжения в бетона от действия силы Р₁ и изгибающего момента M_w:

,

Вторые потери равны:

Суммарные потери предварительного напряжения в арматуре:

, поэтому согласно п.1.25 /1/ потери не увеличиваем.

Усилие обжатия с учетом суммарных потерь будет равно: