8.4. Экономика
Предмет, функции и методы экономики.
Экономические законы и экономические категории.
Экономические блага и их классификация.
Экономические ресурсы и их виды.
Спрос. Факторы спроса. Закон спроса.
Предложение. Факторы предложения. Закон предложения.
Основные макроэкономические показатели.
Цикличность развития экономики. Фазы экономического цикла.
Денежно-кредитная политика. Кредит и его принципы.
Совокупный спрос и предложение. Кривые совокупного спроса и предложения.
8.5. Бухгалтерский учет 1. Задачи и общие принципы организации бухгалтерского учета.
Нормативные документы, регулирующие порядок учета кассовых операций
Понятие дебиторской и кредиторской задолженности
Формы и системы оплаты труда
Формирование стоимости объектов основных средств в зависимости от источников поступления
Учет заготовления и приобретения материальных ценностей
Затраты на производство, их состав и классификация по элементам
Учет доходов будущих периодов
Учет уставного капитала
Состав и содержание бухгалтерской отчетности.
9. Перечень практических заданий
Найти минимум затрат, используя СИМПЛЕКС МЕТОД Функция цели:
При ограничения:
Для решения использовать пакет Managlab.
Найти максимум прибыли, используя СИМПЛЕКС МЕТОД Функция цели:
При ограничения:
Для решения использовать пакет Managlab.
Найти максимум прибыли, используя СИМПЛЕКС МЕТОД Функция цели:
При ограничения:
Для решения использовать пакет Managlab.
Найти минимум затрат, используя СИМПЛЕКС МЕТОД Функция цели:
При ограничения:
Для решения использовать пакет Managlab.
Найти максимум прибыли, используя СИМПЛЕКС МЕТОД Функция цели:
При ограничения:
Для решения использовать пакет Managlab.
Решение задачи нелинейного программирования с помощью Excel. Найти максимальное значение целевой функции
При ограничения:
Найти максимальное значение выпускаемой продукции (целевой функции)
При ограничения:
Найти максимальное значение выпускаемой продукции (целевой функции)
При ограничения:
Найти максимальное значение выпускаемой продукции (целевой функции)
При ограничения:
Используя электронные таблицы EXCEL, определить местоположение транспорта от места поставки продукции к потребителям при обобщенном распределении Эрланга направлений движения (методом Монте-Карло)
При
Для получения требуемого результата использовать следующий алгоритм:
Задать для зоны обслуживания в 25 км (то есть 50-ти кварталов длиной 1кв = 0,5 км) распределение Эрланга направления выбора движения с математическим ожиданием «восток». Для этого использовать цифровой код направления движения: 1- север, 3 - юг, 2 - восток, 4 - запад. Полагать, что 1-й час объект перемещается в направлении 1, 2-й в направлении 2, 3-й в направлении 3, , 4-й в направлении 4.
Построить диаграмму распределения направлений.
Дана технологическая матрица межотраслевого баланса для трехотраслевой экономической системы и вектор конечной продукции этой системы. Определить вектор валового выпуска продукции. Определить, как необходимо изменить вектор валовой продукции, если конечный продукт первой отрасли необходимо увеличить втрое, а последней уменьшить вдвое.
0.1 0.4 |
0.2 |
250000 |
0.3 0.1 |
0.4 |
150000 |
0.1 0.3 |
0.1 |
200000 |
Имитационное моделирование местоположения транспорта при нормальном законе распределения направления движения.
Используя электронные таблицы EXCEL, определить удаленность транспортного средства от исходного места методом Монте-Карло .при Гауссовском распределении направлений движения.
Для получения требуемого результата использовать следующий алгоритм: • Задать для пройденного расстояния в 50 км (100 кварталов длиной 1кв = 0,5 км) нормально распределенные направления выбора движения с математическим ожиданием «юго-восток». Для этого использовать цифровой код направления движения: 1- север, 2 - юг, 3 - восток, 4 - запад и оценку распределения направлений движения
НОРМРАСП(А...; 2,5; 1,0; ЛОЖЬ). А... - ячейка с указанием каждого из направлений перемещения.
Построить диаграмму распределения направлений.
Отдельным столбцом для каждого из направлений отобразить факт его выбора единицей, факт невыбора - нулем. Для этого использовать логическую функцию.
Построить диаграмму индикаторов направлений.
Автосуммированием рассчитать число кварталов перемещения в каждом из направлений.
В отдельной ячейке отобразить удаленность от места побега, рассчитанную по формуле
.
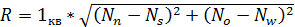Повторить вычислительный эксперимент М раз, задавая число направлений движения, обеспечивающее максимально близкое к требуемой значение вероятности каждого направления и зафиксировать полученные удаленности R в отдельном столбце.
По полученным М данным случайных R построить гистограмму распределения зоны удаления от места побега с дискретным шагом в 0,1 км. Рассчитать вероятность нахождения в каждой зоне и отобразить ее графиком.
Используя электронные таблицы EXCEL, определить удаленность транспорта с товаром от места погрузки методом Монте-Карло.
Для получения требуемого результата использовать следующий алгоритм:
Задать для пройденного расстояния в 25 км (то есть 50-ти кварталов длиной 1кв = 0,5 км) равномерно распределенные направления выбора движения. Для этого использовать генератор случайных чисел с равномерным законом распределения СЛУЧМЕЖДУ() и цифровой код направления движения: 1- север, 2 - юг, 3 - восток, 4 - запад.
Построить диаграмму распределения направлений.
Отдельным столбцом для каждого из направлений отобразить факт его выбора единицей, факт невыбора - нулем. Для этого использовать логическую функцию ЕСЛИ().
Построить диаграмму индикаторов направлений.
Автосуммированием рассчитать число кварталов перемещения в каждом из направлений.
В отдельной ячейке отобразить удаленность от места побега, рассчитанную по формуле .
Повторить вычислительный эксперимент 50 раз (F9) и зафиксировать полученные удаленности R в отдельном столбце.
По данным 50 случайных событий (R) построить гистограмму распределения зоны удаления от места побега с дискретным шагом в 5 км.
Рассчитать вероятность нахождения в каждой зоне и отобразить ее графиком.
Используя электронные таблицы EXCEL, получить математические модели изменения социально-экономических процессов в Ставропольском крае.
-
Наименование
Годы
1996
1997
1998
1999
2000
Численность Мужчин, тыс.чел.
761,1
761,9
764,6
772,4
772,4
Для получения требуемых математических моделей использовать следующий алгоритм:
построить диаграмму каждого процесса;
добавить линию тренда каждого процесса;
В контекстном меню тренда каждого процесса выбрать «Формат линии тренда» и «Показывать уравнение линии тренда».
Сопоставить разные степени полиномиальных моделей.
Используя электронные таблицы EXCEL, получить математические модели изменения социально-экономических процессов в Ставропольском крае.
-
Наименование
Годы
1996
1997
1998
1999
2000
Численность Женщин, тыс.чел.
703,1
714,9
730,4
762,3
762,3
Для получения требуемых математических моделей использовать следующий алгоритм:
построить диаграмму каждого процесса;
добавить линию тренда каждого процесса;
В контекстном меню тренда каждого процесса выбрать «Формат линии тренда» и «Показывать уравнение линии тренда».
Сопоставить разные степени полиномиальных моделей.
Используя электронные таблицы EXCEL, получить математические модели изменения социально-экономических процессов в Ставропольском крае.
-
Наименование
Годы
1996
1997
1998
1999
2000
Численность населения трудоспособного возраста, тыс.чел.
1464,2
1476,8
1495
1534,7
1534,7
Для получения требуемых математических моделей использовать следующий алгоритм:
построить диаграмму каждого процесса;
добавить линию тренда каждого процесса;
В контекстном меню тренда каждого процесса выбрать «Формат линии тренда» и «Показывать уравнение линии тренда».
Сопоставить разные степени полиномиальных моделей.
Используя электронные таблицы EXCEL, получить математические модели изменения социально-экономических процессов в Ставропольском крае.
-
Наименование
Годы
1996
1997
1998
1999
2000
Среднегодовая численность занятых в экономике, тыс.чел.
1039,6
1014,2
987
1008,3
1020,5
Для получения требуемых математических моделей использовать следующий алгоритм:
построить диаграмму каждого процесса;
добавить линию тренда каждого процесса;
В контекстном меню тренда каждого процесса выбрать «Формат линии тренда» и «Показывать уравнение линии тренда».
Сопоставить разные степени полиномиальных моделей.
Используя электронные таблицы EXCEL, получить математические модели изменения социально-экономических процессов в Ставропольском крае.
-
Наименование
Годы
1996
1997
1998
1999
2000
Общая численность безработных, тыс.чел.
100
154
173
229,8
171,1
Для получения требуемых математических моделей использовать следующий алгоритм:
построить диаграмму каждого процесса;
добавить линию тренда каждого процесса;
В контекстном меню тренда каждого процесса выбрать «Формат линии тренда» и «Показывать уравнение линии тренда».
Сопоставить разные степени полиномиальных моделей.
Используя электронные таблицы EXCEL, получить математические модели изменения социально-экономических процессов в Ставропольском крае.
-
Наименование
Годы
1996
1997
1998
1999
2000
Денежные доходы населения, млн. руб.
16683,3
19346,8
20639,2
33366,9
43958,1
Для получения требуемых математических моделей использовать следующий алгоритм:
построить диаграмму каждого процесса;
добавить линию тренда каждого процесса;
В контекстном меню тренда каждого процесса выбрать «Формат линии тренда» и «Показывать уравнение линии тренда».
Сопоставить разные степени полиномиальных моделей.
Используя электронные таблицы EXCEL, получить математические модели изменения социально-экономических процессов в Ставропольском крае.
-
Наименование
Годы
1996
1997
1998
1999
2000
Численность населения, тыс.чел.
2644,6
2652,9
2659,9
2659,8
2654,2
Для получения требуемых математических моделей использовать следующий алгоритм:
построить диаграмму каждого процесса;
добавить линию тренда каждого процесса;
В контекстном меню тренда каждого процесса выбрать «Формат линии тренда» и «Показывать уравнение линии тренда».
Сопоставить разные степени полиномиальных моделей.