Уравнения Максвелла для электромагнитного поля

Введение Максвеллом понятия тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зре­ния не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.

В основе теории Максвелла лежат рассмотренные выше четыре уравнения:

1. Электрическое поле (см. § 137) может быть как потенциальным (Е_Q), так и вихревым (Е_B), поэтому напряженность суммарного поля Е = Е_Q + Е_B. Так как цир­куляция вектора Е_Q равна нулю (см. (137.3)), а циркуляция вектора Е_B определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля

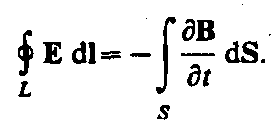
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):

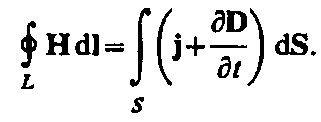
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущими­ся зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля D (см. (89.3)):

(139.1)

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плот­ностью , то формула (139.1) запишется в виде

4. Теорема Гаусса для поля В (см. (120.3)):

Итак, полная система уравнений Максвелла в интегральной форме:

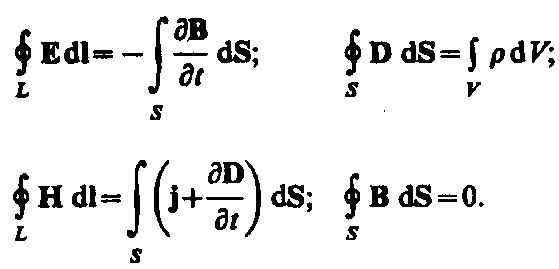
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

где ₀ и ₀ — соответственно электрическая и магнитная постоянные,  и  — соответст­венно диэлектрическая и магнитная проницаемости,  — удельная проводимость веще­ства.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Мак­свелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид

т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.

Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.

Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму допол­няют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше (см. § 90, 134):

(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).

Уравнения Максвелла — наиболее общие уравнения для электрических и магнит­ных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что перемен­ное магнитное поле всегда связано с порождаемым им электрическим полем, а пере­менное электрическое поле всегда связано с порождаемым им магнитным, т. е. элект­рическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.

Цикл Карно и его КПД. Теорема Карно

В термодинамике цикл Карно́ или процесс Карно — это обратимый круговой процесс, состоящий из двух адиабатическихи двух изотермических процессов^[1]. В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником^[2].

Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году^[3][4].

Поскольку обратимые процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному обратимому процессу Карно только с большей или меньшей степенью точности. В цикле Карно тепловая машина преобразует теплоту в работу с максимально возможным коэффициентом полезного действия из всех тепловых машин, у которых максимальная и минимальная температуры в рабочем цикле совпадают соответственно с температурами нагревателя и холодильника в цикле Карно

Пусть тепловая машина состоит из нагревателя с температурой  , холодильника с температурой   и рабочего тела.

Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах T (температура) и S (энтропия).

1. Изотермическое расширение (на рис. 1 — процесс A→Б). В начале процесса рабочее тело имеет температуру  , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты  . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.

2. Адиабатическое расширение (на рис. 1 — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника  , тело совершает механическую работу, а энтропия остаётся постоянной.

3. Изотермическое сжатие (на рис. 1 — процесс В→Г). Рабочее тело, имеющее температуру  , приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты  . Над телом совершается работа, его энтропия уменьшается.

4. Адиабатическое сжатие (на рис. 1 — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.

КПД тепловой машины Карно

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

.

Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику

.

Отсюда коэффициент полезного действия тепловой машины Карно равен

.

Теорема Карно — теорема о коэффициенте полезного действия (КПД) тепловых двигателей. Согласно этой теореме, КПД цикла Карно не зависит от природы рабочего тела и конструкции теплового двигателя и является функцией температур нагревателя и холодильника^[1].

Число степеней сво­боды. Распределение энергии по степеням свободы. Рас­пределение Максвелла. Скорости теплового движения частиц. Распределение Больцмана для частиц во внешнем потенциальном поле.

В ряде задач молекулу одноатомного газа (рис. 10, а) рассматривают как материальную точку, которой приписывают три степени свободы поступательного движения. При этом энергию вращательного движения можно не учитывать (r→0, J = mr^2→0, T_BP = Jω²/2→0). В классической механике молекула двухатомного газа в первом приближении рассматривается как совокупность двух материальных точек, жестко связанных недеформируемой связью (рис. 10, б).Эта система, кроме трех степеней свободы поступательного движения, имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси (оси, проходящей через оба атома) лишено смысла. Таким образом, двухатомный газ обладает пятью степенями свободы (i = 5). Трехатомная (рис. 10, в) и многоатомная нелинейные молекулы имеют шесть степеней свободы: три поступательных и три вращательных. Естественно, что жесткой связи между атомами не существует. Поэтому для реальных молекул необходимо учитывать также степени свободы колебательного движения.

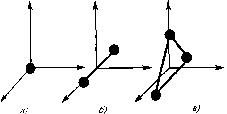
Рисунок 10 – Число степеней свободы

Независимо от общего числа степеней свободы молекул три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, поэтому на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <ε₀> в (2.13):

(2.5)

Где , П — потенциальная энергия молекулы в поле тяготения n — концентрация молекул на высоте h, n₀—то же, на высоте h = 0 , Т – температура , k-постоянная Больцмана . Выражение (2.5) называется распределением Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Применяя методы теории вероятностей, Максвелл нашел функцию f(υ) — закон о распределении молекул идеального газа по скоростям:

Теплова́я ско́рость — значение среднеквадратичной скорости теплового движения частиц.Если распределение частиц по скоростям задано некоторой функцией  , то тепловая скорость определяется как:

В случае максвелловского распределения по скоростям, определяемого температурой T, тепловая скорость равна:

где k — постоянная Больцмана, m — масса частиц. Таким образом, тепловая скорость частиц и температура вещества однозначно связаны между собой.

Электрическая емкость уединенного проводника. Конден­саторы. Емкость конденсатора. Энергия конденсатора. Энергия элек­тростатического поля. Объемная плотность энергии электростатического поля.

Рассмотрим уединенный проводник, т. е. проводник, находящийся в однородной изотропной среде вдали от других проводников и заряженных тел. При сообщении такому проводнику избыточного заряда q последний распределяется по поверхности проводника с поверхностной плотностью , которая зависит от размеров и формы проводника. Выделим на поверхности проводника малый элемент площади dS, полагая, что заряд этого элемента является точечным. В другой точке поверхности этого же проводника, отстоящей от элемента dS на расстояние r, этот заряд создает электрическое поле, потенциал которого равен

,где - относительная диэлектрическая проницаемость среды, в которой находится проводник. Интегрируя это выражение по всей поверхности проводника S, найдем потенциал, создаваемый в рассматриваемой точке всем проводником:

Так как в различных точках на поверхности проводника поверхностная плотность заряда имеет разные значения, то будем полагать, что , где k - некоторая функция координат выбранного элемента поверхности dS. Тогда выражение для потенциала проводника имеет вид

.                  (3.1)

В полученном выражении интеграл зависит от размеров и формы поверхности проводника, а также от расположения точки, для которой определяется потенциал. Значения этого интеграла не зависят от величины заряда, сообщенного проводнику, т. е. одинаковы при различных значениях заряда q. Из формулы (3.1) следует, что потенциал уединенного проводника прямо пропорционален его заряду и отношение заряда q к потенциалу для данного проводника есть величина постоянная. Это отношение называется электрической емкостью, или электроемкостью, проводника:

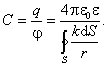
Электрическая емкость уединенного проводника зависит от его формы и размеров, а также от величины относительной диэлектрической проницаемости среды, в которой он находится. Электроемкость не зависит от материала проводника, его агрегатного состояния, от формы и размеров возможных полостей внутри проводника. Электроемкость не зависит также ни от заряда проводника, ни от его потенциала. В качестве примера найдем электроемкость уединенного проводящего шара радиуса R, покрытого слоем диэлектрика с относительной проницаемостью и толщиной d. Пусть шар имеет заряд q. Тогда напряженность поля, создаваемого шаром внутри диэлектрического слоя,

За пределами слоя напряженность поля определяется выражением:

Потенциал поверхности шара:

Таким образом, электроемкость шара, покрытого слоем диэлектрика, есть

В случае, если толщина диэлектрического слоя , емкость шара равна . При d=0 она равна . Из приведенных соотношений следует, что потенциалы одинаково заряженных и геометрически подобных проводников должны быть обратно пропорциональны их линейным размерам, а их электрические емкости прямо пропорциональны этим размерам. Электроемкость проводника численно равна заряду, который нужно сообщить этому проводнику для изменения его потенциала на единицу. В СИ единица измерения электрической емкости 1 фарада (Ф). Это емкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл: 1 Ф = 1 Кл / 1 В. Если вблизи проводника есть другие проводящие незаряженные тела, то при сообщении проводнику некоторого электрического заряда его потенциал будет меньше, чем потенциал уединенного проводника таких же формы и размеров. Это обусловлено тем, что на поверхностях тел, обращенных к заряженному проводнику, будут индуцироваться электрические заряды противоположного знака. Для наглядности поясним это явление на примере. Пусть на некотором расстоянии от проводящего шара радиуса R расположен незаряженный металлический стержень длиной l так, что его ближний конец находится на расстоянии r от центра шара, а дальний - на расстоянии (r + l). Если шару сообщить положительный электрический заряд Q, то создаваемое шаром поле будет индуцировать на ближнем конце стержня заряд -q, а на дальнем заряд +q. Потенциал шара при этом будет равен

Следовательно, электроемкость проводника возрастает, если недалеко от него находятся другие проводящие тела. В этом случае принято говорить о взаимной электроемкости проводников. Наибольший интерес представляет взаимная электроемкость системы из двух проводников с равными по величине и противоположными по знаку электрическими зарядами: |+q| = |- q| = q. Их взаимная электрическая емкость определяется как отношение заряда к разности потенциалов ,где разность потенциалов между проводниками.